基于相似度对系统循环码参数的盲识别
王兰勋,熊政达,佟婧丽
(河北大学 电子信息工程学院,河北 保定 071002)
基于相似度对系统循环码参数的盲识别
王兰勋,熊政达,佟婧丽
(河北大学 电子信息工程学院,河北 保定 071002)
针对系统循环码参数的盲识别问题,提出了一种基于数据挖掘中相似性度量函数的方法。首先,在不同的先验知识下,利用实际序列与随机序列的码重分布相似度差异最大的特性识别码长和起始点,在此基础上,通过优化传统的矩阵化简,由码字多项式与生成多项式的关系设定判定门限T的方式求解生成矩阵,实现了对系统循环码的盲识别。仿真结果表明,该算法在误码率为0.01的条件下识别效果较好。
系统循环码; 盲识别; 码重相似度; 生成矩阵
信道编码的盲识别是在未知编码信息的条件下仅根据接收到的数据快速识别编码结构,在信息截获、非协作通信、软件无线电和智能通信等领域具有广泛的应用,对该技术进行研究具有重要的价值[1-3]。
循环码被广泛应用于通信、军事等领域中,但目前,据现在公开发表的文献来看,大部分文献集中在卷积码的盲识别上,较少研究循环码的盲识别。文献[4]根据实际码重与均匀码重之间的距离估计码长;文献[5]根据比特率检测法识别码长和起始点,二者均适用低误码率的环境;文献[6]根据矩阵秩信息熵识别码长及码重信息熵识别起始点,高误码条件下识别较好;文献[7]根据欧几里德算法得到最大公因式,完成对码长及生成多项式的识别;文献[8]根据码根信息差熵和码根统计识别码长和生成多项式,二者虽容错性较好,但均只适用于本原BCH码的识别;文献[9]根据秩函数和码根特征实现循环码的盲识别,虽适用于较高的误码环境,但运算量会增加;文献[10]根据码重分布不均匀的特性识别码长和起始点,虽运算量较小,但容错性一般;文献[11]根据码重分布概率方差识别码长,计算码多项式的公约式求解生成矩阵,无复杂计算,需已知起始点。
上述的识别算法,针对性较强、计算量大或容错性一般,针对这些不足,本文提出了一种基于数据挖掘中相似度的方法进行识别,本算法无复杂计算、适用于一般循环码且容错性较好。首先,在不同的先验知识下,利用码重相似性度量函数识别码长和起始点,进而对传统矩阵进行优化来获得生成矩阵,并设置判决门限进行验证。理论分析并与其他算法进行比较,仿真结果表明,该算法在不需要大量数据截取的条件下,在高误码率为0.01时能够识别码长和起始点,且效果明显,容错性较好。
1 循环码的定义及分析
定义1[12]:设X=(x1,…,xd)和Y=(y1,…,yd)是d维空间中的两个点,相似性度量函数为Hsim(X,Y),该函数表示对象之间的相似程度,函数值越小,对象之间的差异越大,即相似性越小;相反,相似性越大。其表达式如下
(1)
定义2[13]:一个n重子空间Vn,k∈Vn,若对任何一个V=(an-1,an-2,…,a0)∈Vn,k,恒有V1=(an-2,an-3,…,a0,an-1)∈Vn,k,则称Vn,k为循环子空间或循环码。GF(q)(q为素数或素数的幂)上的[n,k]循环码中,存在唯一的n-k次多项式g(x)=xn-k+gn-k-1xn-k-1+…+g1x+g0,且每一码多项式C(x)都是g(x)的倍式,这相当于
C(x)=m(x)xn-k+r(x)=0(modg(x))
(2)
式中:m(x)=mk-1xk-1+mk-2xk-2+…+m1x+m0是信息多项式;r(x)=rn-k-1xn-k-1+…+r1x+r0是校验多项式。
定义3[13]:按照信息码元在编码后是否保持原来的形式不变,可划分为系统码和非系统码。系统码的G矩阵为G=[IK,P],左边是k×k阶单位方阵。根据生成矩阵G可以写出其校验矩阵H=[In-p,P′],其中P′是P的转置。
定义4[13]:一个码字的重量等于该码字中非零元素的个数。在二进制码中码重就是二元序列中含有“1”的个数。设Ai是[n,k,d]分组码中重量为i的码字数目,则集合{A0,A1,…,An}称为该分组码的重量分布。码重分布概率Pi是重量为i的码字个数在码字总数中出现的概率。
2 循环码的参数估计
对于循环码而言,码组内各码元之间存在较强的线性约束关系,且不同码重的码组分布是非等概率的,而对于随机序列来说,并不是任意组合的码字都会出现,根据码重分布和随机序列码重分布概率存在较大的差距进行码长和起始点的识别。

(3)
经上述分析:在起始点已知时,当码重相似性度量函数值越大,说明实际序列与随机序列越相似,差异性就越小,则该码长不是真实码长或码长的整数倍。相反,该值越小,则该码长为真实码长或码长的整数倍,即可识别码长。同理,码长已知时,起始点处对应的码重相似性度量函数值越小,即可识别起始点。
2.1 起始点为先验知识下识别码长
在实际工程中,通过帧同步信息可以找到码字的起始位置q,因此,本节已知起始点来识别码长。
已知起始点时,假设接收序列长度为N,则码长识别步骤如下:
1)初始化估计的码长为n,变化范围为1~t,t的值根据实际情况选定,将接收序列按估计码长放入矩阵中,列数为n,行数为m,且行数m=[(N-q+1)/n],即码字数,其中m>4n, 记为
Ca={c1+(m-a)n,c2+(m-a)n,…,cn+(m-a)n}
(4)
式中:a=m,m-1,…,1。
2)将每个码字Ca中的元素进行累加计算码重,即
Ha=c1+(m-a)n+c2+(m-a)n+…+cn+(m-a)n
(5)
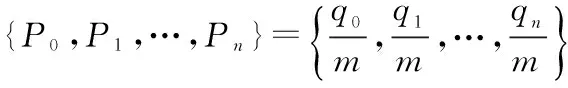
3)根据式(3)计算Hsim(P,C)的值。
4)n=n+1,转到步骤(1),计算不同码长估计值n对应的码重相似性度量函数Hsim(P,C)的值。
5)计算完成后,找出Hsim(P,C)最小值对应的码长估计值n即为真实码长。
2.2 码长为先验知识下识别起始点
码长n可以对接收的数据流处理得到,因此,识别起始点则为关键。
码长已知,则起始点识别步骤如下:
1)初始化估计的起始点为第q位,q的取值范围为1~n+1, 将接收序列N按确定的码长n放入矩阵中,列数为n,行数为m,且行数m=[(N-q+1)/n],即码字数,记为
Ca={c1+(m-a)n,c2+(m-a)n,…,cn+(m-a)n}
(6)
式中:a=m,m-1,…,1。
2)同上述码长的识别步骤2)和3)相同。
3)q=q+1,转到步骤1)继续执行,直到q=n+1,比较上述计算的结果,找出Hsim(P,C)最小值对应的q即为码字起始点。
2.3 计算生成矩阵
由码重相似性度量函数识别出码长和起始点,为达到无误码字最大化,选取在编码识别过程中出现码重概率最大的码字排列成矩阵形式,并对矩阵进行初等行变换,应采取模二运算,化简后的形式为[IkP],m-k余下行全部化为0。
求得生成矩阵G后,即可得到生成多项式,为验证其正确性,可通过式(2)来说明。当接收码字无误码时,由接收码字得到其码字多项式,并除以生成多项式,其中除法运算中减法也是模二和运算,若余式为0,则式(2)关系成立;相反,式(2)不成立。在实际噪声环境下,根据传输信道误码率设定判决门限T,当T小于式(2)成立的概率时,所得生成矩阵正确。
3 仿真验证
3.1 起始点已知,识别码长
为了验证识别方法的正确性,选取误码率Pe=0.01和Pe=0.10的(7,4)、Pe=0.01的(15,5)、Pe=0.05的(31,16)4种循环码,码元个数为104,运用MATLAB进行试验仿真,结果如图1所示。
经图1可以看出,在一定的数据量条件下,由于码组内具有完整的线性约束关系,当遍历码长为真实值或其倍数时,分组后不同码重的码字序列与随机序列码重分布概率相差较大,所以,相似性度量函数值较小,当首次出现最小值时,则为真实码长n。相反,当不是真实值或其倍数时,分组后不同码重的码字序列接近随机序列码重分布概率,所以,相似性度量函数值变化相对平稳。同时,在低误码率时,即0.001~0.010时,能正确识别码长且效果较明显,而且再次出现低值的点,可以识别2~3整数倍的码长。但随误码率的增加,虽可以明显的识别真实码长,但码长整数倍的点,识别效果不明显,可见,对于真实码长,该识别方法能适应较高的误码率,且识别效果明显。
3.2 码长已知,识别起始点
为验证识别方法的正确性,选取误码率Pe=0.05和Pe=0.1的(7,4)、Pe=0.08的(15,5)、Pe=0.03的(31,16)、Pe=0.01的(127,50)4种循环码,码元个数为104,运用MATLAB进行试验仿真,结果如图2所示。
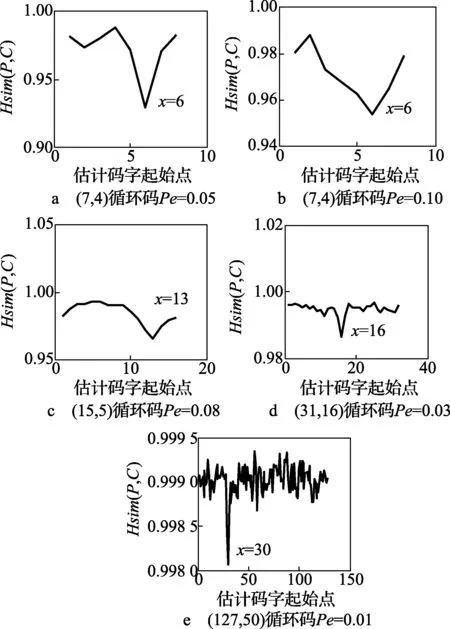
图2 码字起始点识别仿真图
经图2可以看出,码长已知,编码码字不同,所选误码率不同,依次对假设的起始点遍历,根据码重相似性函数值的大小可判断出起始点的位置。对于上述4种循环码,虽误码率不同,但都较明显的识别出起始点,可以看出,码重相似度最小值分别出现在6、13、16、30,则相似度较小,码组内线性约束关系较强,则该点即为起始点。对于(31,16)和(127,50)循环码,误码率较前者较低,由于选取码元个数相同,所以二者实验仿真所用的码字数相对于前者较少,即误码率选取要小一些,才能保证正确识别码字起始点,若要求在高误码条件下,可以选取较多的码字进行仿真即可,可见,该方法可在高误码率的条件下正确识别码字起始点,识别效果明显且容错性较好。
3.3 结果分析
在误码率Pe=0.01的条件下,选取码长与码率不同的码字进行100次蒙特卡洛仿真实验,得到不同码的正确识别概率如表1所示。
由表1可知:根据码重相似性度量函数值可以正确识别码长和起始点,但码长与码率的不同会直接影响到识别的性能。码长与码字个数相同时,低码率的码字识别效果较明显,容错性能较好,例如码长为15的码字;码长与码率相同时,选取较多的码字,码长和起始点的识别效果会有较明显的提升,例如码长为127的码字;码字个数相同,码率相近时,例如(63,24)与(127,50)两种码字,前者码长识别率高于后者。总体可得,该算法更适合于低码率的中短码进行识别。

表1 误码率Pe=0.01时识别概率
4 生成矩阵求解及验证
针对有误码的情况,选取200个码字,在含有Pe=0.015的误码条件下,以(15,5)循环码为例,利用识别码长2.1节描述中的第2)步记录码重i出现的次数记为qi,则在码字中占的概率值如图3所示。

图3 (15,5)循环码码重值分布仿真图
经图3可以看出,当码字的码重为7和8时所占概率较大,因此,选取这两种码重对应的码字构成m行n列(m>n)的矩阵,采用模二运算对矩阵进行化简,获得生成矩阵G
(7)
由循环码的定义可知,生成矩阵G的最后一行即为生成多项式的系数,即生成多项式为g(x)=x10+x8+x5+x4+x2+x+1。为检验G的正确性,可利用生成多项式g(x)来验证。首先,设置判决门限T,常规信道误码率设定为2×10-2,计算200个码字中共包含60个错误码元,设定不同码字中含有一个错误码元,计算出错误码字占所有码字的比例为30%,可得判决门限T=1-30%=70%,即当式(2)成立的概率大于T时,可认为G求解正确。在上述试验中,当n=15时,所有码字利用式(2)计算出余式为0的概率为87%,即大于70%,可见,生成矩阵G的求解正确,即可完成识别。
5 容错性比较分析
在误码条件下,对于不同参数的系统循环码,在误码率取值不同的条件下,选取2×104个码字进行1 000次蒙特卡洛仿真实验,得出码长和起始点识别率,如图4、图5所示:根据码重相似性度量函数识别码长和起始点,明显看出,(7,4)和(15,5)在误码率为0.20时,码长和起始点识别率高达95%;(31,16)在误码率为0.05时,识别率高达90%;(63,18)在误码率为0.01时,识别率高达90%。可以得出,随着循环码的码长与码率的增加,码字之间的线性约束关系降低,导致识别概率逐渐减小;同时,该算法能在高误码率条件下,能有效地识别码长和起始点。

图4 码长识别概率曲线图

图5 起始点识别概率曲线图
循环码也是一种线性分组码,分别选取2×104个4种长度的循环码为实验对象,进行仿真,图6和图7为文献[6]识别码长和起始点的概率曲线图,比较图5和图6,在码字个数与种类相同时,选取相同的起始点识别概率,可以看出,本文的误码率在高于文献[6]时,起始点仍能够正确识别。以(7,4)典型循环码为例,当起始点识别概率达到100%时,本文算法的误码率为0.15,而文献[6]的误码率为0.08,可见本文算法在识别起始点所体现出的容错性更有优势。在起始点已知时,图8为文献[11]利用码重分布概率方差识别码长概率曲线图,选取数目种类相同的码字,对文献[6,11]和本文提出的码长识别算法进行比较,图9为不同算法的90%识别误码率上限[14]曲线图,以码长15为例,本文的误码率为23%,文献[11]的误码率为8%,文献[6]的误码率为3%,仿真结果表明,在码长取值相同的条件下,本文识别算法抗误码的能力高于之前的算法,容错性较好。

图6 文献[6]起始点识别概率图

图7 文献[6]码长识别概率曲线图
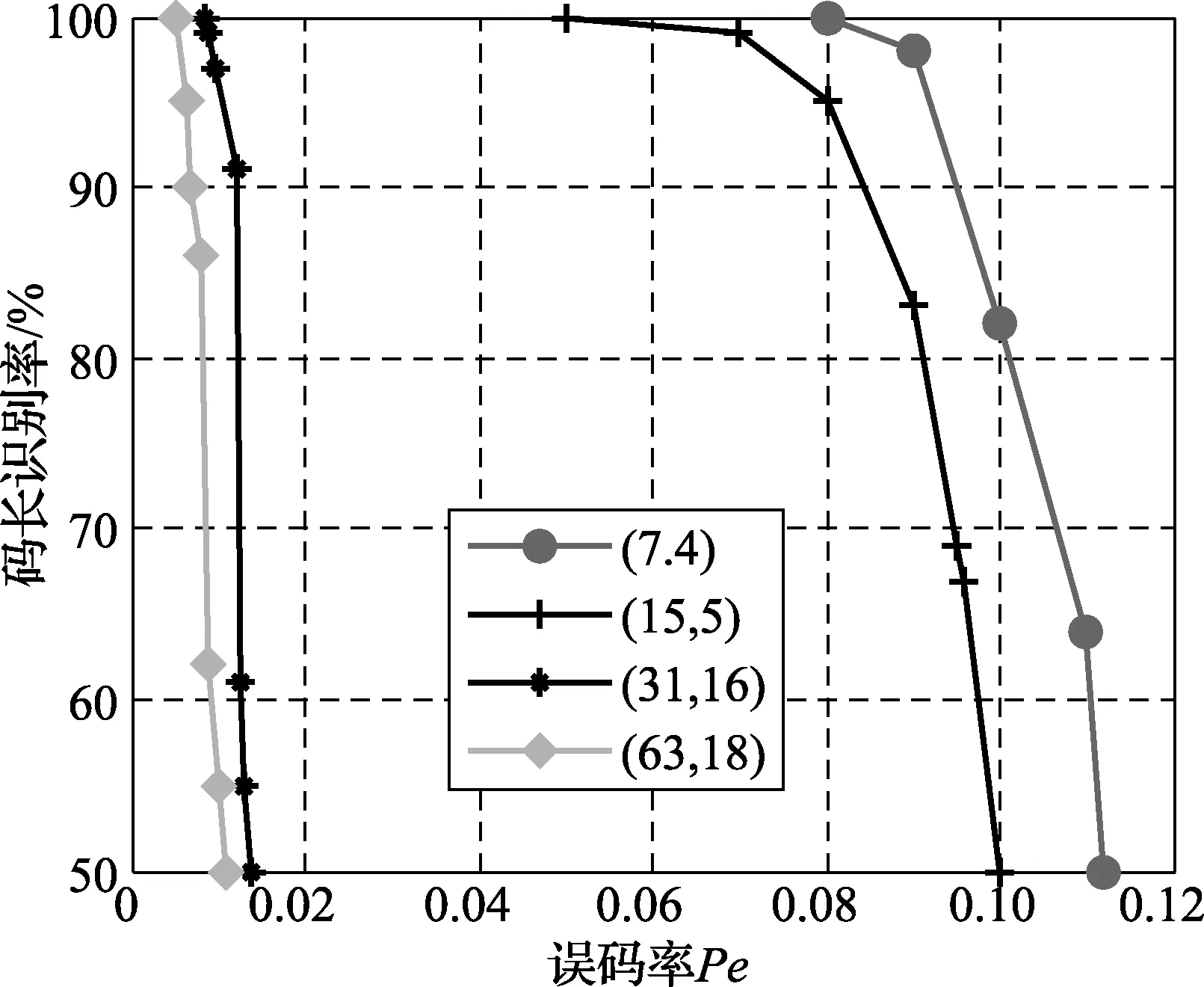
图8 文献[11]码长识别概率曲线图

图9 不同算法的90%识别误码率上限
6 结论
本文依据码重分布的特点,根据数据挖掘中相似度的方法,实现对码长和起始点的识别,在此基础上,利用优化传统的矩阵化简识别生成矩阵,即得出生成多项式,并设定判决门限完成生成多项式的正确检验,进而实现对系统循环码参数的识别。最后,在不同的先验知识和不同的误码率下,对系统循环码进行大量的仿真实验,并与其他算法进行比较,结果表明,该算法无复杂的计算,对低码率的中短码在误码率为0.01时识别效果较明显,具有较好的容错性,在增加码组数量的同时,码长和起始点的识别率得到较大的提高。
[1] 张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010.
[2] 王兰勋,佟婧丽,孟祥雅.一种线性分组码参数的盲识别方法[J].电视技术,2014,38(9):188-192.
[3] 宋镜业.信道编码识别技术研究[D].西安:西安电子科技大学,2009.
[4] 昝俊军,李艳斌.低码率二进制线性分组码的盲识别[J].无线电工程,2009,39(1):19-24.
[5] 陈金杰,杨俊安.一种对线性分组码编码参数的盲识别方法[J].电路与系统学报,2013,18(2):248-254.
[6] 陈金杰,计时钟,杨俊安.高误码条件下线性分组码的盲识别[J].应用科学学报,2013,31(5):459-467.
[7] 王兰勋,李丹芳,汪洋.二进制本原BCH码的参数盲识别[J].河北大学学报,2012,32(4):416-420.
[8] 杨晓静,闻年成.基于码根信息差熵和码根统计的BCH码识别方法[J].探测与控制学报,2010,32(3):69-73.[9] 闻年成,杨晓静.采用秩统计和码根特征的二进制循环码盲识别方法[J].电子信息对抗技术,2010,25(6):26-29.
[10] 王磊,胡以华,王勇,等.基于码重分布的系统循环码识别方法[J].计算机工程与应用,2012,48(7):150-153.
[11] 邓瑞瑞,汪立新.基于码重分布概率方差的循环码识别方法[J].太赫兹科学与电子信息学报,2013,11(5):792-796.
[12] 杨风召.高维数据挖掘技术研究[M].南京:东南大学出版社,2007.
[13] 王新梅,肖国镇.纠错码—原理与方法(修订版)[M].西安:西安电子科技大学出版社,2001.
[14] 王平,曾伟涛,陈健,等.一种利用本原元的快速RS码盲识别算法[J].西安电子科技大学学报,2013,40(1):105-110.
王兰勋(1956— ),教授,主要从事数字通信与信息编码方面研究;
熊政达(1989— ),女,硕士生,主研信道编码盲识别;
佟婧丽(1989— ),女,硕士生,主研信道编码盲识别。
责任编辑:时 雯
Blind Recognition of System Cyclic Codes Parameters Based on Similarity
WANG Lanxun,XIONG Zhengda,TONG Jingli
(CollegeofElectronicandInformationalEngineering,HebeiUniversity,HebeiBaoding071002,China)
In view of the problem of the blind recognition of system cyclic code parameters, an algorithm based on a similarity measuring function by using the method of data mining is proposed. Firstly,the code length and starting point are identified by the characteristics based on the similarity of code weight that is used by the most notable differences whose similarity of code weight distribution between the actual sequence and random sequence under the different prior knowledge.On this basis, the generator matrix is solved through the method of optimizing the traditional simplification of matrices and then employing the relationship between the code word polynomial and generating polynomial to set a decision thresholdT,the blind recognition of system cyclic code is finally realized.Simulation results show that the method has better recognition effect with BER of 0.01.
system cyclic code; blind recognition; similarity of code weight distribution; generator matrix
【本文献信息】王兰勋,熊政达,佟婧丽.基于相似度对系统循环码参数的盲识别[J].电视技术,2015,39(11).
河北省自然科学基金项目(F2014201168)
TN911.22
A
10.16280/j.videoe.2015.11.008
2014-10-25

