小角度扩展相关性近似算法分析*
李峻松,周 杰,菊池久和
0 引言
现代所讨论的多天线MIMO(Multiple Input Multiple Output)系统,不同于以前用于无线通信中传统的智能天线。智能天线的概念源于军事和声呐系统中采用的自适应阵列天线,是利用信号传输的空间特性自适应地控制波束成型,调整天线阵列的方向图跟踪强信号,减小或抵消干扰信号,提高信噪比,降低信号发射功率,提高系统容量。MIMO系统的核心是利用空时信号处理,即在原来时间维的基础上,通过使用多副天线来增加空间维,从而实现多位信号处理,获得空间复用增益或空间分集增益,因此MIMO技术可认为是智能天线技术的一种扩展,具有传统智能天线的优点[1]。因为MIMO系统的数据经过的是矩阵信道而非矢量信道,这就为改善系统性能和提高数据速率提供了更大的可能。MIMO多输入多输出系统就成了近年来在无线移动通信中的一个重大突破,在Blast实验系统、WCDMA系统、CDMA2000系统、无线城域网IEEE802.16系列以及下一代无线蜂窝系统B3G/4G系统中均已采用或计划采用MIMO多天线技术。
影响无线通信系统中信息可靠传输的主要因素,一是多径效应所引起的时延扩展,二是信道时变性所引起的频谱扩展,三是空间相关性所引起的角度扩展[2]。所有因素的限制都使得在无线衰落环境中需要付出更多的代价。研究主要谈论MIMO相关信道的物理模型和统计模型,物理模型研究中,使用的模型要反映信道中的物理散射情况[3-4],Saleh-Valenzuela模型部分基于信道物理特性,使用信号的幅度、到达时间和AOA/AOD(到达角/离开角)来表示多径分量。基于统计的信道模型并不依赖物理传播环境中特定散射情况,直接对信道参数进行建模去仿真物理信道3种小尺度衰落:时延扩展、多普勒扩展和角度扩展。对角度扩展建模的问题实际就是信道的相关性如何建模的问题。相关性系数作为天线参数的函数主要取决于到达角的功率方位谱和天线的信号发射模式[5-7]。
本论文提出一种在多天线MIMO信道相关性建模中小角度扩展近似理论算法,并应用于分析MIMO系统性能。分析中分别对高斯角能量分布、拉普拉斯角能量分布和均匀角能量分布等三种不同角能量分布情况下的空间相关性研发快速近似计算法,并同时提出双模角能量分布情况下的近似运算。通过分析这些新方法的近似效率,可以得到计算简单、复杂度低、而且符合实际的MIMO相关信道矩阵,对系统级的快速高效计算法的研究和系统级的评估以及误差分析具有重要的意义。
1 MIMO接收信号衰落相关性理论
在实际无线通信环境中,由于存在电磁波信号的反射物体,多天线MIMO系统性能受空间相关性影响较大。空间相关性计算依赖于入射信号AOA、信号功率谱结构PAS以及天线阵列单元排列结构等因素影响。本文中考虑系统模型如图1所示[8]。
再假设多路信号以某种功率谱、以一定的信号到达角到达接收天线阵,而且具有成簇特征。对于点对点单用户MIMO信道矩阵可表达为[9]

式中,Hi为N*M复高斯变量矩阵,各高斯变量具有零均值,方差为1的随机变量。Rr和Rt分别为系统接收端和发射端的信号衰落相关矩阵。如果考虑图1中线性阵列,考虑P为给定信道抽头的多径数目,()s t为接收复包络信号,gi()t为第i信道的随机衰落系数;为归一化的天线阵列间距,d为天线阵列间距,λ为波长;φ0为中心到达角。在天线阵列m单元的接收信号可表达为[10]
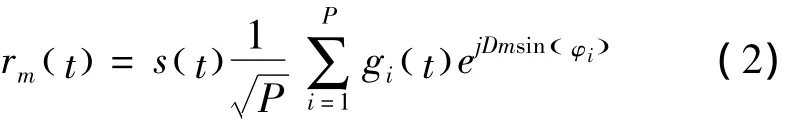
假设各到达信号角(AOA)均独立,得天线阵列单元mth与nth间的相关性可表达为[10]
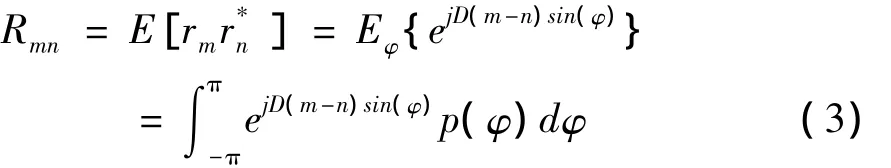
式中p(φ)为概率密度函数。

图1 线性和圆环多天线MIMO阵列结构Fig.1 Linear and circular multi- antenna MIMO array structure
本论文综合考虑均匀(Uniform)、高斯(Gaussian)和拉普拉斯(Laplacian)分布,在前人的大量研究基础上,进一步深入全面研究空间相关性精确和近似算法、MIMO信道建模以及算法精确度评估。
考虑相关函数的拉普拉斯分布为[6]

把式(4)代入相关性计算式(3)中,经过推导、整理,可得拉普拉斯分布条件下的相关性系数Rmn精确计算式如下[11]:

式中Jk为k阶第一类贝塞尔函数。
类似地,考虑相关函数的高斯分布、均匀分布分布为[6,9]:

其中 θ∈ [φ0-Δ,φ0+Δ ]。把式(6)(7)代入式(3)中,计算得出两种分布下相关性系数Rmn的精确计算式。
高斯分布下:
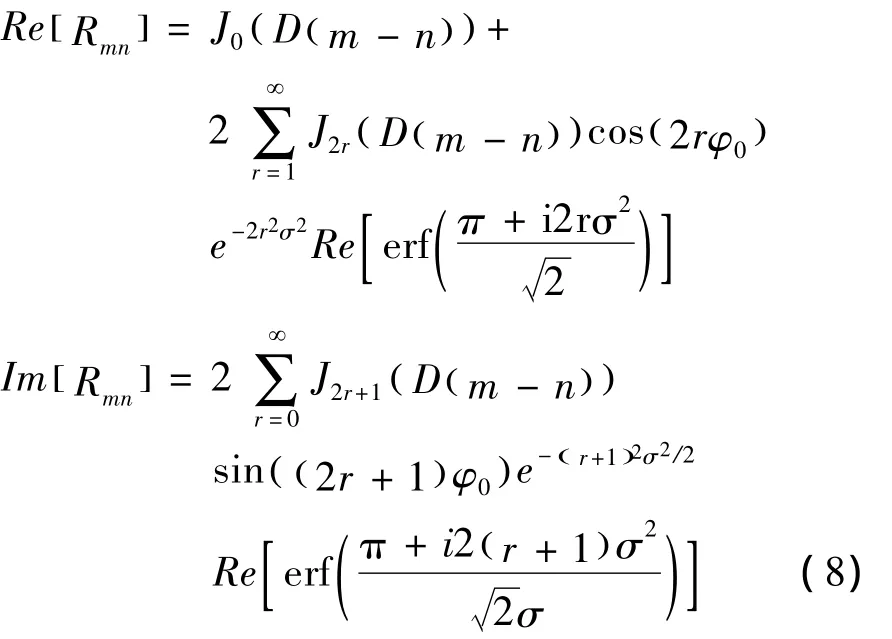
均匀分布下:


图2 不同分布下空间相关性精确结果随间距波长比d/λ变化情况(σ =15°,φ0=45°)Fig.2 Exact spatial correlations versus ratio of distance to wavelength with different distributions(σ =15°,φ0=45°)
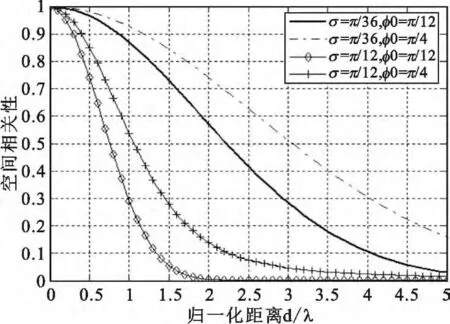
图3 不同系数的高斯分布下空间相关性精确结果随间距波长比变化情况Fig.3 Exact spatial correlations versus ratio of distance to wavelength with Gaussian distribution
图2 为在 σ =15°,φ0=45°时不同分布下空间相关性精确结果随间距波长比d/λ变化情况,可以看出高斯分布条件下较为乐观(较低的相关性)。同时由图3可以看出,在相同距离和AOA条件下,σ越小,空间相关性越高;相同距离和σ条件下,AOA越大,空间相关性越高。这一特性同样适用于其他分布情况下[12]。
2 MIMO衰落相关性近似算法
各分布下相关性的精确计算式(5)(8)(9)显得复杂,要获得精度较高的结果,累加技术须取得较大。为控制和降低计算复杂度,获得较好的近似结果,可在Δ取较小时的情况下,采取近似算法对式(5)(8)(9)进行化简,简化算法复杂度、提高算法精度,以及对后续MIMO性能评价影响都值得研究和探讨,结果对MIMO信道建模与系统性能仿真都具有重要的意义。
在角度扩展角Δ较小的情况下,可使用近似式cosΔ=0、sinΔ=Δ。拉普拉斯分布情况下,把该近似式代入式(5),再对其化简整理,相关性系统Rmn可得

如果再从相关性系数定义式(3)来看,在Δ较小时,拉普拉斯分布域为[-π,π]间,参考文献[13],经推导简化,相关性系数表达式(5)可简化为

同理对高斯分布和均匀分布情况下的相关性系数计算公式进行简化,可得
高斯分布下:

均匀分布下:

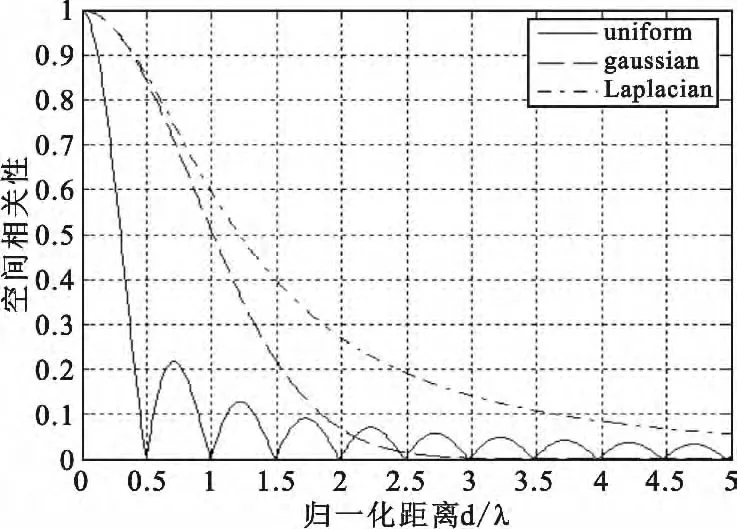
图4 不同分布下空间相关性近似结果随间距波长比变化情况(σ =15°,φ0=45°)Fig.4 Approximate spatial correlations versus ratio of distance to wavelength with different distributions(σ =15°,φ0=45°)
图4 为在 σ =15°,φ0=45°时不同分布下空间相关性近似结果随间距波长比d/λ变化情况,与图2显示的相关性精确结果相对比,误差的变化显示在图5中。由图5可见高斯分布和拉普拉斯分布下的相关性近似计算具有良好的相似性,能得到误差较小的结果。而均匀分布下的近似计算由于三角函数特性所产生的振荡,导致在距离较大时才能得到相对精确的近似值。不同的角度扩展和AOA情况下近似效率也有所区别。由于近似的条件是小角度扩展情况下,所以当角度扩展增大时近似效率会显著降低,同时AOA的增大也会导致近似效率的下降,这一点在图6中体现了出来。
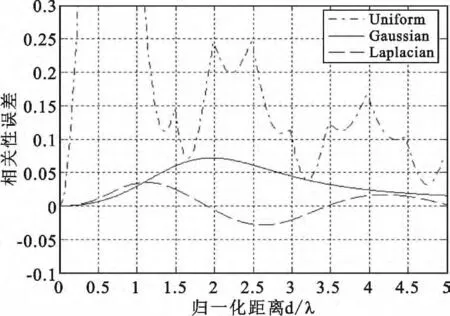
图5 不同分布下空间相关性近似结果与精确值间的误差变化情况(σ =15°,φ0=45°)Fig.5 Deviations between exact and approximate spatial correlations with different distributions(σ =15°,φ0=45°)

图6 不同系数的高斯分布下相关性近似结果与精确值间的误差变化情况Fig.6 Deviations between exact and approximate spatial correlations with Gaussian distribution
3 双模分布情况及近似算法
实际情况中MIMO信道常为多簇的情况,因此角分布可能为多模的情况。在此我们考虑双模分布下的相关性计算及其近似算法。
首先设角能量分布为两个拉普拉斯分布的叠加[14],即


其中φ1、φ2分别为两个独立分布的中心到达角。在Δ较小时,经推导计算得
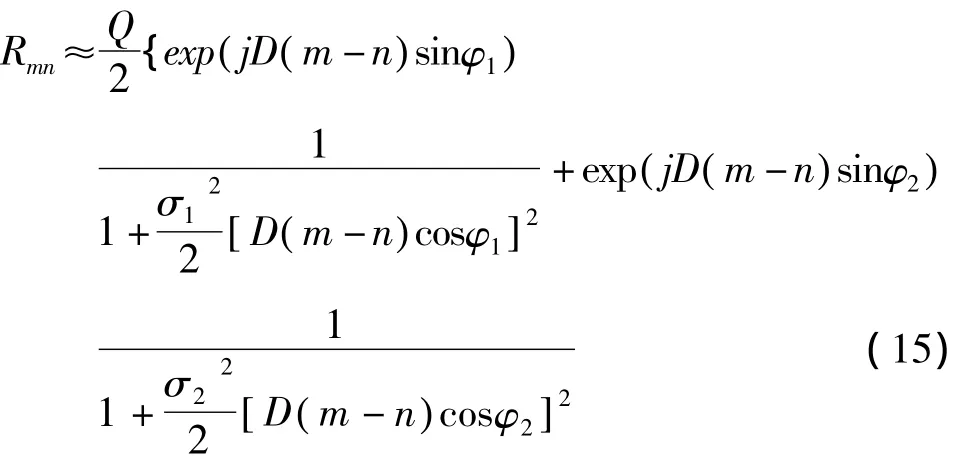
类似的,可以推导得到高斯、均匀双模分布下的相关性近似公式:
高斯双模分布下:
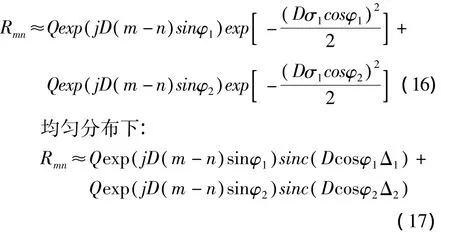
图7是双模分布下空间相关性近似结果与精确值间的误差变化情况,因为相关方程与受到由于与另一分布的中心到达角不同而产生振荡的单模分布情况十分类似,故误差变化情况也与图5所显示的类似。此外通过仿真得出当两簇AOA相近时,振荡幅度小,近似效率较高;反之则近似效率较低[14]。

图7 双模分布下空间相关性近似结果与精确值间的误差变化情况 (σ1=15°,φ1=45°;σ2=10°,φ2=15°)Fig.7 Deviations between exact and approximate spatial correlations with different bi-modal distributions(σ1=15°,φ1=45°;σ2=10°,φ2=15°)
4 MIMO衰落信道遍历容量分析
信道遍历容量是按照所有的信道实现平均化后的最大可传输速率,它只取决于MIMO多天线信道矩阵 ^H的分布情况。为达到由遍历容量所得速率,要求发送端在功率约束的条件下优化信道协方差矩阵,结合式(1)则可得遍历容量为[15]

其中Rx为输入协方差矩阵,Tr( Rx)为协方差矩阵Rx的迹;ρ为发送信号信噪比,B为信道带宽,IM为M维单位矩阵,M是用户端天线阵列单元数。为使信道遍历容量最大化,最优的策略是将功率平均分配到每个发送天线上,即遍历容量最大化的输入协方差矩阵为,其中S为基站天线阵列单元数。此时信道遍历容量为[15]

图8为在σ=15°,φ0=45°时不同分布下遍历容量随间距波长比d/λ变化情况,图中Uniapx,Gauapx,Lapapx分别表示均匀分布、高斯分布和拉普拉斯分布的近似情况。由图中可以看出,信道遍历容量随空间相关性的降低而增大,当空间相关性趋近于0时遍历容量达到最大。在各分布情况下容量大小相差极小,且高斯分布和拉普拉斯分布的近似计算具有非常好的效率。均匀分布的近似在距离较近时会有较大的误差,该误差随着距离的增大而减小,最后与精确结果趋于一致。

图8 不同分布下遍历容量随间距波长比d/λ变化情况(σ =15°,φ0=45°,ρ=10dB)Fig.8 Ergodic capacity versus ratio of distance to wavelength d/λ in different distributions(σ =15°,φ0=45°,ρ=10 dB)
5 结语
本文本论文提出一种在多天线MIMO信道相关性建模中小角度扩展近似理论算法,通过运算评估了不同角分布条件下的近似效率。该算法在高斯分布、拉普拉斯分布下具有良好的近似性,近似误差不超过±0.1。均匀分布下由于函数的振荡特性导致结果并不理想。近似效率受角度扩展和中心到达角的共同影响,随角扩展和中心到达角的扩大而降低。双模分布下的相关性近似效率亦受到双簇不同的中心到达角AOA影响,当其相近时近似误差较小,反之较大。衰落信道遍历容量随着天线阵列单元间距的增大而减小,在空间相关性趋于0时达到最大。仿真结果显示本算法在信道容量估计上具有非常好的近似精确度,有效拓展了空间相关性计算及其对MIMO信道影响的研究。
[1] CHANDRAN S.Adaptive Antenna Arrays:Trends and Applications[M].Berlin:Springer- Verlag Berlin and Heidelberg GmbH & Co.K,2004:43-44.
[2] ZHOU J,SASAKI S,MURAMATSU S,et al.Spatial Correlation for a Circular Antenna Array and Its Applications in Wireless Communications[J].IEEE GLOBECOM,2003(2):1108-1113.
[3] LOYKA S,MOSIG J.ChannelCapacity of N - antenna BLAST Architecture[J].Electronics Letters,2000,36(7):660-661.
[4] TSAIJA,BUEHRERRM,WOERNERBD.SpatialFading Correlation Function of Circular Antenna Arrays with Laplacian Energy Distribution[J].IEEE Communications Letters,2002,6(5):178 -180.
[5] LEE W C Y.Effects onCorrelation between Two Mobile Radio Base - station Antennas[J].Communications,IEEE Transactions on,1973,21(11):1214 -1224.
[6] SALZ J,WINTERSJ H.Effect ofFading Correlation on A-daptive Arrays in Digital Mobile Radio[J].Vehicular Technology,IEEE Transactions on,1994,43(4):1049 -1057.
[7] TSAI J A,WOERNER B D.The Fading Correlation Function of a Circular Antenna Array in Mobile Radio Environment[C]//Global Telecommunications Conference,2001.San Antonio:IEEE,2001(5):3232-3236.
[8] FORENZA A,HEATH R W.Benefit of Pattern Diversity via Two-element Array of Circular Patch Antennas in Indoor Clustered MIMO Channels[J].Communications,IEEE Transactions on,2006,54(5):943-954.
[9] 张唯希,周杰.基于相关矩阵的MIMO系统信道容量分析[J].通信技术,2011(3):132-135.
ZHANG W,ZHOU J.Analysis on Channel Capacity of MIMO Architecture based on Correlation Matrix[J].Communications Technology,2011(3):132 -135.
[10] FORENZA A,LOVE D J,HEATH R W.ALow Complexity Algorithm to Simulate the Spatial Covariance Matrix for Clustered MIMO Channel Models[C]//Vehicular Technology Conference,2004.Washington:IEEE,2004(2):889-893.
[11] SCHUMACHER L,PEDERSEN K I,MOGENSEN PE.From Antenna Spacings to Theoretical Capacitiesguidelines for Simulating MIMO Systems[C] //Personal,Indoor and Mobile Radio Communications,2002.Lisboa:IEEE,2002(2):587-592.
[12] BHAGAVATULA R,HEATH R W.Computing theReceive Spatial Correlation for a Multi-cluster MIMO Channel Using Different Array Configurations[C] //Global Telecommunications Conference,2008.New Orleans:IEEE,2008:1-5.
[13] FORENZA A,LOVE D J,HEATH R W.Simplified Spatial Correlation Models For Clustered MIMO Channels with Different Array Configurations[J].Vehicular Technology,IEEE Transactions on,2007,56(4):1924-1934.
[14] BUEHRER R M.The Impact of Angular Energy Distribution on Spatial Correlation[C]//Vehicular Technology Conference,2002. Proceedings. Vancouver:IEEE,2002(2):1173-1177.
[15] GOLDSMITH A.无线通信[M].杨鸿文,李卫东,郭文斌,等译.北京:人民邮电出版社,2007:273-280.GOLDSMITH A.WirelessCommunication[M].YANG H,LI W,GUO W,et al.Beijing:Posts& Telecom Press,2007:273 -280.

