基于模拟退火粒子群优化的恒模算法*

孔珊珊，李秀霞

0 引言

在短波信道中，由于各种复杂因素导致信号在接收端会产生严重的码间干扰。码间干扰现象严重影响了短波通信系统的性能，造成极高的误码率，使接收端无法接收正确的信号，而均衡技术是消除码间干扰问题的重要手段。传统的自适应均衡技术的实现首先需要周期性地发送已知的训练序列，根据已发送的训练序列来调节均衡参数，之后再发送信息序列。短波信道是一个时变突发性强的信道，要实现短波信道的均衡需要及时并频繁的发送已知的训练序列，可见传统的自适应均衡算法已经不能满足短波信道均衡的需要。而盲均衡技术不需要训练序列只依靠接受序列本身的特性就可获得与信道相匹配的参数，实现信道补偿，因此盲均衡技术能够很好完成短波信道的均衡。恒模算法(Constant Modulus Algorithm，CMA)［1－2］是最常用的一种盲均衡算法。恒模盲均衡算法由于具有计算简单、收敛性好、易于实时实现、有效性高等优点，被广泛应用于多种通信系统中。

对于传统的CMA算法，存在收敛速度和剩余误差之间的矛盾，即步长大，则收敛速度快，但稳态剩余误差大;步长小，则收敛速度慢，但稳态剩余误差小［3］。针对这一矛盾，本文提出一种步长随着误差和迭代次数而变化的CMA算法。粒子群优化算法(PSO)是基于群体智能理论的优化算法，通过种群中粒子间的合作与竞争产生的群体智能指导优化搜索，收敛速度较快［4］。为了进一步加快算法的收敛速度，本文利用PSO算法对均衡器的权向量进行优化。但是PSO算法在寻优的过程中容易陷入局部最优，针对PSO优化算法的这一特点，引入模拟退火算法［5－6］(Simulated Annealing，SA)，SA 算法不仅能接收好的解，而且还能够接收不好的解，是一种具有很强的概率突跳能力的算法，在寻优过程中能够避免陷入局部极小值。SA算法和PSO算法相结合，能够增强算法的搜索能力，提高算法的收敛速度。

1 恒模盲均衡算法

Bussgang类盲均衡算法的核心是构建一个代价函数和一个非线性控制函数，然后利用某种算法寻找目标函数的最小值。不同的Bussgang算法对应不同的无记忆非线性函数。Bussgang类盲均衡器的原理框图［7］如图1所示。

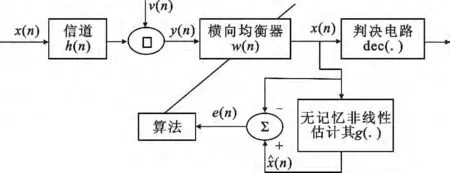
图1 Bussgang类盲均器的原理框图Fig．1 Bussgang blind equalizer diagram

图1 中，x(n)代表输入信号，v(n)代表噪声信号，h(n)代表基带信道的冲击响应，y(n)代表均衡器的输入，˜x(n)代表均衡器的输出，^x(n)代表估计信号，dec(．)代表量化判决装置，e(n)为˜x(n)和^x(n)之间的误差，g(．)代表无记忆非线性函数。Bussgang盲均衡器采用一个无记忆非线性估计函数g(．)，尽可能使^x(n)=g［˜x(n)］成立。

Bussgang类盲均衡算法的权系数迭代公式为:式(1)中，μ表示步长因子，一般μ取足够小的正常数。CMA的代价函数为:

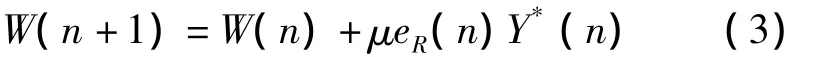
CMA的权系数迭代公式为:由式(3)可知，固定步长μ是CMA的影响参数。当步长取不同值时，算法的收敛性能不同，步长是影响CMA性能的重要指标。当步长μ取值较大的时候，收敛速度快，但均方误差大;当步长μ取值较小的时候，收敛速度慢，但均方误差小。因此可以得出，固定步长的CMA在收敛速度和稳态剩余误差之间存在着矛盾，从而影响CMA的性能。

2 基于SAPSO优化的变步长CMA算法

2． 1 变步长CMA算法的提出

利用变步长代替固定步长，能够克服传统CMA算法在收敛速度和收敛精度之间的矛盾，提高均衡性能。变步长CMA算法的基本思想是在算法迭代的初期阶段采用较大的步长，加快收敛速度，等到算法收敛后，采用较小的步长，降低稳态剩余误差，提高算法的性能［8］。

为了解决步长变化的问题，本文构建了基于误差信号和迭代次数的变步长CMA算法。基于误差信号的CMA算法的步长随着误差信号的变化而变化，误差信号的大小在收敛的条件下随着迭代次数的增加而减小，通过误差信号控制步长因子;基于迭代次数的CMA的步长随着迭代次数的增加而逐渐减小，将误差信号和迭代次数综合起来控制步长因子，可以很好地解决算法在开始收敛阶段和收敛后所需步长的要求，进而提高算法的性能［9－10］。其变步长公式为:

式(4)中，μ代表步长因子，参数n代表算法的迭代次数，参数 α、β、ρ、k1、k2k3、c 均为步长的调整因子。当迭代次数n大于0小于等于50时，步长采用公式(5)，即基于迭代次数的变步长;当迭代次数n大于等于50时，步长采用公式(6)，即基于误差函数的变步长。

此时CMA的权向量更新公式为:

同时，为了确保算法具有良好的收敛性和稳健性，步长因子必须满足:

式(8)中，R为均衡器输入信号的自相关矩阵，tr(R)为自相关矩阵的迹。步长因子在调整的过程中必须满足(8)，否则，不予处理，直接进行下一步迭代。

2． 2 SAPSO优化的CMA

基于误差和迭代次数的CMA算法只是对步长进行了改进，为了进一步提高此算法的性能，考虑利用均衡器的权向量因素对均衡器的权向量进行优化。PSO算法是一种基于迭代的优化工具，能够全方位的搜索最优解是解决最优问题的智能算法。利用PSO算法对变步长CMA算法的权向量进行初始化，以找到最优的初始化权向量加快算法的收敛速度。但是PSO算法具有易陷入局部最优的缺点，并且在收敛后期收敛速度变慢，收敛的精度变差。因此我们将SA算法引入到PSO算法中，SA算法具有很好的突跳能力，可以避免粒子群陷入局部最优［11－12］。将SA算法和PSO算法结合起来使用，不仅能够加强CMA算法的寻优能力，而且还克服了算法在搜索过程中陷入局部极值的缺陷。

设随机产生的初始化粒子群中每一个粒子作为均衡器的一个权向量，以变步长恒模算法的代价函数的倒数作为模拟退火粒子群算法的适应度函数。基于SAPSO优化的变步长CMA算法的具体操作步骤如下:

Step1:随机初始化种群中各粒子的位置和速度分别为:

Step2:记录当前各个粒子的位置和适应度值个体极值pbest，即pi，并记整个种群中全局最优解pg;

Step3:确定初始温度t0

Step4:根据下列公式确定当前温度下各pi所对应的是配置:

Step5:使用轮盘赌策略从所有的个体极值中寻找全局最优的替代值pg，然后用以下两个公式更新粒子的速度和位置:

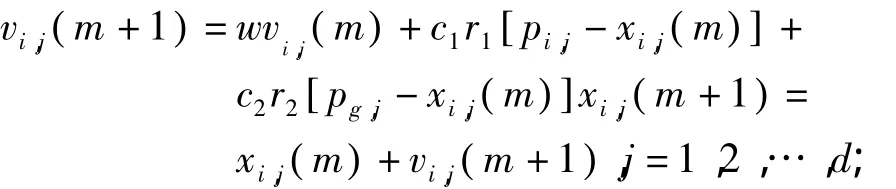
Step6:确定各粒子的目标值，记录各粒子的pi和pg;

Step7:退温;

Step8:如果满足所解决问题的调件则停止搜索。

步骤Step1到Step8中，c1、c2和w算法的参数，其中c1和c2是学习因子，w是惯性权重。通过不断更新其个体极值和全局极值的位置，找到最大的适应度值，最大适应度值所对应的权向量就是变步长CMA算法的最优的权向量，将最优化的权向量作为基于模拟退火的粒子群优化的变步长CMA算法的初始权向量。

3 实验仿真及分析

基于Watterson短波信道模型环境下验证本文提出算法的有效性，利用MATLAB的Simulink模块建立Watterson短波信道模型如图2所示。

图2 Watterson等效短波信道模型Fig．2 An equivalent Watterson HF channel model

设置滤波器有11个抽头，多普勒扩展取为10 Hz，输入信噪比为50 dB。从图2产生的信号供M文件应用。模拟退火算法中初始温度的选择和退温方式的设定对算法具有不可忽略的作用。在此选择初始温度为t0=f(pg)/ln5，退火的方式设置为t=t+lamda，其中lamda为退火常数。从图2产生的信号供M文件应用，经过短波信道以后的输出信号作为均衡器的输入，对此信号进行均衡。经过多次的仿真实验，当新算法的主要参数设置适当时(如表1)，算法的均衡性能达到最好。

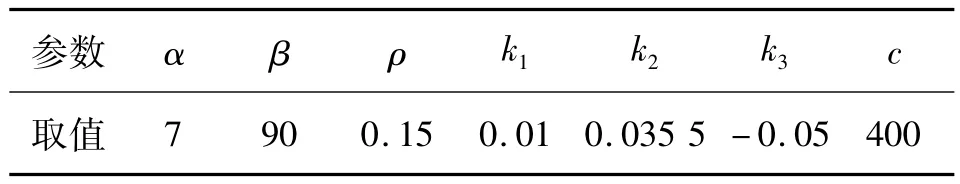
表1 主要参数的取值Table 1 Value of the Main Parameters

在上面环境的下，得到固定步长的CMA算法(μ=0．05)、本文提出的变步长 CMA算法和基于SAPSO优化的变步长CMA算法的收敛曲线图见图3。

图3 三种算法的算法收敛曲线Fig．3 Convergence curve of the three algorithms

从图3中我们可以明显的看出，在收敛速度近乎相同的情况下，变步长CMA收敛后的均方误差明显低于传统的CMA算法的均方误差;基于SAPSO优化的变步长CMA算法与变步长CMA算法相比，不仅收敛后的均方误差降低，而且加快了收敛速度，在迭代前几次的时候就开始收敛并且趋于稳定。各种算法的均衡性能详见表2。

由表2可看出，加粗字体的数值都要比没加粗字体的数值小，说明在同一迭代次数下，变步长CMA和基于SAPSO优化的CMA的均方误差都要比出传统CMA的均方误差低;在第10次迭代时，基于SAPSO优化的CMA算法的均方误差也明显低于变步长CMA算法的均方误差，并且可以看出基于SAPSO优化的变步长CMA算法的均方误差从10次迭代就近乎趋于稳定，并且明显低于前两种算法的数值。

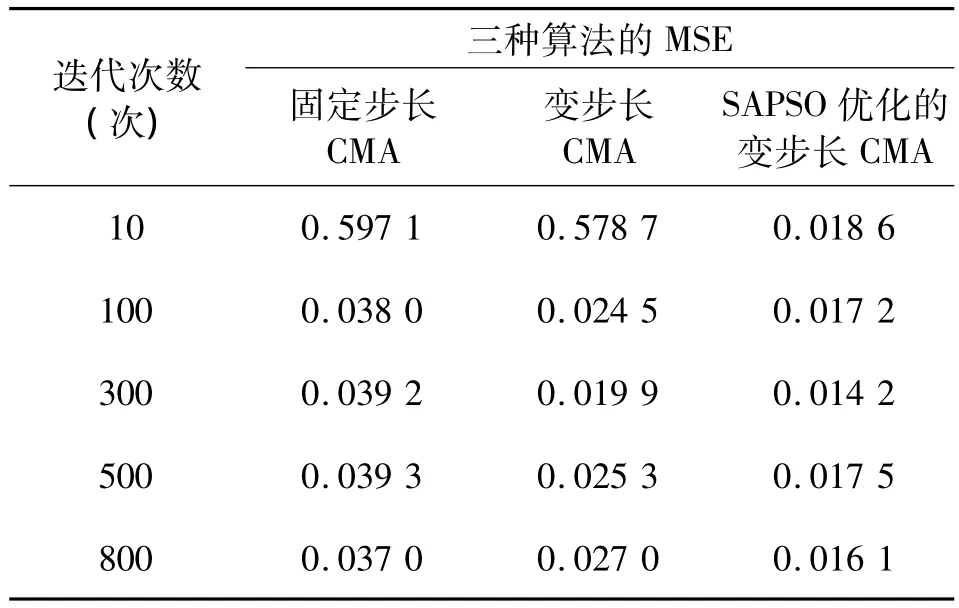
表2 迭代次数所对应三种算法的均方误差Table 2 Three algorithms corresponding to mean square error table based on the number of iterations

综合图3、和表2考虑，可以得出，变步长CMA算法和基于SAPSO优化的变步长CMA算法的性能都优越于传统的CMA的性能，其中，利用SAPSO算法优化后的变步长CMA算法的均衡效果最好。通过大量的实验验证了本文所提出的两种算法的有效性。

4 结语

恒模算法是通信系统中最为广泛采用的盲均衡算法，由于其收敛速度和收敛精度之间存在相互制约的缺点，使得它的均衡性能受到限制。变步长CMA算法，解决了收敛速度和收敛精度之间的矛盾。本文构建了基于迭代次数和误差信号相结合的变步长 CMA，并且将SAPSO算法引入到变步长CMA。通过 MATLAB软件对提出的两种算法在Watterson短波信道中进行了仿真验证，对比分析:变步长CMA算法和基于SAPSO优化的变步长CMA算法的均衡性能都明显优于传统的CMA盲均衡算法。

［1］ GODARD D N．Self－Recovering Equalization and Carrier Tracking in Two－dimensional Data Communication Systems［J］．IEEE Trans Commun，1980，28(11):1867 －1875．

［2］ TREICHIA R JR，AGEE B．A New Approach to Multipath Correction of Constant Modulus Signals［J］．IEEE Trans ASSP，1983，31(2):459－471．

［3］ 蔡理金．CMA算法盲均衡性能分析［J］．通信技术．2011，12(44):19－23．

CAI Li－jin．Analysis on Blind Equalization Performance of CMA Algorithm［J］．Communications Technology．2011，12(44):19－23．

［4］ 刘衍民．粒子群算法的研究及应用［D］．济南:山东师范大学，2011．

LIU Yan－ min．Research of Particle Swarm Optimization and Its Application［D］．Jinan:Shandong Normal University，2012

［5］ 高鹰，谢胜利．基于模拟退火的粒子群优化算法［J］．计算机工程与应用．2004，(1):47－50．

GAO Ying，XIE Sheng － li．Particle Swarm Optimization Algorithms Based on Simulated Annealing［J］．Computer Engineering and Applications．2004，(1):47－50．

［6］ 刘汉婕．基于模拟退火的粒子群改进算法的研究与应用［D］．北京:华北电力大学，2012．

LIU Han－jie．Research andApplication of Modified Particle Swarm Optimization Algorithms based on Simulated Annealing［D］．Beijing:North China Electric Power University，2012．

［7］ 岳蕾．Bussgang类盲均衡算法研究［D］．西安:长安大学，2008．

YUE Lei．Bussgang Blind Equalization Algorithm ［D］．Xi'an:Chang'an University，2008．

［8］ 高丽娟，赵洪利，蒋太杰．一种改进的变步长常模算法［J］．电子与信息学报．2007，29(2):283－286．

GAO Li－ juan，ZHAO Hong － li，JIANG Tai－ jie．A Modified Variable Step Size Constant Modulus Algorithm［J］．Journal of Electronics ＆ Information Technology．2007，29(2):283－286．

［9］ 孙俊香，赵继印．基于迭代次数变步长的LMS算法在

ECG信号提取中的应用［J］．现代商贸工业．2007，19(11):280－282．

SUN Jun－xiang，ZHAOJi－yin．Application of the ECG Signal Extraction Based on the Number of Iterations Variable Step－size LMSAlgorithm［J］．Modern Commerce Industry．2007，19(11):280－282．

［10］ 于霞，刘建昌，李鸿儒，一种变步长凸组合自适应滤波器及其均方性能分析［J］．2010．38(2):280－284．

YU Xia，LIU Jian － chang，LI Hongru．A Convex Combination of Variable Step－size Adaptive Filter and Its Mean － Square Performance Analysis［J］．2010．38(2):280－284．

［11］ 龚纯，王正林．精通MATLAB最优化计算［M］．电子工业出版社．2012:270－309．

GONG Chun，WANG Zheng － lin．Proficient MATLAB Optimization Calculation［J］．Publishing House of Electronics Industry．2012:270－309．

［12］ 刘志峰，杨德军，顾国刚．基于模拟退火粒子群优化算法的拆卸序列规划［J］合 肥 工 业 大 学 学 报．2012．32(2):161－166．

LIU Zhi－feng，YANG De－jun，GU Guo－gang．Disassembly Sequence Planning Based on Particle Swarm－Simulated Annealing Optimization［J］．Journal of Hefei University of Technology．2012．32(2):161 －166．