基于层次分析法的矿井六大系统模糊综合评价

李宁，王李管，贾明涛



基于层次分析法的矿井六大系统模糊综合评价

李宁1, 2, 3，王李管1, 2, 3，贾明涛1, 2, 3

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；2. 中南大学 数字矿山研究中心，湖南 长沙，410083；3. 长沙迪迈数码科技股份有限公司，湖南 长沙，410083)

为了对矿井六大系统进行合理有效的评价，首先利用层次分析法建立六大系统多层次评价指标体系，借助两两比较法和标度法构建相应因素的比较判断矩阵并计算各因素的权重向量，再根据模糊数学理论并按照评价结果划分的级别分别确定连续型指标和离散型指标的隶属度，最后通过建立模糊综合评价模型，实现对矿井六大系统的综合评价。研究结果表明：运用该方法在某矿山对已建成的六大系统进行综合评价，评价结果为良好，能够准确、客观地反映六大系统的建设情况。

矿井六大系统；层次分析法；判断矩阵；模糊数学理论；综合评价

为了使矿山企业安全生产工作得到进一步加强，企业的安全生产水平得到全面提升，金属非金属地下矿山企业必须建设安全避险“六大系统”[1−2]。随着矿山企业六大系统建设的逐步完善，对所建系统进行合理有效的评价显得尤为重要。六大系统的综合评价是一个多层次、多因素、多目标和多指标的分析过程，由于缺少各子系统建设完善程度和各子系统间关联性的定量评估，从而构成了六大系统综合评价的技术难点[3−4]。目前，大多数矿山企业对六大系统综合评价方法没有考虑各子系统间的关联性和复杂性，同时缺少相关的理论依据，导致评价结果具有盲目性和主观性。针对上述问题，本文作者首先借助层次分析法[5−8]，在深入分析六大系统综合评价影响因素的基础上建立六大系统综合评价指标体系，用两两比较法和标度法客观的确定各影响因素的权重，再根据模糊数学理论[9]，对矿井六大系统进行综合评价。

1 六大系统多层次评价指标体系

1.1 六大系统

金属非金属地下矿山安全避险六大系统[10]是国家安全生产监督管理总局为了实现生产调度统一指挥，生产效率得到提高，及时排除安全隐患，要求所有金属非金属地下矿山企业必须建设完善的井下监测监控系统、人员定位系统、紧急避险系统、压风自救系统、供水施救系统和通信联络系统，简称六大系统。

1.2 评价指标体系的建立

六大系统的综合评价是一个复杂的系统工程，必须对影响六大系统的各个因素进行深入分析，建立合理的评价指标体系是进行科学、有效评价的前提。

层次分析法[11−13]首先将分析对象的因素建立起彼此相关的递阶层次结构，清晰地反映出各相关因素之间的关系，可以利用较少的定性和定量的信息使决策过程数学化，从而使六大系统的综合评价问题简化。按照层次分析法的分层原则，同时根据影响六大系统综合评价的各类因素和国家规范，将金属、非金属地下矿山安全避险六大系统综合评价指标体系划分为3层，其结构如图1所示，从左到右依次是目标层、因素层和因子层。在该层次结构中，右边一层元素对其相关的左边一层元素的影响就是该右边一层元素对其相关左边一层元素的权重。

gi为一级因素层；gij为二级因素层(；)

由图1可以得出：在评价指标体系中，定量化与定性化因素同时存在，并且相互影响。通过层次分析法建立综合评价指标体系后，需对体系中各因素进行量化[14]。六大系统的综合评价结果划分为3个级别：优秀、良好和及格，分别用I，II和III表示。根据国家规范及相关专家的经验，可确定图1所列23项因素对六大系统综合评判影响的界限值。但是每种因素所表示的物理意义不相同，在进行模糊综合评价之前，需对原始数据进行处理，形成标准化的数据，如表1所示。

表1 评价指标分级标准表

1.3 评价指标权重向量的确定

1.3.1 构造比较判断矩阵

为了确定各因素的权重向量，采用两两比较的方法，根据比较结果建立相应的比较判断矩阵。两两比较法[15]的具体方法是：假设以上一层次某个元素作为比较准则，用一个比较标度u来表示本层次中第个元素与第个元素的相对重要性。u的取值一般为整数1~9及其倒数，其取值规则如表2所示。

表2 元素uij取值规则

根据层次分析法，建立的比较判断矩阵为

1.3.2 求解评价指标权重向量

考虑到在生成比较判断矩阵时是定性比较量化的结果，不需要进行精确计算，因此，只需采用简便的方法计算比较判断矩阵的最大特征值max和所对应的排序向量(即权重向量)。本文采用和法[16]进行计算，其步骤如下。

1) 将判断矩阵的列向量进行归一化处理：

4) 计算比较判断矩阵的最大特征根：

1.3.3 比较判断矩阵的一致性检验[17]

两两比较法具有较大的主观性，完全根据专家的经验和知识来进行判断，可能会出现不一致的情况，故需要对判断矩阵进行一致性检验。判断矩阵一致性检验的公式为

式中：C为不一致程度的量化指标；为比较判断矩阵的阶数；I为平均随机一致性指标，通过统计计算给出了I取值，见表3。

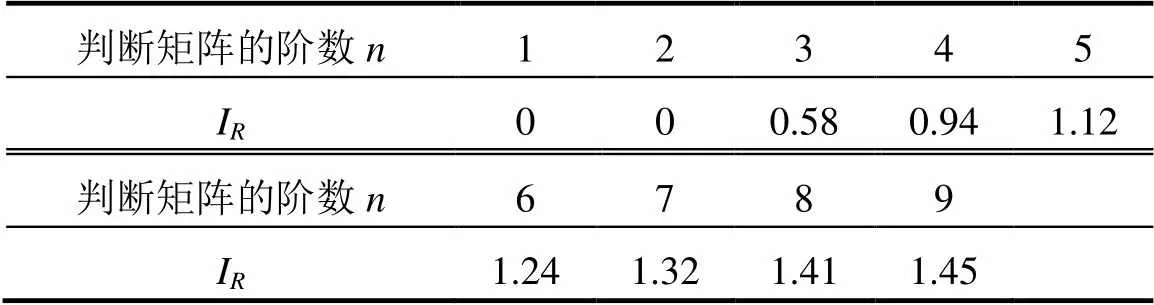
表3 平均随机一致性指标取值

当C＜0.1时，可以认为判断矩阵的一致性是满足要求的，否则应对判断矩阵重新调整，直至满足一致性检验标准为止。通过运用上述方法进行计算，得到六大系统综合评价体系中各因素和因子的权重如表4所示。

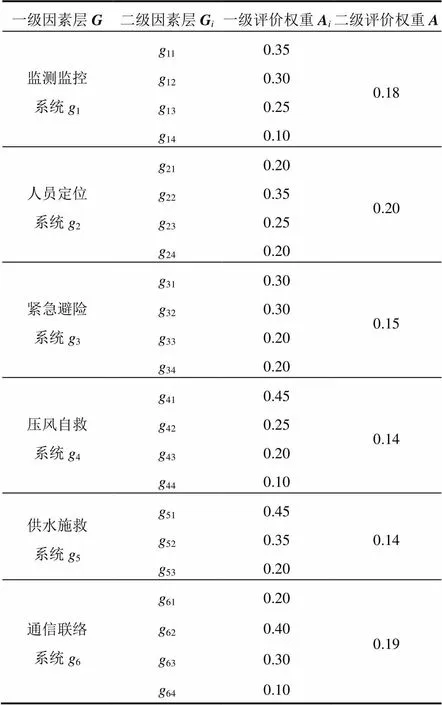
表4 评价指标两级权重分配表

2 六大系统模糊综合评价

2.1 评价指标隶属度的确定

由图1可知：影响六大系统综合评价的因素可分为定性和定量两类，前者属于离散型变量，后者属于连续型变量。根据确定隶属度的基本原则，本文采用德菲尔法[9]和公式法分别建立离散型变量和连续型变量的隶属度函数。对于表1中离散型变量，根据德菲尔法确定隶属度，见表5。而对于连续型变量，其隶属度则通过与影响因素之间建立函数关系来求取。隶属函数种类较多，通过分析各影响因素的模糊分布特征，采用如下公式计算各因素的隶属度。

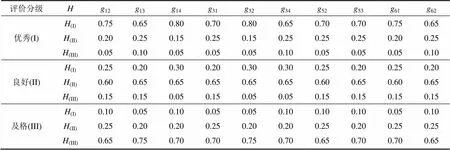
表5 离散型因素隶属度取值

1) 偏小型：

2) 中间型：

3) 偏大型：

式中：为定量因素标准化后的数值；1，2和3分别为相应定量因素在综合评价结果为优秀、良好和及格时的标准化数值。

2.2 模糊综合评价模型的建立

评价对象的一级因素集、二级因素集及对应的权重向量、和评价集分别为：

2.2.1 第二级因素集G模糊评价矩阵的确定

将影响六大系统综合评价因素进行归类，定量因素将其标准化的值代入隶属函数中，确定隶属度；定性因素按照表5确定相关隶属度，从而求得单因素的评价矩阵为

2.2.2 一级模糊综合评价

选用加权平均型运算模型进行计算，得单因素评价向量[9,16]为

2.2.3 二级模糊综合评价

通过一级综合评价，得到单因素评价向量，将其组合可得二级综合评价矩阵。同样选用加权平均型运算模型进行计算，得二级综合评价向量，即

再根据得到的二级综合评价向量，按贴近度原则进行评价，确定六大系统综合评价结果。

2.3 模糊综合评价流程

六大系统综合评价的具体流程如下：

1) 利用层次分析法建立六大系统多层次评价指标体系；

2) 确定各因素对六大系统综合评判影响的界限值；

3) 通过运用两两比较法和标度法确定评价指标(影响因素)权重向量并做一致性检验；

4) 分别采用德菲尔法和公式法确定评价指标的隶属度；

5) 根据建立的模糊综合评价模型对六大系统进行综合评价，确定六大系统的综合评价级别。

3 工程实例应用

以建成六大系统的某矿山为例，对六大系统进行综合评价，综合评价指标体系各元素量化值见表6。

表6 评价指标元素量化表

3.1 一级模糊综合评价

根据表6，对于离散型因素，参照表5确定对应因素的隶属度；对于连续型因素，将其标准化值代入式(7)，(8)和(9)确定各单因素分别对I，II和III级六大系统的隶属度。

监测监控系统的评价矩阵为

再由表4可知，权重向量1=(0.35，0.30，0.25，0.10)，从而得到单因素评价向量1=11=(0.404，0.521，0.075)。

人员定位系统的评价矩阵为

再由表4可知，权重向量2=(0.20，0.35，0.25，0.20)，

从而得到单因素评价向量2=22=(0.477 5，0.436 5，0.086 0)。

紧急避险系统的评价矩阵为

由表4可知，权重向量3=(0.30，0.30，0.20，0.20)，从而得到单因素评价向量3=33=(0.52，0.28，0.20)。

压风自救系统的评价矩阵为

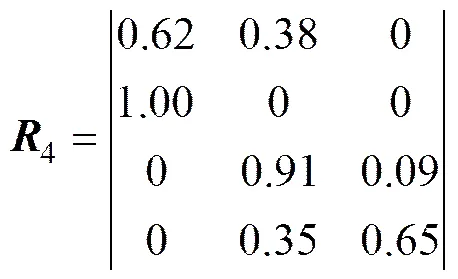
由表4可知，权重向量4=(0.45，0.25，0.20，0.10)，从而得到单因素评价向量4=44=(0.529，0.388，0.083)。

供水施救系统的评价矩阵为

由表4可知，权重向量5=(0.45，0.35，0.20)，从而得到单因素评价向量5=55=(0.438 0，0.515 4，0.047 5)。

通信联络系统的评价矩阵为

由表4可知，权重向量6=(0.20，0.40，0.30，0.10)，从而得到单因素评价向量6=66=(0.294，0.616，0.090)。

3.2 二级模糊综合评价

通过一级模糊综合评价可得二级模糊评价矩阵：

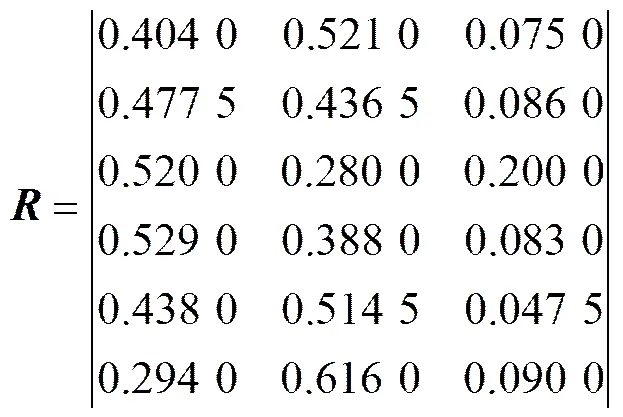
由表4可知，权重向量=(0.18，0.20，0.15，0.14，0.14，0.19)，从而得到二级综合评价向量==(0.437 5，0.466 5，0.096 0)。

根据二级模糊综合评价向量知，该矿所建六大系统属于II的隶属度最大。按照贴近度原则，该矿所建六大系统的综合评价结果为良好，评判结果与实际情况相符。

4 结论

1) 利用层次分析法建立六大系统多层次模糊综合评价指标体系，再根据两两比较法和标度法构建比较判断矩阵，确定评价指标的权重向量并进行一致性检验，确保得到合理的权重向量。

2) 根据建立的模糊综合评价指标体系，利用德菲尔法和公式法计算评价指标的隶属度，分别对一级因素集和二级因素集进行模糊综合评价并得到相应的综合评价向量，再按贴近度原则确定六大系统评价结果。

3) 采用层次分析法和模糊数学理论对矿井六大系统进行综合评价，克服了现有评价方法的盲目性，具有坚实的理论基础，矿山的实际运用表明评价结果准确可靠。

[1] 国务院关于进一步加强企业安全生产工作的通知(国发[2010]23号)[EB/OL]. http://baike.baidu.com/view/4001617.hem, 2010−09−10.
State Administration State Council Concerning Further Reinforce Work Safety in Enterprise (State Issue [2010] No. 23)[EB/OL]. 2010−09−10. http://baike.baidu.com/view/ 4001617.hem

[2] 孙继平. 煤矿井下安全避险“六大系统”的作用和配置方案[J]. 工矿自动化, 2010(11): 1−4.
SUN Jiping. Effect and configuration of “Six Systems” for safe act of rescue of coal mine underground[J]. Industry and Mine Automation, 2010(11): 1−4.

[3] 吴凤东, 胡乃联, 王长龙. 基于未确知测度理论的煤矿井下“六大系统”安全评价模型[J]. 煤炭学报, 2011, 36(10): 1731−1735.
WU Fengdong, HU Nailian, WANG Changlong. Safety evaluation model of “Six System” in coal mine underground based on the unascertained measure theory[J]. Journal of China Coal Society, 2011, 36(10): 1731−1735.

[4] 卢国志, 李希常, 方永焱. 煤矿安全指标评价体系研究及应用[J]. 安全与环境学报, 2003, 3(3): 29−31.
LU Guozhi, LI Xichang, FANG Yongyan. Study and establishment of safety assessment index system colliery[J]. Journal of Safety and Environment, 2003, 3(3): 29−31.

[5] 曹文贵, 张永杰. 地下结构岩体质量分类的变权重二级模糊综合评判方法研究[J]. 岩石力学与工程学报, 2006, 25(8): 1612−1618.
CAO Wengui, ZHANG Yongjie. Study on two-stage fuzzy synthetic judgment method with changing weight value for rock quality classification in underground structures[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(8): 1612−1618.

[6] 郭湛, 商小雷, 李海. 基于AHP的轨道交通安全评价体系模型[J]. 中国铁道科学, 2011, 32(3): 123−125.
GUO Zhan, SHANG Xiaolei, LI Hai. AHP-based safety assessment model for rail transit system[J]. China Railway Science, 2011, 32(3): 123−125.

[7] 王新民, 赵彬, 张钦礼. 基于层次分析和模糊数学的采矿方法选择[J]. 中南大学学报(自然科学版), 2008, 39(5): 875−880.
WANG Xinmin, ZHAO Bin, ZHANG Qinli. Mining method choice based on AHP and fuzzy mathematics[J] Journal of Central South University (Science and Technology), 2008, 39(5): 875−880.

[8] 丁丽宏. 基于改进的灰关联分析和层次分析法的边坡稳定性研究[J]. 岩土力学, 2011, 32(11): 3431−3441.
DING Lihong. Research on estimation of slope stability based on improved grey correlation analysis and analytic hierarchy process[J]. Rock and Soil Mechanics, 2011, 32(11): 3431−3441.

[9] 杨纶标, 高英仪. 模糊数学原理及应用[M]. 4版. 广州: 华南理工大学出版社, 2006: 45−68.
YANG Lunbiao, GAO Yingyi. Theory and applications of fuzzy mathematics[M]. 4th ed. Guangzhou: South China University of Technology Press, 2006: 45−68.

[10] 丰建荣, 史鹏飞, 代贵生. 煤矿井下安全六大系统可靠性分析[J]. 太原理工大学学报, 2011, 42(6): 625−627.
FENG Jianrong, SHI Pengfei, DAI Guisheng. Analysis on the reliability of the six systems for coal mine underground danger prevention[J]. Journal of Taiyuan University of Technology, 2011, 42(6): 625−627.

[11] WANG Y M, ELAHG T M S. An approach to avoiding rank reversal in AHP[J]. Decision Support System, 2006, 42(3): 1474−1480.

[12] Stam A, Duarte Silva A P. On multiplicative priority rating methods for the AHP[J]. European Journal of Operational Research, 2003, 145(1): 92−108.

[13] Scholl A, Manthey L, Helm R, et al. Solving multiattribute design problems with analytic hierarchy process and conjoint analysis: An empirical comparison[J]. European Journal of Operational Research, 2005, 164(3): 760−777.

[14] Ramanathan R. Data envelopment analysis for weight derivation and aggregation in the analytic hierarchy process[J]. Computers & Operations Research, 2006, 33(5): 1289−1307

[15] 李凤伟, 杜修力, 张明聚, 等. 改进的层次分析法在明挖地铁车站施工风险辨识中的应用[J]. 北京工业大学学报, 2012, 38(2): 165−172.
LI Fengwei, DU Xiuli, ZHANG Mingju, et al. Application of improved AHP in risk identification during open-cut construction of a subway station[J]. Journal of Beijing University of Technology, 2012, 38(2): 165−172.

[16] 吴启红, 彭振斌, 陈科平, 等. 矿山采空区稳定性二级模糊综合评判[J]. 中南大学学报(自然科学版), 2010, 41(2): 661−667.
WU Qihong, PENG Zhenbin, CHEN Keping, et al. Synthetic judgment on two-stage fuzzy of stability of mine gob area[J]. Journal of Central South University (Science and Technology), 2010, 41(2): 661−667.

[17] Saaty T L. Decision making with dependence and feedback: the analytic network process[M]. Pittsburgh: RWS Publications, 2001: 225−279.

An analytic hierarchy process based fuzzy evaluation of underground mine six-system

LI Ning1, 2, 3, WANG Liguan1, 2, 3, JIA Mingtao1, 2, 3

(1. School of Resource and Safety Engineering, Central South University, Changsha 410083, China;2. Digital Mine Research Center, Central South University, Changsha 410083, China;3.Changsha Digital Mine Co. Ltd., Changsha 410083, China)

A multi-layer evaluation index system was established via the analytic hierarchy process for the mine six-system to evaluate the mine six-system effectively. By applying the comparative method and the scale method, the comparative and determining matrix and the weight for all the matrix elements were made. The mathematical fuzzy theory and the evaluated result were then used to respectively figure out determining degree of membership for continuous indexes and discrete indexes. Finally, a general fuzzy evaluation model was built to conduct a comprehensive evaluation of the six-system. The application of this method in a production mine shows that construction of the six-system is satisfactory and conforms to the actual situation.

mine six-system; analytic hierarchy process; comparative matrix; fuzzy mathematics theory; comprehensive evaluation

TD79

A

1672−7207(2015)02−0631−07

2014−03−12；

2014−06−20

国家高技术研究发展计划(863计划)项目(2011AA060407)(Project (2011AA060407) supported by the National Science and Technology Research and Development Program (863 Program))

李宁，博士研究生，从事数字矿山及智能采矿技术研究；E-mail：13875910191@163.com

10.11817/j.issn.1672-7207.2015.02.035

(编辑 赵俊)