基于改进遗传算法下的数字信号特征值调制识别

王　孟，蔡明辉

（国家无线电监测中心乌鲁木齐监测站，乌鲁木齐　830054）

基于改进遗传算法下的数字信号特征值调制识别

王孟，蔡明辉

（国家无线电监测中心乌鲁木齐监测站，乌鲁木齐830054）

通信信号的调制识别及调制参数特征值的估计是信号处理领域的一个重要研究方向。本文在改进遗传算法的基础上，首先确定最能表现信号调制差别的特征值集合，将该集合作为最优秀基因库，然后在遗传的演化过程中通过选择、交叉、淘汰引起的优秀基因库的变化，遗传过程中引入竞争惩罚策略引起基因库的优化，保证每代都是高质量的基因。

遗传算法；特征值提取；调制识别；惩罚竞争

1　引言

在数字信号调制识别过程中，文献［1］提出利用数字统计模式识别方法将各种不同的信号调制类型的区分。该方法主要从特征量的提取和特征集选择、分类器对不同类型调制边界划分两个方面讲述不同信号的调制类型。但在对特征量提取方面人的主观性对数据提取带来影响。为了克服主观性对信号特征量和特征集的选择，文献［2］提出用遗传方法对特征量和特征集进行筛选。但由于传统的遗传算法收敛速度慢，容易产生局部收敛，局部搜索能力差等缺陷，文献［3］对遗传算法进行改进，在传统遗传算法的基础上，引入相关联赛选择和相关家庭竞争两个算子，采用自适应策略惩罚进化过程中的违约个体，解决遗传算法和局部搜索能力弱的缺陷。但这些改进后的算法设计复杂，遗传多样性，造成局部搜索过程中产生局部收敛。

本文针对数字信号特征集选择问题，提出一种新的改进的遗传算法，该方法从每一代的物种中找出优秀的基因，确保基因库基因的质量。下一代的遗传由该基因库中的基因组成，通过选择、剔除，从而改变基因库的大小，然后引进其他种群中的优质基因，是变异达到优质的多样性。最后将该方法用在对数字信号调制的MFSK的识别。

2　遗传算法

2.1遗传算法的简介

简单遗传算法（GA）已经被用在通信信号特征值的选取［6］。但由于其内部结构和机制因素，造成简单遗传算法存在局部搜索和收敛能力弱的缺陷，难以确保选择出最优子集。遗传进化选择过程中，物种个体多样性及个体选择压力是两个相互制约的因素。因此采用合适的选择压力，保持物种个体的多样性，是提高遗传算法性能的关键。

2.2遗传算法的性能估计

定义1：设Xc（s）为环境c下策略s的在线性能，fc（t）为第t代相应于环境c的目标函数或均方根适应度函数，则Xc（s）可以表示为

该式表明，在线性能可以用于第一代到当前代的优化过程的均方根值来表示。

定义2：设X'c（s）为环境c下的策略s离线性能，则有

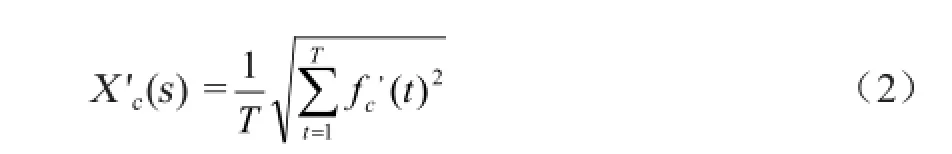
式中，f'c（t）为smart｛fc（1），fc（2），fc（3）…fc（t）｝。式（2）表示离线性能是特定时刻最佳适应度的均方根值。

3　改进遗传算法

改进遗传算法是在分析简单遗传算法的基础上，引入相关竞赛选择（CFS）和相关家族竞争（CMS）两个算子，利用选择淘汰来引起优秀种群大小变化，然后引入库外基因，从而优化交叉变异概率。此方法在满足变异收敛性的同时，其多样性化不至于收敛过快。

CFS和CMS的核心在一定范围内，以个体适应度和个体汉明距离为依据，经过选择参与、相互交叉进入下一代的个体。此方法适用于信号解调识别特征向量选取中，由于每个特征向量在被信号识别中都含了一定的信息量，因此，可将每个特征向量看成一个遗传基因，将所有特征向量集合认为成基因库（G），每组特征的组合看成一条染色体，从而找出能表征识别出信号的染色体。

3.1相关竞赛交叉选择

（1）在祖父辈中的个体任意选取一个单体S0，作为参与交叉选择的一个祖父代个体。

（2）从种群S（n）中随意取m个个体构建竞争群体，即

（3）评估S中所有个个体的相互关联函数，即

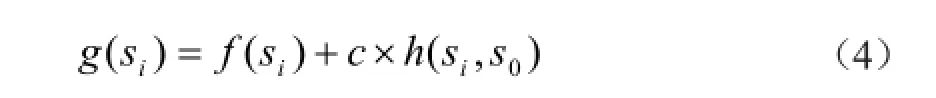
式中，f（si）是第i个个体的适应度值；h（si，s0）是竞争团体中的个体si与s0的汉明距离；c是相互关联的权重。

（4）从s中选取对应g（si）值最大的个体作为另一个交叉祖父代的个体。

3.2相关家竞争（CMS）

（1）从参与竞争的祖父代和产生的父代中选出适应度最高的个体x。

（2）计算x与另外5个个体yi（i=1，2，3，4，5）的汉明距离di（i=1，2，3，4，5）。

（3）从di中选取最大的dj=max（di）。

（4）确定yj为优胜个体，与个体xi一起进入下一代。

3.3改进遗传因子惩罚约束法

遗传算法在运行过程中，遗传因子的作用是能产生解也有可能不能产生解，因此需要对不能产生解的采取约束处理。改进遗传因子惩罚函数法的核心和难点是选取遗传因子惩罚函数和系数以避免过惩罚和欠惩罚。本文遗传算法可根据个体违约程度信息自动调整遗传因子惩罚函数。根据文献［4］中基于遗传因子约束法如下：

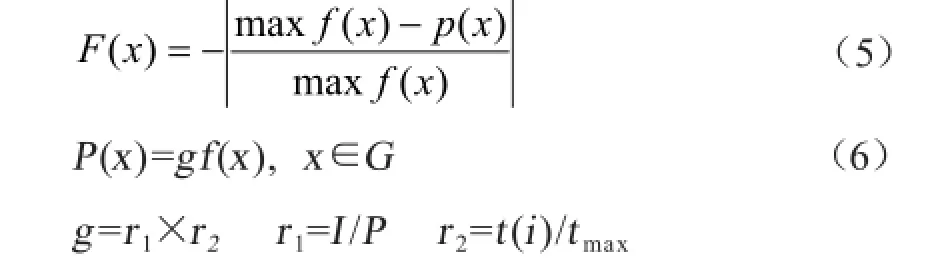
式中，f（x）表示个体适应度函数；P（x）表示遗传因子惩罚函数；G表示可行域；g是惩罚系数；r1表示种群不可行率；r2表示种群中最大违约值的比值；I表示种群中不可行解的个数；P表示种群大小；ti表示种群中第i个不可行解的违约值；tmax表示种最大不可行违约值。

3.3改进遗传算法的流程

（1）确定编码策略，用编码位串法表示需求解参数。

（2）设定种群规模大小，最大遗传代数，交叉概率和变异几率，并用随机法生成初始种群。

（3）计算每个种群的个体的适应度，并根据该值的大小选择操作，适应度比较大的个体可能被选中，而适应度小的个体可能经过限制约束被淘汰。

（4）用交叉、变异和遗传因子约束法作用于被选中的个体，生成新一代的个体。

（5）将重复运行（2）、（3）和（4）直到满足终止条件。

（6）输出最优解。

4　算法的实现与测试

4.1特征值选择与描述

对于数字信号解调过程中特征值的选择就是对0-1的规划，目标函数为：

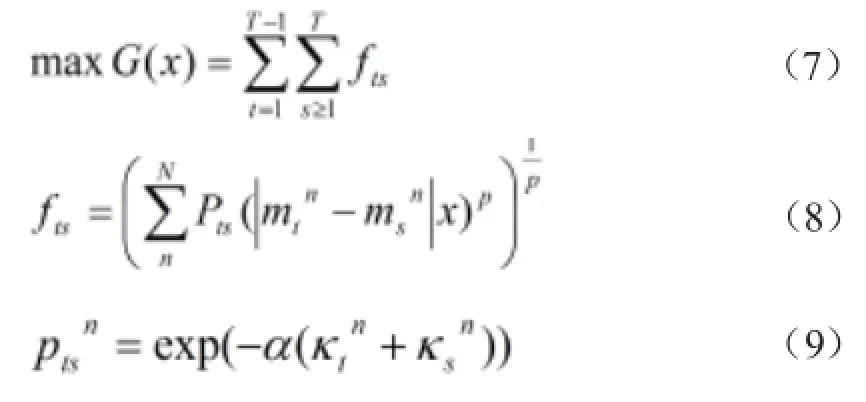
惩罚约束条件为

式中，p≤1；α＞0；K表示需要识别的数字信号；mt，ms分别为类型σt，σs均方根特征向量；kt，ks分别为σt，σs的绝对值方差向量；N表示初始特征向量的维数；G表示子集特征向量的维数。

4.2信号特征值的初始化

本文根据已调制信号的特征类型组成的集合PSK，2PSK，MSK，4ASK，4FSK，16QAM，DQPSK，DPSK信号类型。

在适应度的选择和计算上，选取RBF神经网作为识别率计算器，计算遗传因子中染色体的识别率。采用码元速率分别为2k，2.5k，3k和3.5k，单位为band，载频为2500Hz，2650Hz，2800Hz，3000Hz共四组，采样频率为24kH，4FSK最大频率偏移为800Hz，切为连续相位调制，幅度调制信号基带成余弦滚降系数α=0.5，信噪比为15dB。

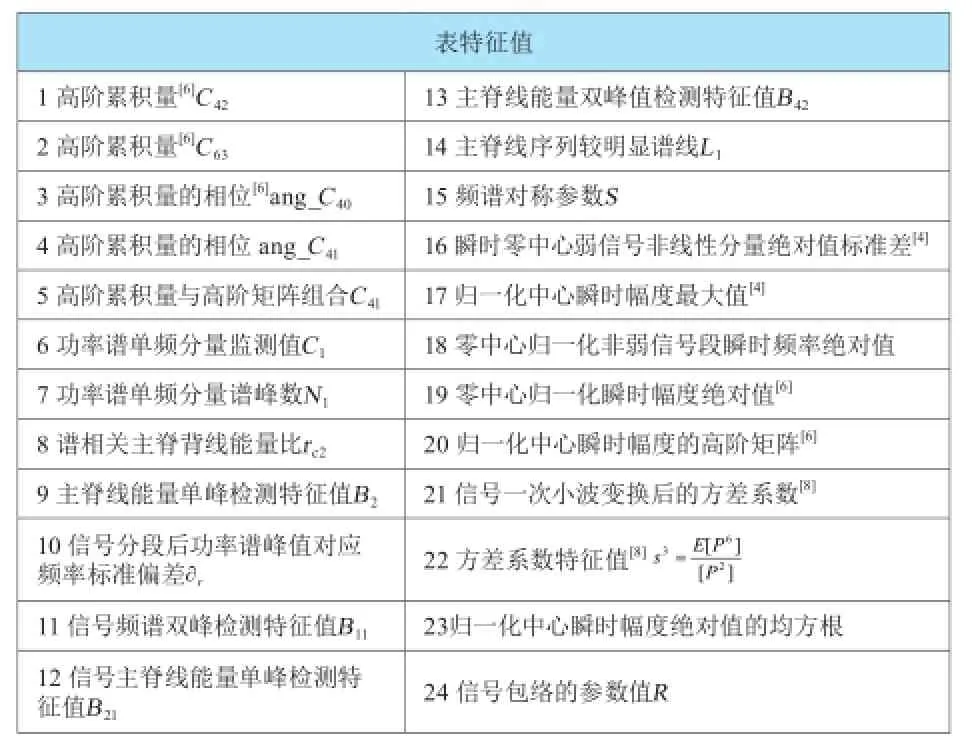
表1　初始特征值

4.3改进遗传算法结果分析

最优秀的特征子集大小定位8，从24个特征值中选出8个特征。在设定数据大小相同的状况下，算法30次重复运行。

遗传代数80代，种群大小N=80，初始化概率p=0.3参数设置：16进制编码，加入联赛竞争的参数T=3，相关距离权重C=3。

图1为本文所实现的遗传算法和改进遗传算法的比较。图1a可以看出本文所实现的遗传算法随着遗传代数的增加，收敛性越好，遗传基因的多样性也越来越好。图1b为最有适应度的仿真曲线，从图中可以看到本文实现的算法和改进遗传算法具有好的收敛速度，并且收敛到合适的值。

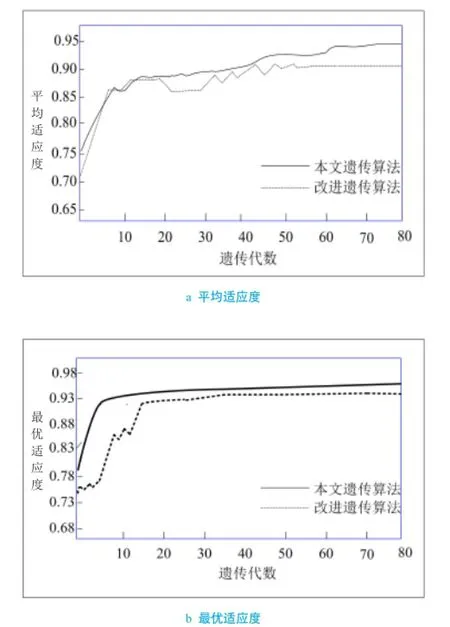
图1　适应度曲线比较

5　结束语

相关竞争惩罚和相关联赛选择两个算子合理的分配和协调种群个体的多样性和选择压力，解决了改进遗传算法中对特征向量的随机选择。此方法在与改进遗传算法中增加竞争惩处参数的限制，对全局有更好收敛性和更快的收敛速度，对数字信号调制的识别和解调是很有效的。

［1］吕铁军，王珂，肖先赐.新特征选择方法下的信号调制识别［J］.电子与信息学报，2006，2（5）:661-666

［2］Du Zhuoming， Feng ing.Support vector machine feature selection algorithm based on modified genetic algorithm［J］.Computer En-gineering and Applications， 2009， 45（ 29） : 28-30

［3］Wang Keqi，Yang Shaochun，Dai Taihong，etal，Method of optimizing parameter of least squarers support vector machines by genetic alogorithm ［J］Computer Applications and software 2009，7（26）:109-111

［4］赵丽娜，刘培玉，朱振方.自适应遗传算法在特征选择中的改进及应用［J］.计算机工程与应用，2009， 45（7）:39-64

［5］Yang Hong，Lu Jingu.Reactive power optimization of power system based on genetic algorithm and particle swarm optimization algorithm［J］.Journal of Nanjing University of technology 2007，5（29）；58-61

［6］Mashhadi H R， Shanechi H M， Lucas C. A New Genetic Algorithmwith Lamarckian Individual Learning for Generation Scheduling［J］.IEEE Trans. on Power System，2003，8（3）: 1181-1186

［7］周明，孙树栋.遗传算法及应用［M］.北京：国防工业出版社，1999

［8］孙盐丰.基于遗传算法的约束话方法评选［J］.北京交通大学学报，2008， 24（6）:14-19

Modulation Recognition of Diginal's Feature based Improved Genertic Lgorithm

Wang Meng， Cai Minghui
（State Radio Monitoring Center Urumqi Station， Urumqi， 830054）

To estimate the characteristics of modulation identification and modulation parameters values is an important research direction in the feld of signal processing. Based on the improved genetic algorithm，the chapter frst determine the characteristics value assemble of the best performance of signal modulation diffenenrce，take it as the best gene pool，In the genetic process，the steps of selection，cross and elimination cause size change ofexcellent gene pool， cross， eliminated caused by the elite gene pools in the evolution of genetic， in the genetic process，adapt ing the strategy of competition and punishment to optimize the gene pool and ensure each generation are of high quality gene.

genetic algorithm； modulation recognition； feature value extraction； Punish competition

10.3969/j.issn.1672-7274.2015.02.012

TN92文献标示码：A

11672-7274（2015）02-0065-04

王孟，男，1982年生，硕士研究生，助理工程师，现任职于国家无线电监测中心乌鲁木齐监测站。

蔡明辉，男，1985年生，硕士研究生，助理工程师，现任职于国家无线电监测中心乌鲁木齐监测站。