轮毂电机驱动车辆转向节受力计算方法

陈盼，王姝（长安大学，陕西 西安 710064）

轮毂电机驱动车辆转向节受力计算方法

陈盼，王姝
（长安大学，陕西 西安 710064）

论文根据空间力系平衡原理，以转向节为研究对象，建立了轮毂电机驱动电动车转向节受力计算方法。此计算方法分析了在轮毂电机驱动力Mt作用下，麦弗逊悬架系统的受力情况，建立了空间力平衡方程。此计算方法可以根据悬架系统的结构参数、减振器的尺寸与性能参数和整车参数使用MATLAB快速求出轮毂电机作用在转向节上的反向力矩对转向节受力的影响，方便设计人员调整相关设计参数，确定最优方案。

转向节；轮毂电机；麦弗逊；侧向力

10.16638/j.cnki.1671-7988.2015.12.018

CLC NO.: U461.1Document Code: AArticle ID: 1671-7988(2015)12-49-04

引言

电动汽车相比传统汽车主要的不同在于动力驱动系统，电动汽车轮毂电机驱动技术将汽车的动力装置、传动装置和制动装置都整体布置到轮毂内，得以将电动车辆的动力总成机械部分大为简化，使得轮毂电机驱动方式成为最能充分发挥电动汽车电机驱动的优势技术0。

常见乘用车的前悬架系统多使用结构简单，性能可靠，节省空间的麦弗逊悬架。轮毂驱动技术应用于麦弗逊悬架将会是轮毂电机驱动电动车驱动方式的主流方向。文献0已经研究提出了改进的适合轮毂电机驱动的麦弗逊悬架。

轮毂电机驱动的电动车的动力系统从簧载质量转移到轮边，传统汽车的驱动扭矩的反作用扭矩也从车身转移到转向节，受力如简图 1。由图可以看出，轮毂电机驱动的电动车轮边驱动扭矩Mt的反作用扭矩Mt’是作用在转向节上的。此反作用力使得轮毂电机驱动的麦弗逊悬架转向节受力情况不同于传统的转向节。

图1　不同驱动形式车辆转向节上的作用力比较

麦弗逊悬架系统受力计算常见的方法是将悬架簧下质量部分看作整体，通过平面力系平衡关系求解得到减振器侧向力0-0。此方法无法计算轮毂电机驱动情况下，作用在转向节上的电机的反作用扭矩对转向节受力情况的影响，因此不能满足要求。

根据空间力与力矩系的平衡关系，建立了轮毂电机反作用扭矩下麦弗逊悬架系统转向节受力计算模型，提出了不同的驱动扭矩下减振器侧向力计算与分析方法和各个相关悬架结构参数对转向节受力的影响，为以轮毂电机为动力系统的车辆悬架系统设计优化提供了方法。

1、计算模型

1.1模型假设

麦弗逊悬架系统和车身连接部分为具有不同刚度的衬套，为简化计算，现将其连接点简化为铰链连接，下A臂和转向节之间简化成球铰连接，转向拉杆和转向节的链接方式简化成球铰连接；悬架摆臂，转向拉杆，减振器弹簧总成的质量相对较小计算中忽略不计。

1.2建立模型

以轮毂轴承中心平面与前轴轴线交点为坐标原点建立如图所示的局部坐标系；麦弗逊悬架的受力示意图如图2：

图2　麦弗逊悬架系统受力示意图

根据刚体上力的平移定理可以将垂直支撑力N和转向节重力mg移动到轮胎中心作用点，同时附加两个力偶mg·δY和N·δy如图3所示：

“我永远爱她。一个长期单身的男人，对婚姻谈不上什么真知灼见，好比一个体操运动员，在长期中断训练之后，技艺生疏，已无胆量重返赛场。我忘不了她。她带走了我的爱，我连爱的能力都丧失了。”

图3　轮毂中心处受力的局部示意图

以转向节为研究对象，根据空间力系平衡方程可得如下方程组：

以减振器活塞杆为研究对象0，沿局部坐标系X’Y’Z’对O点取距，并定义系数可得：

图4　减振器在局部坐标系X'Y'Z'中的受力简图

由于图2中所示的各个力均为空间力（减振器侧向力在局部坐标系 X’Y’Z’中与三个坐标系平行，但是在坐标系 XYZ中为空间力），需先将各个受力在坐标系XYZ中分解为三个分力。分解方法如下：

（2）由于上部侧向力、下部侧向力和阻尼力的作用点均在减振器轴线上，由几何关系可知：

（3）假设有任意空间力F且F在XZ平面中的投影与X轴夹角为α，F在YZ平面上的投影与Y轴夹角为β，F与F 在 XZ平面上的夹角为γ，在模型中定义（α，β，γ）为方向角，如图5所示：

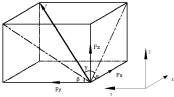
图5　空间任意力的分解

则有如下关系式：

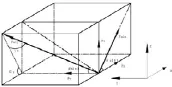
图6　Fulx、Fuly在整车坐标系OXYZ里的方向

（5）工程中常用的减少减振器侧向力的措施为使弹簧的作用线想轮胎一侧偏移距离0，现在假设弹簧力作用线与轮胎轴线的交点到转向主销与轮胎轴线交点之间的距离为 s，减振器阻尼力作用线与轮胎轴线的交点到转向主销与轮胎轴线交点之间的距离为d，如图7所示：

图7　弹簧作用力轴线和减振器轴线示意图

则可以得到如下方程：

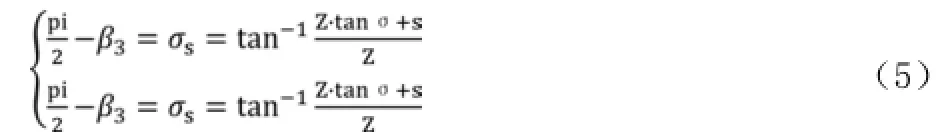
将图2中的所有力按照坐标系XYZ的方向分解后带入方程（1）可得方程（1）的矩阵形式：

矩阵表达式中的Ci（i=1、2、3、4、5、6、7、8、9）表示如下：

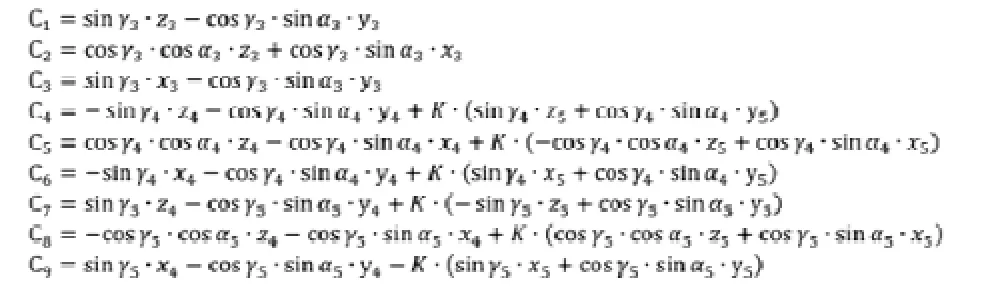
联立求解上述方程组（1）（2）（3）（4）（5）中即可得到。代入方程（2）可求得。至此模型建立完毕。

1.3模型求解

为求得减振器侧向力和轮毂电机反作用扭矩 Mt’的关系并研究对侧向力有影响的其他因素，将某乘用车的前麦弗逊悬挂系统数据输入建立的模型中，求解模型。输入数据如表1所示：

表1　某乘用车前悬架参数

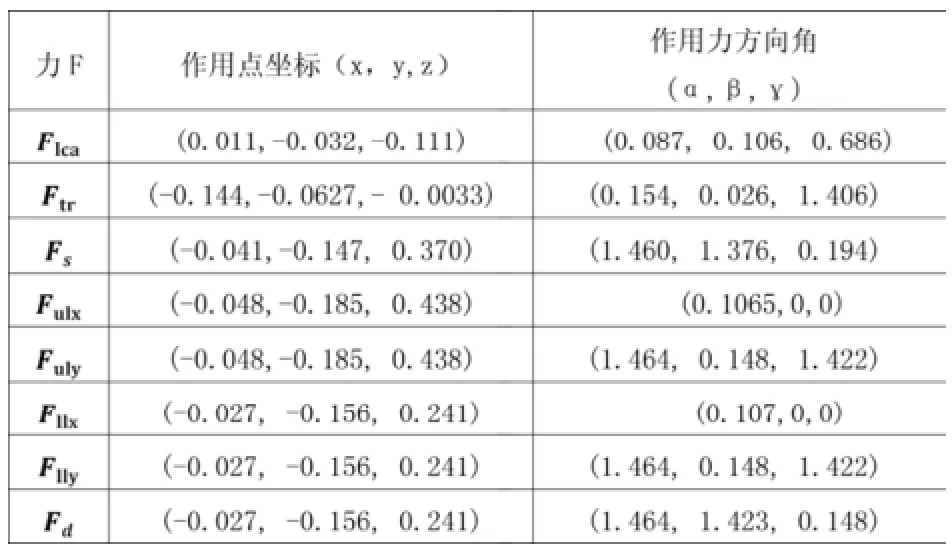
表2　某乘用车前悬架力作用点角度和位置参数

在MATLAB中求解线性方程组（1）即可求解出各个力的数值。减振器套筒和活塞杆之间的侧向力和减振器套筒和活塞之间的侧向力分别为：

设减振器内壁和活塞、活塞杆之间的摩擦系数为μ，那么由于减振器侧向力存在而引起的附加阻尼力为：

2、数据分析

根据上述的计算模型和计算数据可以得到减振器上部侧向力Ful和减振器下部作用力Fll与轮毂电机驱动反作用扭矩的关系，如图8所示：

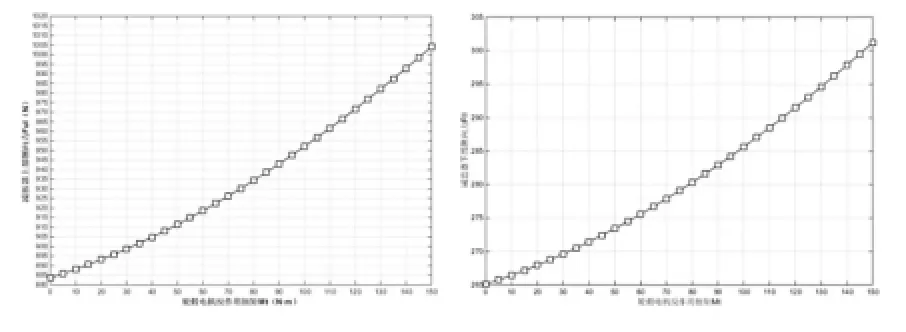
图8　减振器侧向力和轮毂电机驱反作用扭矩的关系

由图8可明显看出，随着轮毂电机驱动扭矩Mt的增大，减振器侧向力Ful和Fll几乎线性增大。

由计算模型可知，代表减振器结构的参数K也会对减振器侧向力产生很大的影响，图9计算了不同的减振器系数下减振器侧向力随着反作用扭矩的变化关系：

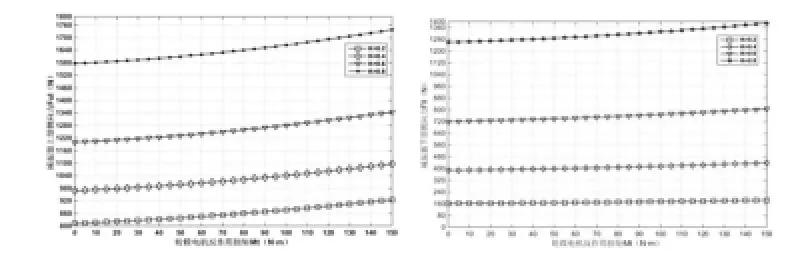
图9　K值变化时减振器上部和下部侧向力随反作用驱动扭矩的变化关系

3、总结

论文根据空间力系平衡原理，以转向节为研究对象，分析了在轮毂电机驱动力Mt作用下，麦弗逊悬架系统的受力情况，建立了空间力平衡方程，可以根据悬架系统的结构参数、减振器的尺寸与性能参数和整车参数快速求出轮毂电机作用在转向节上的反作用力矩对减振器侧向力的影响。根据文中使用的模型计算数据可以得到减振器上部和下部作用的侧向力随着驱动扭矩的变化曲线以及减振器机构参数K对侧向力的影响。这种计算方法可以使设计人员方便地调整相关设计参数，确定最优悬架系统参数方案。

[1] 孟庆华,许进,王东峰.轮毂电机驱动型电动汽车动力系统研究[J].农业机械学报,2013,44(08):33-37.

[2] 陈龙,董红亮,李利明.适合轮毂电机驱动的新型悬架系统设计[J].振动与冲击,2015,34(08):174-180.

[3] 余亮浩,杨德强.基于空间结构的麦弗逊悬架减振器侧向力计算[J].科学技术与工程,2014,14(04):288-289.

[4] 景立新,郭孔辉,卢荡.麦弗逊悬架减震器侧向力优化[J].科学技术与工程,2011,11(01):71-75.

[5] 刘守银,周忍.麦弗逊悬架减振器侧向力分析综述[J].汽车实用技术,2014,(10):44-48.

[6] 周长城.汽车平顺性与悬架系统设计[M].北京:机械工业出版社, 2011:129-131.

A Calculation Method of Suspension KnuckleForce on Hub Motor Driving Car

ChenPan,Wang Shu
( Chang'an University, Shaanxi Xi'an 710064 )

According to the spatial force system balance principle,a new calculation method of Suspension Knuckle Force on hub motor driving car is built which treating knuckle as the research object. This calculation method analyzes the force conditions of McPherson Suspension system under the hub motor drive torque Mt, establishes a spatial force equilibrium equations. The model can be solvedquickly by the software MATLAB according to the structural parameters of the suspension system and vehicle parameters, also can find out the influence of the reaction forceacting on the knuckle, which will cause the lateral force on the damper. The application of this calculation model willgive thevehicle designers more convenience to adjust the related parameters andobtain the optimal solution.

Knuckle; hub motor; Macpherson; lateralforce

U461.1

A

1671-7988（2015）12-49-04

陈盼，就读于长安大学，硕士研究生，研究方向：车辆系统动力学。