客车动力总成悬置系统减振特性与优化研究

许 菁（武汉城市职业学院，湖北 武汉 430064）

客车动力总成悬置系统减振特性与优化研究

许 菁
（武汉城市职业学院，湖北 武汉 430064）

文章通过测量混合动力公交车动力总成的模型参数，在ADAMS软件中建立6自由度悬置系统振动模型，并对模型进行频域的仿真分析，得到悬置系统的固有特性及减振特性，并从系统固有频率配置及振动解耦角度分析该悬置系统的振动特性。由于受整车布置的影响，本文以悬置的刚度参数和发动机前悬置的安装角度为设计变量，以能量解耦为优化目标进行优化设计。

动力总成悬置系统；ADAMS；能量解耦；优化

10.16638/j.cnki.1671-7988.2015.12.012

CLC NO.: U461.4Document Code: AArticle ID: 1671-7988(2015)12-30-03

前言

随着社会的进步和技术的发展，人们对汽车乘坐舒适性的要求不断提高，振动噪声水平已成为衡量汽车性能好坏的重要标准。汽车动力总成悬置系统是汽车振动系统的一个重要子系统，对改善汽车平顺性和降低汽车噪声有很大影响，合理的汽车动力总成悬置系统的设计可以明显降低汽车动力总成和车体的振动。

1、建立动力总成悬置系统模型及其仿真性能分析

1.1动力总成系统模型的建立

本文根据试验车辆配置的动力总成悬置系统，利用ADAMS/View模块对动力总成悬置系统进行三维模型的建立，并将动力总成系统进行简化，忽略了其原有的一部分零部件，本文研究的动力总成是由6个橡胶悬置元件与车架相连的，将6个橡胶悬置由ADAMS/View中的Bushing（轴套）代替。动力总成悬置系统的动力学模型以发动机连接皮带轮的端面与曲轴中心线交点为坐标原点，竖直向上的方向定为Z轴的正向，由齿轮箱到发动机端面定为X轴的方向。

2、动力总成悬置系统频域的仿真

2.1动力总成悬置系统各模态下的固有频率分析

用Adams/Vibration模块中的振动分析，对其静态6阶固有模态进行了计算，结果如表1所示。从表中可知，系统的最高阶模态频率为 24.7333Hz，频域仿真主要针对怠速工况（n=750r/min）、额定工况（2500r/min）和最大扭矩工况（1500r/min）。其振源激励频率和侧倾力矩的大小可由频率计算公式获得，其计算公式为：

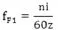
式中，n为发动机转速，r/min；i为发动机缸数；z为冲程系数，2冲程的为1，4冲程的为2。

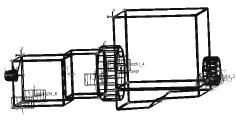
图1　ADAMS中建立的动力总成动力学模型

因此，当发动机怠速工况为n=600r/min时，其激振频率约为30Hz，由隔振理论可知，系统的固有频率应低于激振频率的1/倍，则动力总成悬置系统的最高阶固有频率应低于30Hz的1/倍，即21.213Hz，但6阶固有频率24.7333Hz ＞21.213Hz，因此动力总成系统在转速为n=600r/min的怠速工况下不具有良好的隔振性能。

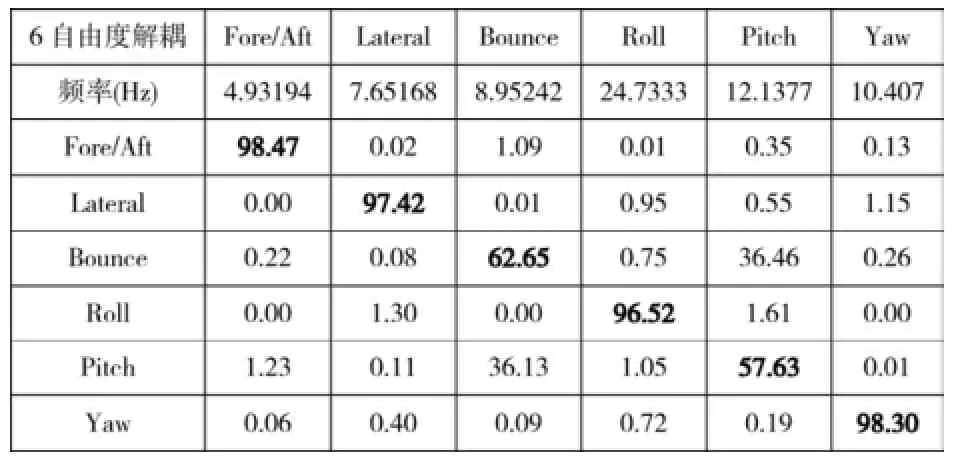
表1　动力总成悬置系统的6阶固有模态及解耦率

表1展示了动力总成悬置系统能量的分布情况，第3阶模态、第5阶模态中沿Z轴平动方向与绕Y轴转动方向极易发生耦合，因此需要对动力总成悬置系统进行解耦设计，希望系统沿Z轴平动方向、绕X轴转动方向的解耦能达到90%以上，但由仿真计算可知，系统沿Z轴平动为主要振型的第3阶解耦率低于80%，极大影响系统的隔振性能，降低车内的舒适性，应对其进行优化设计。

3、动力总成悬置系统的优化

3.1目标函数

本文优化的目标是发动机产生振动的2个主要方向，使垂直方向（坐标系Z轴方向）和绕曲轴方向（X轴方向）的解耦达到较大值（90%以上），并将系统各阶固有频率的取值范围作为约束，对悬置系统进行深入优化。

3.2设计变量

由于受到安装空间的限制，在实际优化过程中往往都是采用原有的悬置布置方案，并不改变悬置元件的支承位置和角度。因此，本文将悬置元件3个主方向的刚度以及发动机左右前悬置的安装角度作为设计变量进行优化设计。悬置元件刚度的优化的变化范围取±60%，悬置安装角度的变化范围为30°～60°。

3.3约束条件

3.3.1悬置系统固有频率的约束条件

悬置系统的最高固有频率上限应为 20Hz，另外垂直方向的固有频率应避开4～8Hz的人体敏感频率范围，综合考虑悬置系统固有频率的下限应为5Hz。

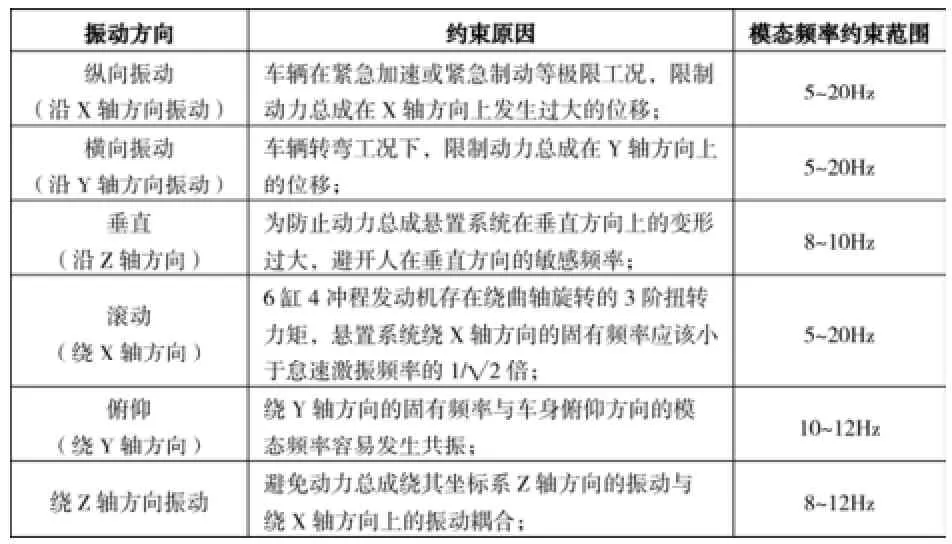
表2　模态频率约束范围

3.3.2动力总成系统沿X轴、Y轴振动位移及转角约束

动力总成悬置系统在实际工作过程中，其质心位移变化不易过大，一般要求动力总成悬置系统质心沿坐标系Y轴方向的位移不超过 1mm，沿 X轴方向的位移不超过 3mm，沿Z轴正方向的位移小于10mm，沿Z轴负方向的位移小于20mm，转角为不大于3°。

4、优化结果分析

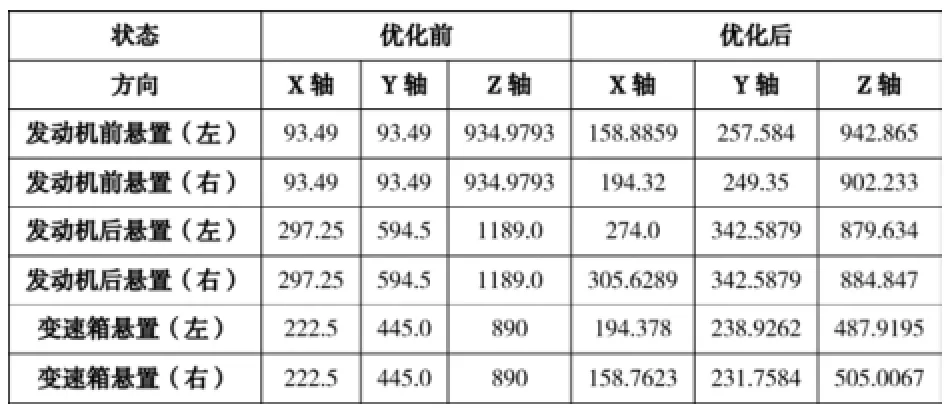
表3　优化后悬置各方向的刚度值（N/mm）

运用设计评价（Design Evaluation）中的优化计算（Optim ization），对悬置系统进行优化。经过多次计算及调整得到优化后的悬置参数：安装角度从原有的 45°变为优化后的30°，6个悬置3个方向的优化前后刚度如表3所示。

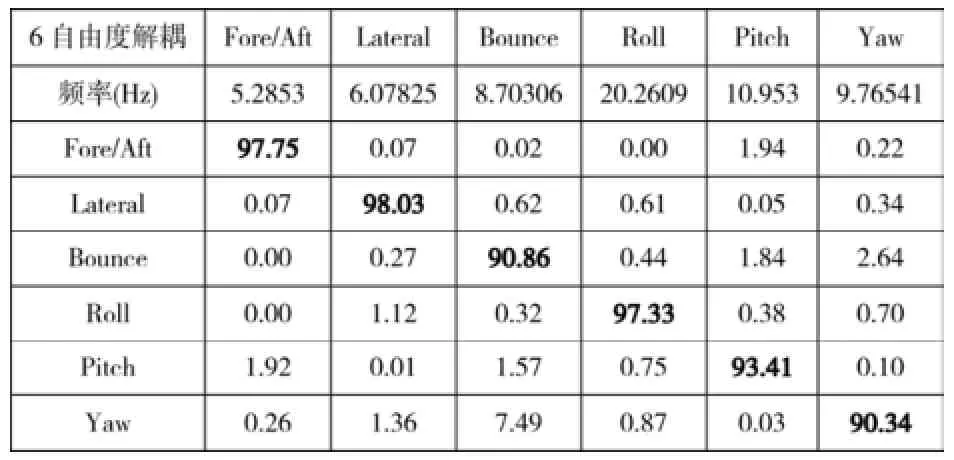
表4　优化后动力总成悬置系统的6阶固有模态及解耦率

优化后的动力总成悬置系统的6阶固有模态及解耦率如表4所示，与优化前的数据相比，优化后的悬置系统最小频率值为5.2853Hz，大于固有频率最低下限5Hz。悬置系统的最高阶固有频率，即绕曲轴方向转动的固有频率从原先的24.7333Hz降低至 20.2609Hz，远离发动机最低怠速工况（n=600r/min）激振频率的1/倍21.213Hz，不易发生共振现象。从整体来看，各阶固有频率之间的最小间隔为0.7Hz，可以避免各阶模态之间发生共振。从悬置系统的各模态的解耦情况来看，优化后的悬置系统在Z轴方向与θy方向的解耦分别达到90.86%和97.33%，与优化前相比分别提高了28.21% 和39.7%；其余几个方向的解耦率均达到了90%，因此整体来看该悬置系统基本实现解耦，达到了解耦优化的目标。

[1] 张永利,王永,苑吉友.合肥工业大学学报(自然科学版) [J].合肥工业大学.2007,15( S1)：45-48.

[2] 庞剑,谌刚,何华.汽车噪声与振动:理论与应用[M]. 北京:北京理工大学出版社,2006，124-126.

[3] 徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程.1992.14(2):103-110.

[4] 温任林.颜景平.汽车发动机悬置系统多目标优化的研究[J]. 东南大学学报.1996，26(6A)105-110.

[5] 季晓刚,章应雄,唐新蓬.汽车动力总成悬置研究的发展[J].汽车科技,2004.1(1):4-6.

[6] Jong-Hyum Ki.Influence of Chassis Flexibility on Dynamic Behavior of Engine Mount System[J].SAE 942269.

Study on the Vibration Attenuation Characteristic and Optimization of Bus Powertrain Mounting System

Xu Jing
( Wuhan city vocational college, Hubei Wuhan 430064 )

The paper according to the test, the hybrid electric bus power-train parameters were test . Then a six degree of freedom model of the mount system is built up by using ADAMS. And based on the model, the vibration attenuation performance of the powertrain mounting system was simulated under the idle speed condition in frequency domain .Vibration characteristics including natural frequencies and decouple rates are analyzed then. Because of the influence of the whole vehicle arrangement, this paper takes the stiffness parameters of the mount components and the installed angle of engine front mounting were optimized design variables，takes the energy decoupling of the powertrain mounting system as the optimizing goal.

powertrain mounting system; ADAMS; energy decoupling; optimization

U461.4

A

1671-7988（2015）12-30-03

许菁，就职于武汉城市职业学院。