超深井井下环境仿真系统温度场数值模拟
艾 岭,朱 奕,伞 冶
(1.哈尔滨工业大学 控制与仿真中心,150001哈尔滨;2.哈尔滨理工大学 自动化学院,150080哈尔滨)
随着石油钻探技术的发展,油田深井井下环境日益复杂,深度超过7 km,油层温度和压力已达到300℃及200 MPa以上[1],这就使各种新型射孔器材的研制速度不断加快,对各厂家新产品的检测和质量标定的要求也迅速提高.目前,随着射孔器材检测标准的日益完善,对相关检测理论的深入研究以及新型检测设备的研制已迫在眉睫.其中,射孔器材的耐温耐压性能是检测射孔器材质量的重要指标.新型射孔枪的最大外径达到178 mm,检测长度达到2~5 m.油田超深井井下环境仿真系统(以下简称“仿真系统”)就是在地面模拟深井井下的高温超高压环境,对射孔器耐温耐压性能进行检测的一种高精度实验设备[2].
由于实际测量位置有限,无法完全体现系统的分布参数特性,作为系统检测的重要指标,获得准确的釜内温度场分布是系统设计成功的关键.作为一类特殊的高精度大型检测设备,国内外对此类仿真系统温度场建模和控制的相关报道非常有限[3].目前,由于环境仿真系统温度场同时具有大滞后、大惯性和分布参数特性,尚无可直接借鉴的分析方法.在已取得的成果中,已得到对系统传热特性的初步认识[4-6].但是,由于早期受研究条件的限制,无法通过理论分析和实验研究等方式直观获得整个系统温度场的温度分布情况.随着计算机技术的发展,流体数值仿真技术发展迅速[7],特别在近几年.然而,针对封闭方腔的研究,多集中在一致长径比和气体填充介质[8-9],尚没有针对类似于本仿真系统的多层介质及釜内为热传导液的研究.
本文利用流体仿真方法,数值模拟了仿真系统温度场和流场的分布情况.首先,介绍了仿真系统的组成和工作原理;然后,利用传热学基本理论,建立了系统不同传热介质的热传递模型;最后,建立系统的结构化网格,并按不同炉温升温曲线进行流场和温度场数值仿真,得到系统的速度场和温度场的分布情况,并与实际升温曲线进行对比,为解决仿真系统的温度场控制问题提供了理论依据.
1 仿真系统组成
井下环境仿真系统包括高温超高压釜体、加热系统、超高压液压系统、电气系统、计算机控制系统等,工作原理如图1所示.其中,高温超高压釜为系统的工作主体,内外径比为0.517,长径比为20,整体材料由特种钢组成,包括釜体和上下两个塞体,倾斜20°角俯卧在井式电加热炉上,内部可同时放置若干支长度6 m以内的射孔枪进行耐温耐压实验;加热系统由井式加热炉、循环风机和调整各区加热功率的电气系统组成;超高压液压系统由超高压泵、控制阀和液压管路等组成,炉体结构如图2所示;计算机控制系统包括工业控制计算机、Compactlogix系统和智能温控仪表组成,实现对加热系统和液压系统的远程控制,温度压力算法的实时监测和控制功能.

图1 控制系统结构

图2 炉体结构
系统的工作过程可分为井口作业、供油循环、升温升压、保温保压和泄压冷却等5个步骤:
1)井口作业.将待检测的射孔枪喷砂处理后放入高压釜内并拧紧釜盖;
2)供油循环.利用液压系统,热传导液通过供油泵、单向阀、4号控制阀进入釜内,充满釜内空间;
3)升温升压.系统采用先升温再升压的工作方式,启动风机选择内循环风模式,通过智能温控仪表调整可控硅的导通角调整各区加热器功率达到对釜体均匀加热的目的,在温度达到设定值后,启动供油泵和超高压泵,热传导液通过3号控制阀进入釜内,使釜内压力升高;
4)保温保压.在压力和温度达到设定值后,保持温度、压力一段时间,检验被测射孔器材的耐温耐压性能;
5)泄压冷却.在达到保温保压时间后(或由于射孔器无法承受压力和温度使实验中止),依次打开1号和3号控制阀进行泄压,同时关闭加热器,选择外循环风模式冷却釜体,待温度降到安全值后,将试件取出,实验结束.
按工艺要求,系统的工作流程如图3所示.系统具有多层导热介质,存在多种热传导形式,包括井式电加热炉与釜体外壁、电加热元件、保温层的对流-辐射换热,釜体自身热传导,釜体内壁与热传导液、热传导液与射孔器的自然对流,而由于井式电加热炉为一低温电阻炉,保温层热阻很大,热损失较小,射孔器内部为中空结构,对周围温度场影响也可以忽略,系统剖面如图4所示.由于传感器数量有限,无法完全体现系统的分布参数特性,所以有必要分析系统的传热机理,特别是对釜内热传导液对流传热机理进行分析.
2 传热学模型
从理论上研究井下环境仿真系统的传热过程,包括对釜内热传导液自然对流、釜体热传导以及炉膛空气强迫对流的传热过程.

图3 系统工作流程
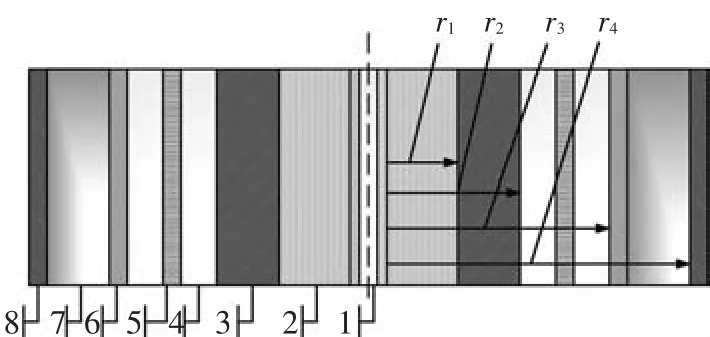
图4 系统剖面示意
2.1 热传导液自然对流
自然对流是由于流体内部温度变化导致密度变化引起的,因此产生的传热过程称为对流换热[10].釜内热传导液的自然对流可以看作是一个由釜体内壁与热传导液温度差引起的三维封闭空间的流动.在连续介质假设下,热传导液流动应满足连续性方程、动量方程、能量方程[11]:
1)连续性方程

2)动量方程


3)能量方程,无内热源、忽略耗散函数时对流换热能量方程为
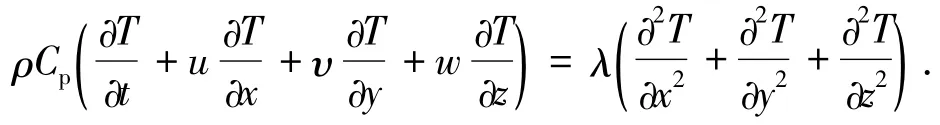
热传导液的流动强度由瑞利数(Ra)决定:
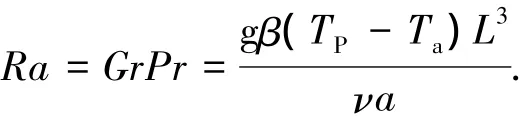
其中:Cp为比热容;β为膨胀系数;取L=6;ΔT≤100;g为重力加速度;热传导液瑞利数Ra的数量级为1010~1013.一般认为,当Ra超过109时,湍流开始发生.由于湍流微团的尺寸相比分子的平均自由程大得多,及分子间无规则碰撞频率要高于湍流的速度脉动,所以,连续方程和Navier-Stokes方程对湍流仍能够精确描述,不过此时想获得方程的正确解却比较困难.
2.2 釜体传热模型
根据所研究的对象具有轴对称的特点,选择柱坐标系描述方程,内外釜壁、隔热材料内部的导热方程可表示为[9]

仅考虑径向的传热过程,方程可简化为一维线性偏微分方程:

其中热扩散系数a=k/(ρ·Cp).假设井式加热炉分为上下两个区,左边界温度由炉温控制,右边界与釜内热传导液形成自然对流换热,可在釜壁外等间距安装温度传感器测量釜壁温度:
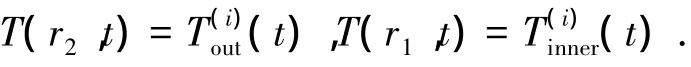
其中:T(·,t)表示温度;r1、r2分别表示釜体内外半径;i=1,2表示两个循环区.由于系统一般均在稳态时开始加热,加热初始时釜体温度场均匀,得到方程的初始条件为

釜体本身可近似为内半径r1=0.3 m、外半径r2=0.58 m的中空柱体,釜内有效长度L2=6 m,上下塞体长L1=0.7 m.如图5所示,内部充满热传导液,釜体材料为镍铬特种钢.

图5 釜体截面
2.3 加热炉温度模型
井式电加热炉是系统能量转化和传递的起点,高温热电阻通过对流加热炉膛空气,同时通过辐射对釜体表面传递能量,仅利用能量方程给出炉膛传热模型的基本方程.空气与两壁面对流换热的热平衡:
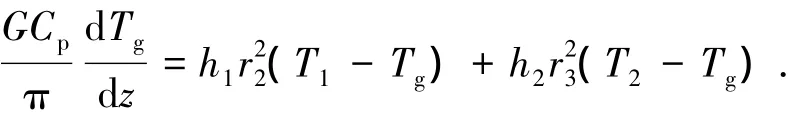
釜表面的热平衡:
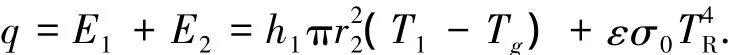
其中:G为炉膛内空气流速;Cp为比热容;Tg、T1、T2、TR分别为空气、釜外壁、保温层、电热丝的温度;h1、h2分别为釜壁、保温层对流系数,r2、r3分别为釜体外径、炉壁内径,q为釜表面吸收热量,ε为黑度;斯波兹曼常数σ0=5.67×10-8W/(m2·K4).当炉膛内空气强迫对流时,对流换热E1占主导地位,当自然对流时,辐射能E2占主导地位.
3 数值模拟
仿真系统各部分材料在常温下的热物性如表1所示;计算过程中由于釜体、空气、炉壁的热物性参数变化较小,可以按常物性进行求解,由于温度变化过程中,热传导液的热物性参数变化较大,其在不同温度下的热物性参数如表2所示.

表1 材料在常温下的热物性

表2 不同温度下热传导液的热物性
由于系统是一个立体的三维结构,釜内热传导液的自然对流属于三维流动,对三维方程的数值求解十分复杂,由于釜体是轴向对称的,在忽略端部效应后,可以将系统传热问题简化为一个二维厚壁密闭方腔的导热对流问题.设釜体内径为0.3 m,外径0.58 m,长度6 m,釜体倾斜20°俯卧在井式电加热炉上,釜体两端各有0.2 m处于炉体外;釜体内壁有一根直径4 mm的高压管紧贴釜体内壁,其长度接近上塞体,为避免与边界层混叠产生较大误差,将此出口设置于上塞体的中间位置;根据自然对流边界层理论,由于热传导液的Pr数很大(大于100),热边界层厚度很薄(仅有几个mm),必须对釜体内壁面边界层网格进行加细,网格划分应用ANSYS ICEM设计,采用具有较高收敛能力的四面体结构网格.
选择Ansys Fluent软件进行流体数值模拟.为研究方便,设出口压力为1个标准大气压,初始温度为20℃,除釜体外壁与炉体接触部分外,其他边界绝热.仿真模型采用重整化群(RNG)k-ε湍流模型,釜体内壁采用标准壁面函数;离散算法采用SIMPLE算法,应用PRESTO!压力修正方法,动量方程离散格式为二阶迎风格式,能量方程和耗散方程离散格式为一阶迎风格式.
设釜体外壁空气强迫对流传热均匀,平均对流系数为200 W/(m·s),被平均分为上下两个循环区域,每个区域的流场温度均匀,根据低温炉及加热工作特点,忽略辐射效应;将目标温度设为150℃,边界条件设置为对流边界条件,由于加热元件功率和釜体吸热放热等物理条件限制,并避免釜体受到热冲击变形引起釜体使用寿命下降等因素,炉温变化速度不能过快.
在对釜体外壁进行均匀加热的情况下,将热传导液温度场视为集中参数系统,为了得到最终温度目标值,采用多次调整的方法,找到系统的最优升温曲线,如图6所示.图7、8分别给出了系统在t=2、3、4 h时的温度场分布和速度场分布.

图6 炉温升温曲线
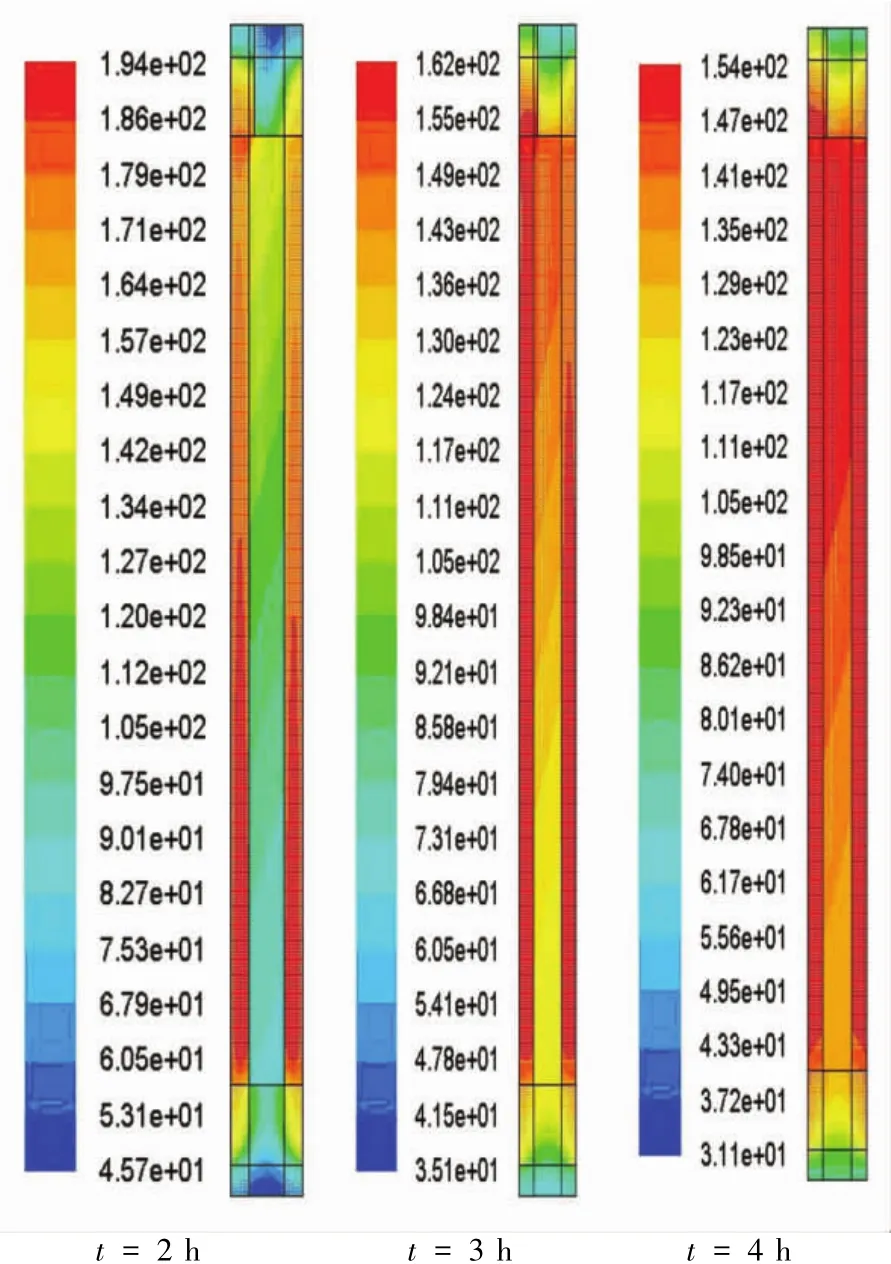
图7 炉温均匀时系统温度场

图8 炉温均匀时热传导液速度场
从理论上分析图9和图10.由炉膛均匀地加热釜体,釜体受热后,又对热传导液进行加热.在加热过程中,由于对流作用,紧贴釜体内壁的热传导液受热膨胀,密度下降,产生浮升力使自身上升产生对流,同时将热量传递给内层热传导液.由于釜体密闭使中间热传导液向下流动,层流流动逐渐发展为湍流流动,同时传热效率逐渐增加,釜内热传导液温度呈现上高下低的温度分层现象,温差逐渐扩大,等温线基本同重力方向垂直,热传导液在釜体顶部和底部较活跃,基本同釜内温差较大的位置保持一致.为了更好地分析系统传热特性,图9、10分别给出了釜内轴向(射孔器放置位置)温升曲线、中轴线自下而上在x=[0.1 1.5 2.5 3.5 4.5 5.9]6个位置上的温升曲线.

图9 炉温均匀时热传导液温度场
由于釜壁和热传导液具有很大惯性,釜内热传导液升温会有约30 min的延时;另外,在均匀炉温和均匀对流传热系数条件下,釜内热传导液轴向的升温速度和稳态温度会存在一定的差别,釜顶达到设定温度时自上而下的温差约为20℃,而继续加热,釜底温度继续上升,但升温速度很慢.

图10 炉温均匀时热传导液升温曲线
为了验证数值模拟结果的有效性,采用一致炉温对实际系统进行升温试验,实测温度曲线如图11所示.可以看到,由于热传导液循环使釜顶初始温度稍低,在1 h后热传导液温度开始快速上升,升温速度釜体上部明显快于下部,在3 h后升温速度开始减慢,两者在平衡状态时温差约为18℃;稳态时实测升温过程和数值模拟结果偏差≤2℃.从图9~11可以看出,可以用自然对流基本理论解释系统的传热过程,仿真结果与实测结果基本一致.

图11 实测升温曲线
从理论分析和实际结果可以看出,均匀加热导致热传导液产生温度差的原因是由于热传导液在惯性力作用下引起的.为了使轴向温度均匀,必须通过改变釜内自然对流形态来改变釜内温度场分布,一个有效的办法是使釜体上下产生一定温差,此时,热的热传导液由于在釜体上部不能持续加速而提前转捩,从而使釜内产生湍流.设定加热炉1区炉温为400℃,加热炉2区延时升高且炉温设定为210℃,从而实现对热传导液的分区加热,使釜体内壁轴向初始阶段就产生一定温差,炉温升温曲线见图12,最后调整温度差和加热时间,得到系统温度场和速度场分别见图13、14.
对比图13、14炉温可知,前者轴向升温均匀,整体加热时间段(炉温为400℃)短,而后者整体加热时间长,热量主要从第I加热区对釜体加热,II区对釜内热传导液传热相对较少;从图13可以看到,釜壁温度变化与炉温变化规律一致,釜体温度明显分为上低下高两个区域,升温速率和升温时间都有不同,外壁温差最大接近70℃,内壁温差最大可达40℃,底部的端部效应比较明显,最终釜体温度保持在设定温度不再变化;观察图14可以看到,釜内热传导液也产生湍流并形成环流,从而使温度场温差缩小.
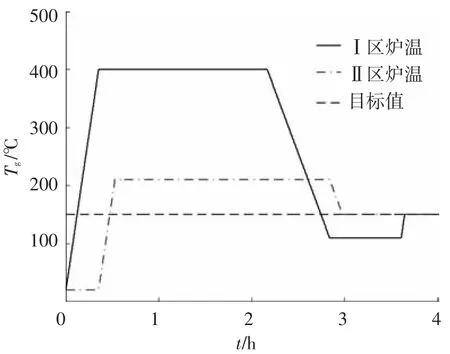
图12 炉温升温曲线

图13 无温差时系统温度场

图14 无温差时热传导液速度场
从图15、16可以看到,热传导液升温速率均匀,在反复调整升温曲线后,加热3.5 h后热传导液温度可均匀地达到设定温度值,并能够保持在设定温度上.
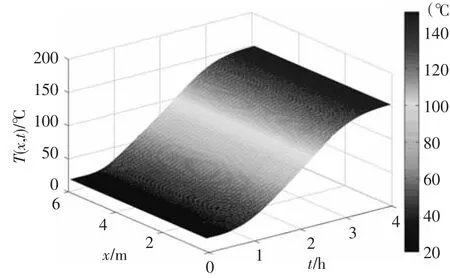
图15 无温差时热传导液温度场

图16 无温差时升温曲线
根据系统温度场分布特点,可以将系统简化为具有时滞的轴向分布的一维系统,在系统工作区内进行多次仿真,得到系统的训练数据,再通过分布参数系统建模方法建立系统的温度场数学模型[12],改进已有的控制算法,得到釜内温度控制的闭环控制算法,达到对系统温度场的精确控制要求[13-14].
4 结 论
1)从数值模拟和实验结果可知,系统传热过程具有明显的分布参数特性,在釜体长径比较大的情况下,将热传导液传热过程按集中参数模型进行处理,会使热传导液轴向产生较大温度差.为保证釜内温度场轴向温度均匀,必须根据分布参数系统方法设计控制器.
2)分区设置炉温,使釜体内壁温度上下产生一定温度差,可以实现釜内温度场的均匀分布,但温差过大会引起釜体下部温度比上部偏高,且影响整体升温时间,灵活设置温差可在系统有限功率下既保证釜内环境温度均匀,又能有效提高升温速率.
3)按所提方法调整炉温升温曲线,实现了对釜内温度场的开环控制,满足了系统稳态温度场性能要求.
[1]王海东,孙新波.国内外射孔技术发展综述[J].爆破器材,2006,35(3):33-36.
[2]伞冶,刘俊强,刘翠玲,等.油田深井井下环境仿真系统设计[J].系统仿真学报,2001,13(1):43-46.
[3]刘翠玲.油田超深井环境仿真系统研究[D].哈尔滨:哈尔滨工业大学,2002.
[4]刘翠玲,王子才.油田超深井环境仿真系统的一体化模型研究[J].计算机仿真,2006,23(3):193-196.
[5]刘翠玲,王子才,陈建明,等.高温超高压釜加热过程的预测模型与研究[J].哈尔滨工业大学学报,2001,33(5):697-699,705.
[6]陈建明,王子才.射孔器耐高温超高压检测系统控制方案与实现[J].哈尔滨工业大学学报,2003,35(3):311-314.
[7]HE Y L,TAO W Q,ZHAO T S,et al.Steady natural convection in a tilted long cylindrical envelope with lateral adiabatic surface Part 1 Theoretical modeling and numerical treatments[J].Numerical Heat Transfer,2003,44:375-397.
[8]SHEREMET M A.Three-dimensional conjugate natural convection in a vertical cylinder under heat transfer to the surroundings[J].Fluid Dynamics,46(4),2011:647-657.
[9]KURIAN V.Numerical studies on laminar natural convection inside inclined cylinders of unity aspectratio[J].International Journal of Heat and Mass Transfer,2009,52(3):822-838.
[10]李友荣.高等传热学[M].北京:科学出版社,2013.
[11]KAYS W M,CRAWFORD M E,WEIGAND B.对流传热与传质[M]第4版.赵镇南,译.北京:高等教育出版社,2007.
[12]LI H X,QI C K.Modeling of distributed parameter systems for applications A synthesized review from timespace separation[J].Journal of Process Control,2010,20(8):891-901.
[13]李健,刘允刚.一类不确定热方程的自适应边界控制[J].自动化学报,2012,38(3):469-473.
[14]AI L,SAN Y.Model predictive control for nonlinear distributed parameter systems based on LS-SVM[J].Asian Journal of Control,2013,15(5):1407-1416.

