基于“搜索+优化”的主动解列断面选择方法
王乙斐,刘涤尘,廖清芬
(武汉大学 电气工程学院,湖北 武汉 430072)
0 引言
随着我国互联电网规模不断地扩大,系统中某区域的局部扰动将通过联络线快速扩散至整个电网,严重者会引发大停电事故[1-4]。失步解列作为保证大电网安全稳定运行的第三道防线,是防止电网大面积停电的重要手段[5-8]。
在多数情况下,电网实施被动解列后,系统内部容易出现发电机出力与负荷之间的极不平衡功率,电网仍需要采取切机、切负荷等措施才能使系统达到稳定[9-11]。而主动解列则根据系统的在线运行水平与故障信息,对故障严重性进行准确评估,在短时间内找到使孤立子系统迅速恢复稳定的最优断面,主动将整个网络分解为若干个孤岛,有效减少了切机、切负荷等操作,保障了电力系统安全稳定地运行[12-14]。因此,主动解列是未来解列控制系统发展的新方向。
解列点选择是主动解列决策过程中的where问题,目前也是研究的热点[5]。从理论角度分析,系统中每一条线路皆是潜在的解列线路,解列时需要对网络中所有线路进行搜索。这样,原始解列策略数量将随着网络规模扩大呈几何级数增长,难以满足计算快速性要求[15-16]。如果能在不影响最终解列断面的前提下降低网络维数,消除冗余信息,在缩小后的求解空间中搜索解列断面,将对主动解列具有重要意义。
文献[10]基于调度分区的方法,从失稳区内边界子区域的外层节点与剩余区间的联络线中搜索解列断面,满足在线应用的快速性要求,但未将子系统内部发生失稳的情况考虑到可控范围内。文献[15]提出基于决策空间预筛的解列策略搜索算法,该方法能够在不损失可行解的前提下极大地减小决策空间规模,但较难进行节点辨识。文献[16]依据慢模式特征值大小对线路进行直接处理,有效避免了整个网络节点的划分,但该方法计算冗长,且运行方式的变化会影响最终判断结果。文献[17]利用有向二元决策图(OBDD)法将解列断面的求解问题转化为带约束边割问题,有效减小了系统决策空间,但该算法的复杂度成幂级数增长,当系统增大到一定规模后,受计算机内存影响,策略搜索将无法继续完成。
本文在现有相关研究的基础上,提出了一种新解列断面选择方法。该方法无需对系统弱连接进行识别,也没有失稳模式的限制,可迅速缩小求解空间确定解列断面,并能对最终解列面作优化处理,为主动解列控制的实现奠定了基础。基于CEPRI 36节点系统和IEEE 118节点系统的仿真结果验证了该方法的有效性与正确性。
1 “搜索+优化”的理论特性
如图1所示,失稳后系统中的节点由两部分构成:一部分是单独与某机群(如Area1或Area2)存在强耦合联系的节点,以空心圆圈表示;另一部分是与几个机群(如Area1和Area2)共同存在强耦合联系的节点,以实心圆圈表示。而大量实践经验表明,系统最终的解列断面实质上是在共同拥有的区域中寻找使解列后子系统平衡的点的集合。因此,若能将系统中某机群单独拥有的节点(如空心圆圈所示)消除,则可排除大量非可行解列策略,加快系统的搜索速度。
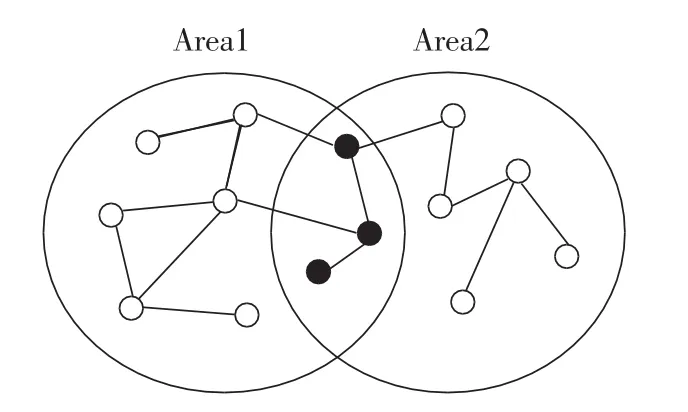
图1 系统失稳后网络结构Fig.1 Network structure of instable grid
由图1可知,降维后系统的求解策略空间由2a降低至2a-b,其中a为原始节点数,a-b为公共区域中节点数。若能将断面搜索问题从整体深化到局部,在2a-b维空间中进行断面搜索,并以功率平衡为原则加以调整,则能确定最终断面。因此,本文提出了一种“搜索+优化”的综合算法,该算法分3步进行,其中前2步属于“搜索”,第3步属于“优化”。首先应用Floyd算法对采集到的潮流信息进行分析,得到系统内各节点之间的最短电抗累积和,保留与失稳机群均存在强耦合联系的公共区域,完成对网络结构的降维处理;然后根据失稳时各节点电压相角的暂稳特性,对第1步得到的公共区域做二次处理,将其包含的节点划分到相应的集合中,则可确定初始解列断面;最后以解列原则对初始解列面进行调整优化,得到满足孤岛功率平衡约束的解列面。具体流程图如图2所示。
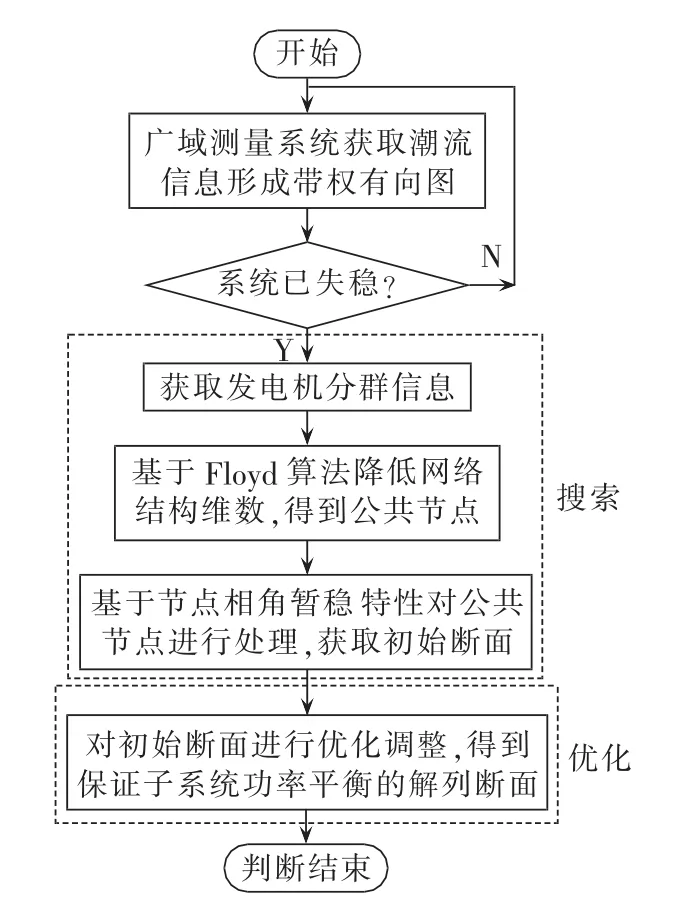
图2 “搜索+优化”实施过程Fig.2 Flowchart of “searching+optimization”
2 基于Floyd算法化简网络结构
Floyd算法是一种解决最短路径规划的算法,目前已广泛地运用在网络通信领域、交通运输、信息包传递等方面。电力网络也是典型复杂网络中的一种[18-20]。 因此,本节将利用Floyd算法求解节点之间的最短电抗累积和以化简网络结构。
2.1 最短电气距离的数学特性
电力系统的拓扑结构可描述为由顶点和边组成的带权无向图G(V,E),其中V为电网中所有发电机、变电站和负荷节点的集合,V={v1,v2,…,vp};E 为一组有权边的集合,E={e1,e2,…,eq}。 系统中任意一条弧为lij=(vi,vj),为与解列操作的实际应用相结合,本文用节点vi与节点vj间边的电抗值xij表示lij上的权值。边权值反映了相邻节点间耦合的强弱程度。
假设系统G中,顶点vr到顶点vs存在h条路径,t为h条路径中任意一条,定义路径t的权Wt为t中所有弧的权值之和,即:

其中,xij∈t表示xij为构成路径t的线路元素。
若h条路径中的某一条路径j的权值满足Wj=min{Wt,t∈h}(j∈h)(t∈h、j∈h 分别表示路径 t、j为 h条路径中任意一条),则称Wm为顶点vr到顶点vs路径的最短电抗累积和。
两点间最短电抗累积和的大小在一定程度上反映了网络中节点间电气联系的强弱[18-20]。其值越大,说明两点之间距离越远,电气耦合程度越弱;其值越小,说明两点之间距离越近,电气耦合程度越强。因此,两点之间最短电抗累积和路径实质上表征了两点之间联系最强的路径。
2.2 Floyd最短路径算法
Floyd算法的核心思想是在未标记的点中选择一个权值最小的弧段[21-23],进行循环比较的过程。本文将该算法运用于求解节点间最短电抗累积和,主要分为以下几个步骤进行。
a.获取系统的暂态稳定性,判断机组分群情况,假设系统受大扰动失去稳定后分为m个机群。
b.假设系统 G=(V,E)中共包含 n个节点,y个发电机节点vG,用集合VG表示;u个负荷节点vL,用集合 VL表示;y+u=n,VG∩VL= ,V=VG∪VL。 首先,构造系统的带权邻接矩阵W。

c.在MATLAB中编写Floyd算法程序,计算任意两节点间的最短电抗累积和,提取其中发电机与负荷节点间的最短路径部分构成矩阵。
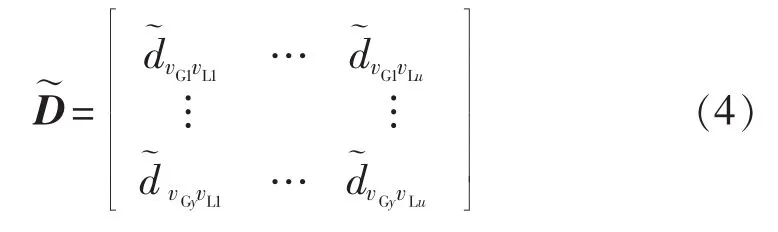
d.已知系统受到扰动后分为m个机群,若要得到系统中负荷节点到不同同调机群的最短电抗累积和,则通过计算到该同调机群中所有机组的最短电抗累积和的平均值来确定。
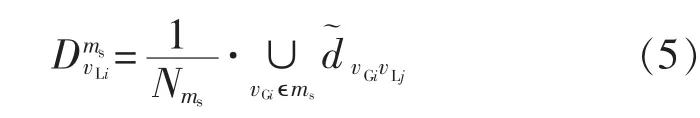
其中,ms为某一机群;Nms为机群ms所包含的发电机数量;为负荷节点vLi到机群ms的最短距离。
2.3 节点辨识
假设ma、mb为m个机群中任意2个机群,节点vLi到这2个机群的最短平均距离之差,大小的实质表征了节点vi与这2个机群电气强弱的比较。设定ε为阈值,若,表示负荷节点vLi与2个机群的联系相差较大,节点vLi与某一个机群存在强联系,定义这种节点为一般节点(如图2中空心节点所示),主导机群可由μ的正负确定;若,表示负荷节点vLi与机群ma、mb之间联系的强弱程度接近,将该种节点定义为公共节点vp(如图2中实心节点所示)。其中,ε的整定可根据实际电网的特性分析、统计数据、运行经验进行具体整定。如果阈值取值过大,会导致公共节点数目过多,增加第2阶段计算的复杂度;阈值取值过小,会导致第2步搜索空间过小,丢失可行解。因此,本文通过对CEPRI 36节点和IEEE 118节点系统进行故障扫描,选择0.05作为阈值门限。
如第1节中所述,将系统中的一般节点消除,对公共节点所在区域进行重点研究,能够在较小的范围内寻找系统的解列策略,从而减小搜索问题的求解规模。
3 基于暂态特性的节点划分
由第2.2节可知,G是一个nG机系统。假设系统受扰后 nA台发电机相对于 nB台机组失稳[24],nA+nB=nG。nA台发电机组成机群A,nB台发电机组成机群B。发电机节点vGi、vGj与系统中任意非发电机节点即负荷节点vLk,在系统中所处的情况有以下几种。
a.当{vGi,vGj}∈机群 A,其电压相角 θi≈θj,节点vLk处的电压相角 θk如式(6)所示。

b.当{vGi,vGj}∈机群 B,其电压相角 θi≈θj,节点vLk处的电压相角 θk如式(7)所示。

c.当 vGi∈机群 A、vGj∈机群 B 时,电压相角 θi≫θj,节点 vLk处的电压相角 θk如式(8)所示。

基于上述理论分析,可通过将失步机组发电机节点电压相角的平均值与公共节点电压相角θk进行比较,把公共节点分到2个集合Va和Vb中,集合Va包含了失步的nA台发电机及部分负荷节点,集合Vb包含了失步的nB台发电机及其余的负荷节点。具体步骤如下。
a.对系统实际监测预设点处的联络线电气量进行捕捉,获取系统分群情况与节点电压相角。
b.基于系统分群情况,计算失步机群A内发电机节点电压相角平均值计算失步机群B内发电机节点电压相角平均值。做比较。 若
c.将公共节点电压相角 θk与,则说明 vLk∈Va;若,则说明 vLk∈Vb。
d.重复进行步骤c直至所有公共节点分入相应的集合中,完成节点划分。
上述步骤仅针对失步为两机群情况而言,若为多机群时,则可按照相同的方法进行两两比较。因此,采用该方法对公共节点进行处理,能将其划分到相应的集合中,寻找到初步解列断面。
4 算例分析
为验证本文所提方法的有效性与快速性,在电力系统综合分析程序(PSASP)和MATLAB中进行仿真计算。
4.1 CEPRI 36节点系统
CEPRI 36节点系统是中国电科院的标准算例,该系统包括8台发电机、36条母线以及32条交流线,总发电量为2652 MW,总负荷量为2567.8 MW,基准功率为100 MW。
4.1.1 搜索初始解列断面
假设系统0 s时在线路19-30上发生三相接地短路故障,0.2 s后清除故障。发电机群Ⅰ{G7,G8}相对于发电机群Ⅱ{G1,G2,G3,G4,G5,G6}失步。 根据图2所示的简化网络流程图,在已知发电机分群信息之后,采用Floyd算法求解负荷节点到机群Ⅰ、机群Ⅱ的最短电抗累积和之差 μ(μ=DIvLi-DⅡvLi),结果如表1所示。
由表1可知,当ε=0.5时,系统所包含的公共节点为 14、15、19、21、29、33、34、52,解列策略集由原始的227维降低为28维,搜索空间大幅减小。具体网架结构如图3所示,其中灰色圆圈代表分至群Ⅰ的一般节点,黑色圆圈代表分至群Ⅱ的一般节点,空心圆圈代表所求得的公共节点。

表1 负荷节点到两机群最短电抗累积和之差Table 1 Difference between shortest reactance cumulative sums from load node to two unit sets

图3 CEPRI 36节点系统结构图Fig.3 Structure of CEPRI 36-bus system
为将公共节点分配至相应的子系统中以获取初始解列断面,基于实时监测的信息,公共节点与发电机节点故障前后的电压相角如表2所示。
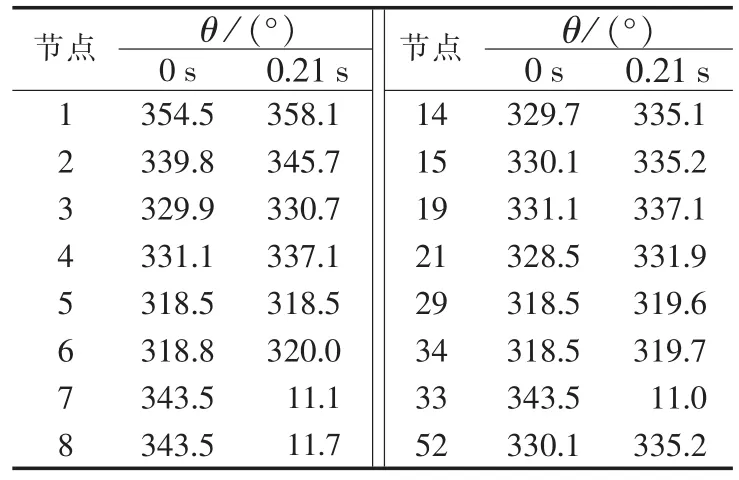
表2 故障前后相关节点电压相角Table 2 Voltage phase angle of related nodes before and after fault
初始子系统和断面如图4所示。
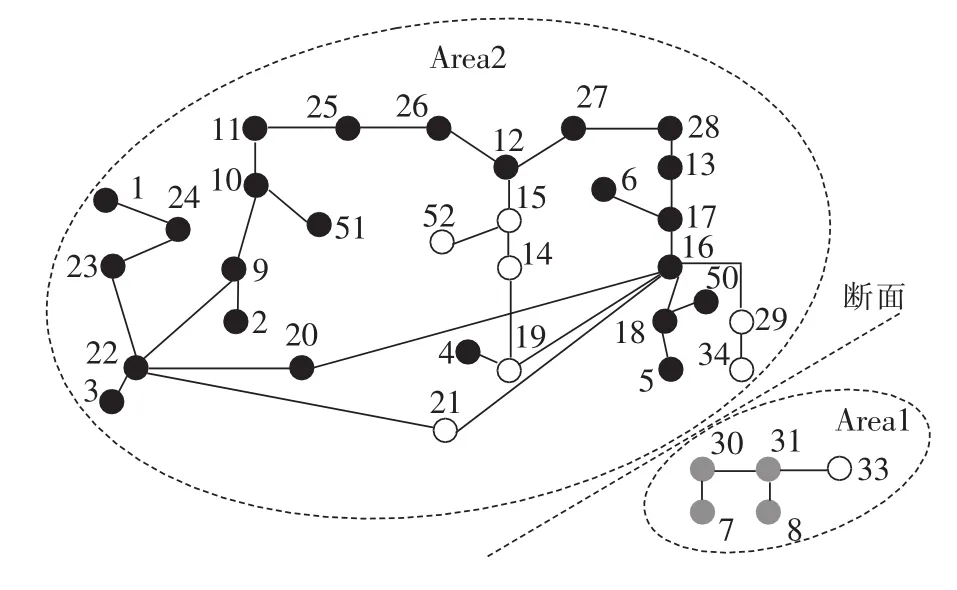
图4 初始断面搜索结果Fig.4 Results of initial islanding surface search
4.1.2 解列断面优化
可知,初步搜索到的解列断面不一定为最终的解列断面。现采用深度优先算法以子系统功率平衡为原则对初始断面做相应的调整。
由潮流计算可知,当解列断面如图4所示,节点{30,31,33}∈Area2 时,Area1 和 Area2 的不平衡功率分别为 0.7391p.u.、0.11p.u。 节点{30,31,33,34}∈Area2时,Area1、Area2的不平衡功率分别为-4.4609 p.u.、5.31 p.u.,依此类推进行校验。结果发现,本文所搜索的初始断面即为最终的解列断面。
在计算时间方面,采用性能为 Intel(R)Core(TM)2 Duo 2.97 GB处理器、4 G内存的计算机进行仿真,初始断面搜索时间为11 ms,解列断面调整时间为4 ms,达到在线运用要求。
4.2 IEEE 118节点系统
以IEEE118节点为例,该系统共包含19台发电机。假设线路80-87发生三相接地故障,发电机{G10,G12,G25,G26,G31,G46,G49,G54,G59,G61,G65,G66,G69}为同调机群Ⅰ,发电机{G80,G87,G89,G100,G103,G111}为剩余机群即失步机群Ⅱ,该系统被解列为2个区域子网。
采用本文第3节所述方法,选取阈值ε=0.05,得到系统的公共节点集为{68,75,77,79,82,104,105,106,107,118},具体结果如图5 所示,图中圆圈含义同图3中。
然后进行暂态特性分析,得到失步机群Ⅰ的发电机节点电压相角平均值,失步机群Ⅱ的发电机节点电压相角平均值°。比较公共节点的电压相角 θj与机群Ⅰ所在集合Va包含节点 68、75、118,失步机群所在集合 Vb包含节点 77、79、82、104、106、107。 以孤岛功率平衡对初始解列断面进行优化,可以得到初始解列断面即为最终解列断面,所需切发电机和负荷量均最小。该系统的搜索时间达23 ms,其中初始搜索时间为17 ms,调整时间为6 ms,满足在线运差的大小,可以得到失步算要求。

图5 IEEE 118节点系统Fig.5 IEEE 118-bus system
5 结论
本文提出一种基于“搜索+优化”的主动解列断面搜索方法。该方法具有以下3点优势:
a.基于Floyd算法求取节点之间的电气耦合强度,完成系统降维处理的过程仅依赖于系统的网络结构,计算复杂度小,满足了解列断面搜索过程快速性的要求;
b.通过节点电压相角之间的暂稳特性寻找系统初始解列断面的过程能适应运行方式的变化,可根据电力实时状况生成最佳简化策略,使得解列断面的确定更加智能化;
c.对初始解列断面进行优化的过程,保证了系统解列后子系统内部稳定性的快速恢复,有效避免了大量切机、切负荷操作。
基于CEPRI 36节点系统与IEEE118节点系统的仿真分析验证了该方法的有效性与正确性。

