基于窗口的自适应中值滤波算法

周萌萌，任子晖，周旋旋

(1.中国矿业大学 信息与电气工程学院，江苏 徐州221008;2.徐州机电高等职业技术学校，江苏 徐州221011)

图像在传输和形成过程中不可避免地会产生各种噪声，这就降低了图像的清晰度。因此，图像去噪是图像处理过程的重要部分。去除噪声的滤波器分为线性和非线性，根据噪声的不同特点选择合适的滤波器。而椒盐噪声的特点是:一种是盐噪声(salt noise)，另一种是胡椒噪声(pepper noise)。盐=白色，椒=黑色。前者是高灰度噪声，后者属于低灰度噪声。一般两种噪声同时出现，呈现在图像上就是黑白杂点。所以针对椒盐噪声的常采用的是中值滤波算法［1］。传统的中值滤波是采用n×n 的模板对当前像素进行滤波，当前像素点的灰度值用选用的模板内的像素点的灰度值的中值替代，此方法虽然能滤去部分噪声，但是却改变了图像像素的灰度值，模糊了图像的细节。因此近年来许多学者提出了诸多的改进方法，如开关中值(Switching Median，SM)滤波［2－4］改进的自适应的中值滤波［5－12］等，这些算法虽然取得了一定的滤波效果，但是还存在许多的局限性和不足。

图像去噪一方面是选择合适的滤波器，另一方面是要合理地检测出噪声，从而更好地保护图像的细节。文献［7］利用窗口3×3，判断是否是疑似噪声点，然后判断疑似噪声点是否是7×7 窗口的噪声点，最后确定准噪声点。文献［8］是通过人为设定的阈值，当窗口的像素点的灰度值与当前像素点的灰度值的差值超过设定的阈值，并计算出超出的像素点的个数，根据超出个数的大小来调节滤波窗口，从而达到滤波效果。文献［9］是首先采用3×3 的模板判断是否是疑似噪声点，再利用像素灰度值序列中两段子序列斜率的差值及模板区域内像素灰度值的均值自适应地判断疑似噪声点是否是真的噪声点。文献［10］采用0°，45°，90°，135°方向的模板进行噪声的检测，降低图像的失真度。文献［11］首先是采用椒盐噪声的0 或1 的特点判断噪声点，再利用可疑噪声点与邻域内其他像素点之间相关性的大小确定准噪声点。这些方法在噪声的检测方面取得了一定的效果，从而达到更好地滤波效果。

本文针对自适应的中值滤波(RAMF)，提出了一种基于窗口的自适应的中值滤波算法。首先，根据椒盐噪声的特点在窗口3×3 中判断是否为极值点，即疑似噪声点，再在窗口5×5 和窗口7×7 判断是否是准噪声点，若是准噪声点，根据噪声的大小，选择合适的最大滤波窗口半径进行中值滤除。若不是，则原值输出。

1 自适应的中值滤方法

1.1 噪声点检测

1.1.1 噪声点的初级检测

椒盐噪声是图像噪声中的一类，它是由图像传感器，传输信道，解码处理等产生的黑白相间的亮暗点噪声。椒盐噪声的表现形式一般是像素点灰度值的最大值或者最小值。如图1 所示，根据椒盐噪声的特点可以通过窗口3×3 来判断当前像素点是否是疑似噪声点。

图1 窗口3×3 邻域像素值

设W3min和W3max是窗口3×3 的像素点灰度值的最小值和最大值，fi，j为窗口3×3 的中心像素的灰度值，若fi，j等于窗口3×3 像素点的最大值和最小值，则fi，j为疑似噪声点，否则，fi，j为信号点。

1.1.2 噪声点的二级检测

窗口3×3 检测出的噪声点不一定就是真正的噪声点，如果把检测出的疑似噪声点都用中值替代，势必会使图像的细节丢失。因此，为了保留图像的更多地细节，需要更精确地检测图像中的噪声。尤其是现代生活中，人们接触到的图像大多都是内容和色彩很丰富，所以，噪声的检测方法对图像去噪是至关重要的。本文采用5×5 和7×7 的窗口对疑似噪声点进行二次检测，标记为W5和W7。W5min和W5max是窗口5×5 的像素点灰度值的最小值和最大值，而W7min和W7max是窗口7×7的像素点灰度值的最小值和最大值。如果fi，j等于W5min和W7min或者W5max和W7max，则疑似噪声点fi，j就是准噪声点;否则，疑似噪声点fi，j是信号点。

通过表1 中的数据对比显示，当随着噪声密度的增加，RAMF 和本文方法的对噪声的漏检率和误检率都越来越小，表明检测噪声的效果也越来越好。但是就本文提出的方法来说，随着噪声密度的增大，漏检率减小，但是没有RAMF 的漏检率小，但是误检率却明显优于RAMF，综合以上的效果，本文方法在噪声检测方面优于RAMF。

表1 RAMF 和本方法的漏检率和误检率

1.2 最大滤波窗口半径的确定

对含有噪声的图像，最大滤波窗口半径根据图像中噪声密度的大小PK 来确定，当PK 较小时，选择合适的较小的最大滤波窗口半径，确保在去除噪声的同时保留了更多细节;当PK 较大时，选择合适的较大的最大滤波窗口半径，加强对图像的去噪能力。根据以上原则，最大滤波窗口半径LK 的选择如下

在同一噪声密度情况下，选取不同的最大滤波半径，通过观察对归一化的均方误差(MSE)和峰值信噪比(PSNR)的值，不同的最大滤波半径对应不同的归一化均方误差(MSE)和峰值信噪比(PSNR)，当归一化均方误差(MSE)较小时，峰值信噪比(PSNR)较大时，选择最佳的最大滤波半径。采用此方法，对图像进行实验得出以上的结论，当噪声密度小于0.3时，选择最大滤波半径为10;当噪声密度处于0.3 和0.5 之间时，选取的最大滤波半径为20;当噪声密度介于0.5 和0.8之间时，用最大滤波半径30 进行滤波;当噪声密度大于0.8时，选取最大滤波半径40，加强去噪能力。

2 算法实现流程

自适应的中值滤波算法流程总体上可以概括为以下:

1)对图像区域的所有像素点用3×3 的窗口进行检测，若像素点的灰度值等于窗口3×3 的极大值或者极小值，则此像素点为疑似噪声点，其他为信号点;

2)对第一步确定的疑似噪声点，进行进一步确认，当疑似噪声点等于窗口5×5 和窗口7×7 的极大值和极小值，则此疑似噪声点为准噪声点，其他为信号点;

3)检测出准噪声点以后，再根据图像中噪声密度的大小，选取合适的最大滤波半径;

4)上述步骤进行完成后，对检测出的准噪声点的灰度值用滤波窗口的中值代替输出，其他信号点原值输出，从而合成新的图像。

3 实验结果与分析

3.1 实验结果评价方法

本文采用主观和客观两种方法对实验结果进行评价:主观方法是对图像滤波后，通过人眼直接观察出滤波效果;客观方法是计算出具体的峰值信噪比(Peak Signal to Noise Ratio，PSNR)和均方误差(Mean Square Error，MSE)的值，通过比较对图像滤波效果进行评价，参数定义如下

式中:X(i，j)和Y(i，j)分别为滤波前后的像素灰度值;mn 为处理图像的大小;max 为滤波前图像像素点灰度的最大值。

3.2 实验结果

本实验采用1 幅大小为512×512 的Lena 图像进行结果验证，图像灰度级为255。使用MATLAB 2012 对各个算法进行仿真分析，包括RAMF、开关中值滤波［4］、自适应中值滤波［13］，并与本文算法进行比较。

对原始图像加入30%和70%的噪声，不同算法的滤波效果如图2 和图3 所示。

图2 30%的噪声图及各种算法滤波效果

图4 显示了噪声密度在10%～90%的变化的情况下，各种滤波算法的滤波效果MSE 和PSNR 的曲线图。

图3 70%的噪声图及各种算法滤波效果

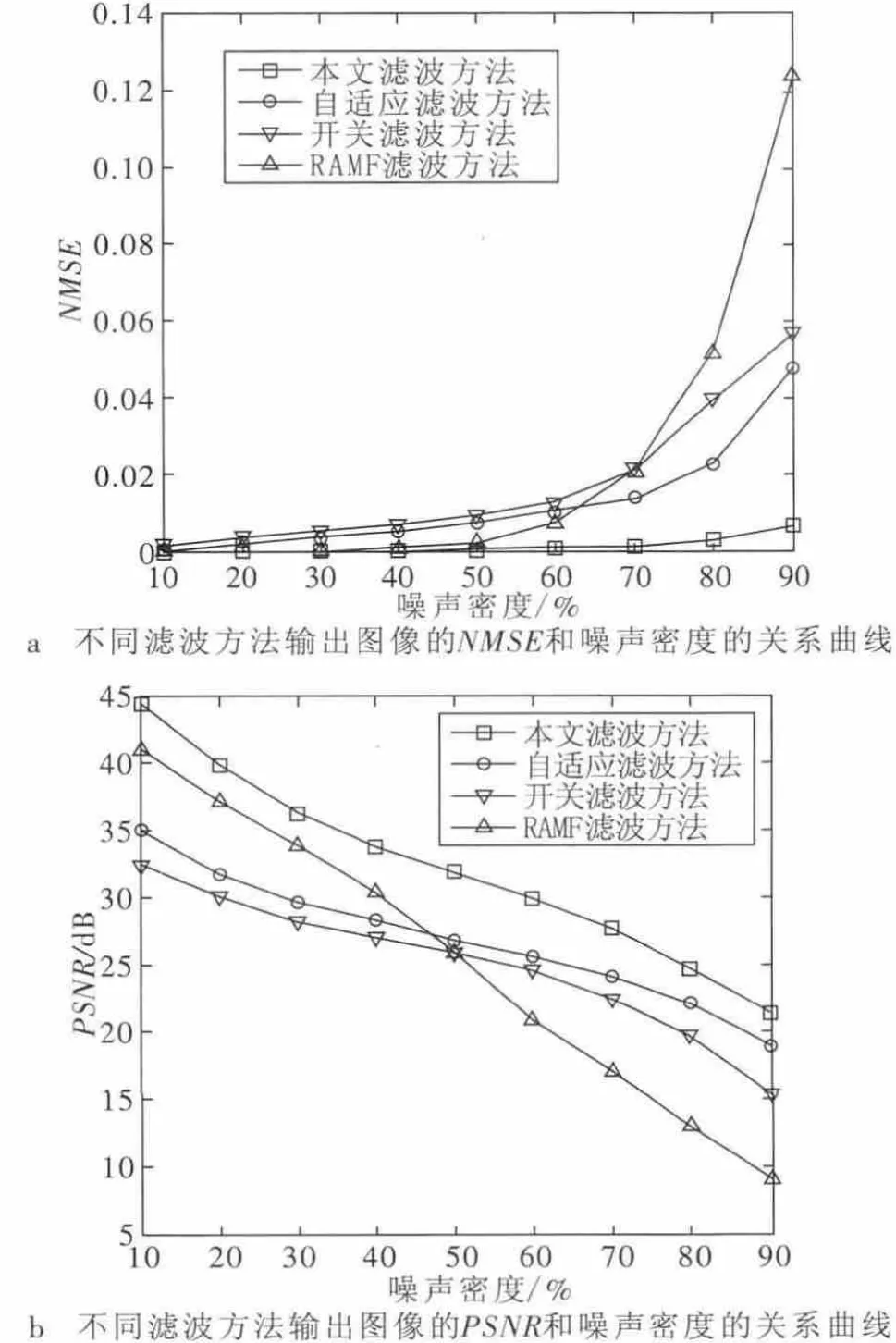
图4 不同噪声水平不同算法滤波的PSNR 和NMSE

从图2、图3 和图4 可以得出:在主观方面，通过图2 和图3 可以直接的观察出在噪声密度30%情况下，自适应滤波方法的滤波效果优于开关滤波，而RAMF 滤波优于自适应滤波方法，本文方法优于RAMF 滤波方法，随着噪声密度的增大为70%时，RAMF 的滤波效果最差，本文的滤波效果最好;在客观方面，通过图4 的NMSE 图和PSNR 图可以观察出不同的噪声密度下，参数的具体数值，通过4 种滤波方法的数据的比较，可以更精确地得出，本文的滤波效果更好，且保护了更多的图像细节。

4 总结

通过对滤波效果的影响因素——窗口的分析，本文提出了基于窗口的自适应的中值滤波算法，该算法首先是利用混合窗口检测噪声，减小了噪声的误检率;然后选择合适的窗口滤波半径。仿真实验结果表明，无论是在主观方面还是客观方面，本文算法在噪声的滤除和细节的保护方面具有很好的效果。

［1］陈初侠，丁勇，刘栎莉.去除椒盐噪声的自适应开关加权均值滤波［J］.计算机工程，2010，36(4):210－212.

［2］苏锋，朱旻芸，杨秋菊.基于自适应开关差值算法的图像椒盐噪声滤波［J］.计算机应用研究，2011，28(2):769－771.

［3］乔坤，郭朝勇，毛东.一种去除椒盐噪声的自适应开关中值滤波算法［J］.计算机应用与软件，2011，28(10):253－256.

［4］曾宪佑，黄佐华，周进朝.基于差分分层噪声检测的开关中值滤波算法［J］.计算机工程与应用，2014(14):176－179.

［5］卫保国.一种改进的自适应的中值滤波算法［J］.计算机应用，2008，28(7):1732－1734.

［6］郭海霞，解凯.一种改进的自适应的中值滤波算法［J］.中国图象图形学报，2007，12(7):1185－1188.

［7］黄宝贵，卢振泰，马春梅，等.改进的自适应中值滤波算法［J］.计算机应用，2011，31(7):1835－1837.

［8］王欢，王修晖.基于阈值判断的自适应中值滤波算法［J］.中国计量学院学报，2011，22(4):382－385.

［9］刘淑娟，赵晔，董蕊，等.基于斜率的自适应中值滤波算法［J］.计算机应用，2012，32(3):736－738.

［10］张彩甜.一种红外图像颗粒噪声自适应滤波算法［J］.红外技术，2013，35(8):502－506.

［11］张洁玉，王峰.基于邻域信息的自适应中值滤波算法［J］.计算机应用，2014，34(7):2010－2013.

［12］阳建华，郑莹娜.一种快速去除高密度椒盐噪声的滤波算法［J］.电视技术，2014，38(13):14－16.

［13］曾宪佑，黄佐华.一种新型的自适应模糊中值滤波算法［J］.计算机工程与应用，2014(17):134－136.