基于灰度梯度和反正切拟合的亚像素边缘检测

吴月波，徐 晨，董 蓉

(南通大学 电子信息学院，江苏 南通226019)

随着图像检测技术的发展，视觉检测的应用研究在各个领域受到了广泛关注。视觉检测原理是以图像为信息载体并从中提取几何参数。在视觉检测领域中，被测图像边缘的定位精度往往直接影响到整个检测的精度。因此，对图像边缘的精确定位具有很大的实际意义。传统的边缘检测算法是利用一阶和二阶微分算子考察图像的每个像素在某个区域内的灰度变化，如Canny 算子［1］、Sobel 算子［2］、LOG 算子［3］以及Laplacian 算子［4］等，这些算子［5］大都为整像素级，形式简单，边缘检测的速度快，但容易受到噪声的影响，定位精度较差。随着对边缘检测精度要求的不断提高，传统的边缘检测算法已经很难满足实际需求。因此，定位精度更高的亚像素边缘检测越来越受到人们的关注。从20 世纪70 年代以来，就有很多学者提出了一些有效的亚像素边缘定位算法［6］。目前常用的亚像素边缘定位算法可以归纳为三类:矩法［7－8］、插值法［9］和拟合法［10］。基于矩的亚像素边缘检测算法形式较为复杂，计算时间较长，但图像的平移不影响边缘的检测;基于插值的亚像素边缘检测算法计算时间较短，具有良好的抗噪性能，但定位精度较低;基于拟合的亚像素边缘算法对噪声有较好的抑制，边缘的定位精度较高，因此，基于拟合的亚像素的边缘检测算法得到了许多人的青睐。

本文提出了一种基于灰度梯度和反正切函数拟合的的亚像素边缘检测算法，它需要提取输入图像的灰度梯度方向，建立灰度梯度直角坐标系，坐标轴正方向由提取的梯度方向来确定，x 轴表示所选择的像素在梯度方向上的坐标，y 轴表示所选择的像素的灰度值，最后利用最小二乘法，采用反正函数拟合提取的图像边缘的灰度梯度，实现亚像素边缘检测。本文算法是一种定位精度更高、检测速度更快的亚像素边缘检测算法。

1 本文算法原理及实现

1.1 算法的原理

本文所提算法是结合Canny 算子和反正切函数拟合图像边缘的灰度梯度实现边缘的精确定位，其算法具体原理如下。

1)Canny 算子［1］是通过求信号函数的极大值来得到图像边缘像素的边缘检测算子。利用Canny 算子获得图像边缘像素的具体步骤如下，见图1。

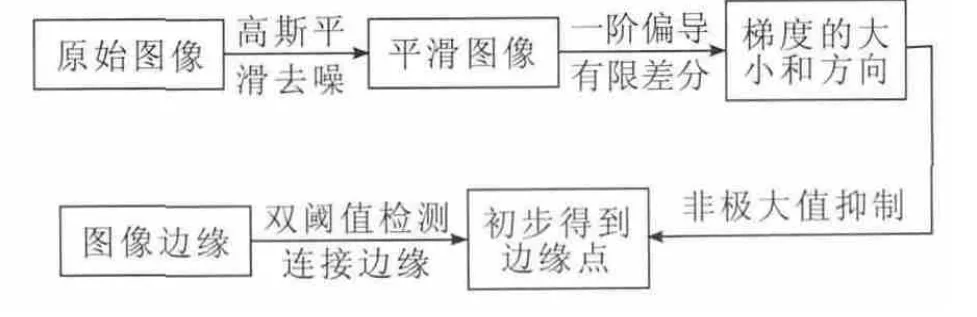
图1 Canny 算子边缘检测

步骤1:将原始输入图像与高斯滤波器进行卷积，以达到平滑图像、去除噪声的目的。

步骤2:用2×2 一阶偏导的有限差分来计算滤波后图像边缘中的每个像素的梯度幅值及其方向。

使用2×2 有限差分模板作为x 方向和y 方向偏导数的两个阵列f'x(x，y)和f'y(x，y)的一阶近似来计算已平滑图像g(x，y)的梯度

由式(1)和式(2)得到一个2×2 正方形有限差分模板，如表1 所示。

表1 2×2 有限差分模板

在表1 中的2×2 正方形内求出有限差分的平均值，用直角坐标到极坐标的坐标转换公式计算得

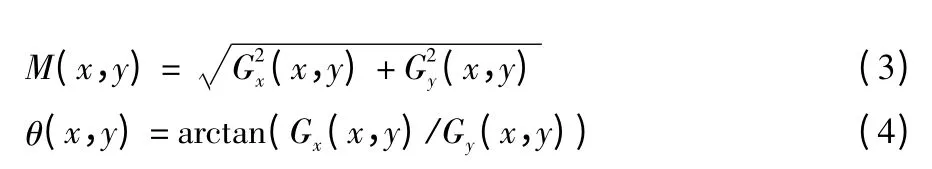
式(3)中M(x，y)表示每个像素的梯度幅值，式(4)中θ(x，y)表示每个像素的梯度方向。

步骤3:为得到图像的边缘，要保留边缘局部梯度幅值较大的点，并且对非极大值进行抑制，最后生成细化的图像边缘。

步骤4:用两个阈值h1和h2(令h1≈0.5h2)分别作用于非极大值抑制处理的图像后，得到图像1 和图像2，图像1 去除了大部分噪声，但却丢失了有用的边缘信息，而图像2 则保留了更多的边缘信息，在图像2 的基础上，补充图像1 中丢失的边缘信息，然后连接边缘，这样就得到了输入图像的初步边缘。

2)由于光学器件的卷积和光的衍射作用，在物空间剧变的图像边缘的灰度值经过光学器件成像后变成了渐变的形式，也就是阶跃边缘变成了渐变的边缘，如图2 所示。

图2 理想边缘和实际边缘模型

反正切函数是数学中一类与常见三角函数类似的函数，它是一个连续、光滑、单调的反三角函数，函数图像如图3 所示，由于反正切函数的图像和边缘模型极其相似，因此，可利用反正切函数作为边缘模型［11］拟合图像边缘实际的灰度分布情况。

图3 反正切函数图像

反正切函数的边缘模型为式中:a1表示将反正切函数趋于的最大值与最小值扩大至原来的a1倍;a2和a3表示反正切函数曲线弯曲的程度，a2和a3的值越大，曲线弯曲的程度越大;a4表示反正切函数在y轴的偏移量。用最小二乘法进行拟合，求出a1，a2，a3和a4，进而得到边缘的亚像素位置。

求图像边缘的亚像素位置的具体步骤如下:

对式(5)求一阶导数得

将式(6)对x 求导并令其导数为0 得

1.2 算法的实现

在算法原理的基础上，算法的实现步骤如下。

步骤1:通过Canny 算子对输入图像进行处理，粗略提取该图像的边缘。

步骤2:对粗略得到的图像边缘逐点的提取图像边缘像素的梯度方向，提取的梯度方向被量化成8 种情况，如图4 所示。当提取的梯度方向如图4 阴影部分所示时，那么此时的梯度方向将会量化在第5 种情况中。基于这个考虑，建立直角坐标系，坐标轴的正方向就可以由边缘像素点的八邻域梯度方向确定，并且这个边缘像素点必须为Canny 算子提取的原始像素点，然后在原始边缘像素点的周围选择一定数量的像素点，将Canny 算子提取的原始边缘像素的横坐标设为0，那么在其周围提取的像素点的坐标也做相应的改变，加入到边缘检测窗口中，如图5 所示。

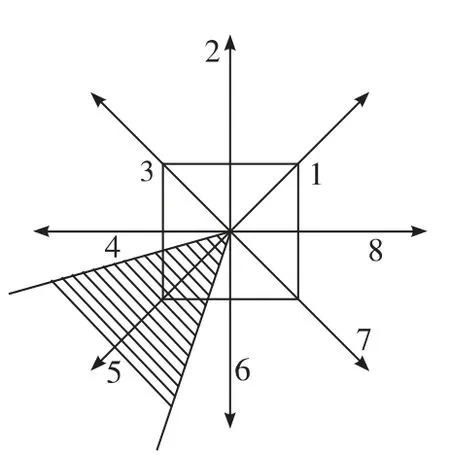
图4 八邻域梯度方向

图5 边缘检测窗口

步骤3:边缘检测窗口中的蓝色方块表示由Canny 算子提取的边缘像素。坐标系的x 轴表示在梯度方向上的像素的坐标，坐标系的y 轴表示所选择的像素的灰度值。

步骤4:建立了灰度梯度直角坐标系之后，使用反正切函数拟合边缘检测窗口中像素的灰度值，并通过最小二乘法处理计算出图像边缘的亚像素位置R=。例如，边缘检测窗口如图3 所示，可以通过图6 所示的函数拟合计算出参数a2和a3的值，进而计算出R=0.131 6。

图6 函数拟合图

2 实验结果及分析

2.1 边缘检测结果分析

为了验证本文算法的稳定性和精确性，采用Microsoft Visual Studio 2008 平台，分别用小波变换法、基于Zernike 矩法和本文所提算法，编程实现对两幅不同图像的边缘检测。第一幅为图像处理常用的Lena 图，第二幅为airplane 图。实验结果如图7、图8 所示。

图7 Lena 图边缘检测结果

对图像边缘检测的评价可以分为主观和客观两种评价标准［12］。主观评价标准是以检测到的图像边缘的视觉效果为根本出发点，并以此来评价图像边缘检测;客观评价标准是以检测到的图像边缘的连续性、有效性等为统一的评价指标，从上面两组图中各种算法对两幅图像的边缘检测结果，通过主观评价，可以明显看出基于小波的亚像素边缘检测算法抗噪性能一般，并且检测到的边缘较少，会出现漏检边缘的现象;

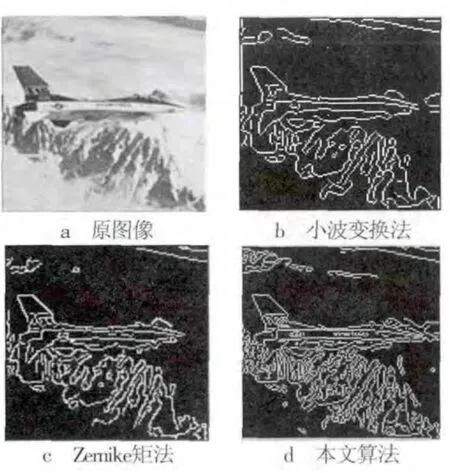
图8 airplane 图边缘检测结果

基于Zernike 矩的亚像素边缘检测算法检测的边缘比较完整，而且边缘连接性较好，但容易受到冗余信息的干扰;而本文所提算法能够更完整、有效地检测图像的边缘，具有更高的抗噪性能，并且可以克服冗余信息的干扰，得到更加平滑完整的图像边缘。

客观评价标准通过统计连接图像的边缘点数、4－连通成分数和8－连通成分数及连通成分比率这些指标对检测到的不同图像边缘进行客观的比较。结果如表2、表3 所示。

表2 Lena 图检测结果

表3 airplane 图检测结果

表2、表3 中A 表示检测边缘的点数，B 与C 分别表示检测边缘图中的4－连通区域数和8－连通区域数。B/A 和C/A分别是4－连通区域数和8－连通区域数在边缘总点数中所占的比例，这个比例越小，说明检测图像边缘的连续性越好。

通过表中的数据可以得出，本文所提算法和其余两种算法相比，B/A 和C/A 这两项指标最小，说明本文算法提取的图像边缘有最好的效果和连续性。

2.2 运算时间结果分析

利用Microsoft Visual Studio 2008 平台，统计本文算法、基于小波的亚像素边缘检测算法及基于Zernike 矩的亚像素边缘检测算法的各个时间点检测到的边缘像素，如图9 所示。然后，计算出这3 种边缘检测算法的平均运算时间，如表4 所示。结果表明，通过与小波变换法及Zernike 矩法各个时间点检测的边缘像素和运算时间进行比较，可以明显地得出，本文算法检测速度更快。

图9 各种算法的边缘检测运算速度

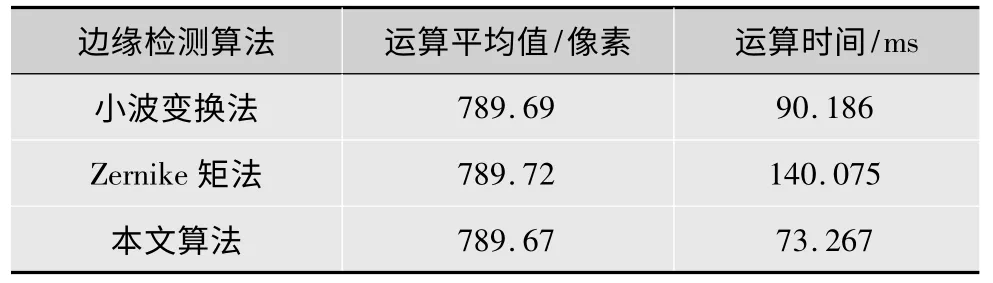
表4 各种算法边缘检测运算时间对比

3 结束

本文提出了一种基于灰度梯度和反正切函数拟合的亚像素边缘检测算法。该算法第一步是用传统的边缘检测算子Canny 算子粗略地提取图像边缘的灰度梯度，第二步是创建灰度梯度直角坐标系，坐标系的x 轴表示所选择的像素在梯度方向上的像素的坐标，坐标系的y 轴表示所选择的像素的灰度值，最后使用反正切函数拟合Canny 算子提取的图像边缘的灰度梯度，并通过最小二乘法计算出图像边缘的亚像素位置。通过与基于小波变换法和基于Zernike 矩法的图像边缘检测算法对比，验证了本文算法定位精度更高，运算速度更快，可有效克服冗余信息的干扰，并且漏检率低，可以准确检测到更加完整平滑的图像边缘。

［1］陈世文，刘越畅.一种基于最小交叉熵的Canny 边缘检测算法［J］.电视技术，2013，37(1):165－168.

［2］SUN Lihua，ZHAO Enliang，MA Long，et al. An edge detection method based on improved sobel operator［C］//Proc.Advanced Materials Research.［S.l.］:IEEE Press，2014:971－973.

［3］ZHANG Jianxin，CHANG Wei，WU Lang.Edge detection based on general grey correlation and LOG operator［C］//Proc. International Conference on Artificial Intelligence and Computational Intelligence.［S.l.］:IEEE Press，2010:480－483.

［4］LUO Yan，LUO Zhiguo. Symmetric positive solutions for nonlinear boundary value problems with φ{symbol}－Laplacian operator［J］.Applied Mathematics Letters，2010，23(6):657－664.

［5］赵玲，张伟. 图像处理中边缘检测算法性能的分析［J］. 科技资讯，2014，12(14):23－24.

［6］孙少红，袁华，张彤. 常用的亚像素边缘检测方法的对比研究［J］. 大众科技，2014，16(176):27－29

［7］付鹏，高晓蓉. 基于矩的亚像素边缘检测算法的对比研究［J］.微计算机信息，2007，23(18):264－265，279.

［8］李永明. 基于Hessian 矩阵的边缘检测方法［J］. 激光杂志，2014，35(5):27－30.

［9］孙秋成，周亚洲，宁闯，等 基于三次样条插值的亚像素边缘检测方法［J］.控制工程，2014，21(2):290－293.

［10］ARCHIBALD R，GELB A，YOON J. Polynomial fitting for edge detection in irregularly sampled signals and images［J］. SIAM Journal on Numerical Analysis，2005，43(1):259－279.

［11］孙维健.一种新的亚像素边缘检测算法［J］. 数字技术与应用，2014(2):126－127.

［12］林卉，赵长胜，舒宁.基于Canny 算子的边缘检测及评价［J］.黑龙江工程学院学报，2003，17(2):3－6.