基于重复博弈的Ad Hoc 网络节点惩罚机制研究

谭 冕，何世彪，李映成，杨 刚，肖利丽

(重庆通信学院，重庆400035)

无线Ad Hoc 网络的正常运作，需要依靠节点间的合作才能保证数据的成功到达目的节点［1］。在通常情况下，理性的参与者受到自身资源的限制，将采取损害网络性能的行为［2］。即便是只存在少量自私节点的网络，其性能也会受损。

目前通过博弈论的方法来解决节点之间的合作问题已经较为普遍。文献［3］认为重复博弈可以作为解决节点的合作问题，但设计的策略不会区分自私者或者合作者是否不具备合作的能力，故此提出了一种增强的基于声誉值的针锋相对模型，不仅依靠惩罚措施，还通过收益鼓励节点参与转发过程。文献［4］提出了一种严厉的针锋相对策略，让自私节点的所有邻居节点对其进行惩罚，并通过惩罚机制参数的调整来观察其对总体收益的影响。文献［5］设计了一种基于重复博弈的全局惩罚模型，邻居节点会通过降低自身的转发概率来惩罚不合作节点。

上述机制存在实现较为复杂的缺点，本文从节点收益的角度，分析网络是否处于一个收敛的稳定状态，并分析不同参数对两种机制收敛的影响。有所区别的是，孤立惩罚机制存在一个孤立期和所有邻居节点一起惩罚自私节点的不合作行为，而通用惩罚机制则是被不合作的节点对自私节点进行惩罚，与其他邻居节点无关。相同的是，两种机制都能对节点的自私行为进行惩罚，减少其收益。

1 系统模型

为方便分析起见，对本文建立的Ad Hoc 网络作如下假设［6］:

1)当前网络G(V，E)由N 个理性的节点构成，其中G 为连通图，V 代表G 的节点，E 代表链路集合。相邻节点间的链路(i，j)∈E，且为双向。

2)整个系统时间由一系列离散的协作时隙t 构成，时隙的长度足够完成数据的传输。

3)用任意两个相邻节点为研究对象，如果一个网络G 中任意两个相邻节点都呈现合作状态，网络整体就会呈现合作状态。网络中任意一组相邻的节点对(i，j)，每个节点都有一定的数据需要对方转发，也要为对方转发一定的数据。

4)所有的数据长度一样，如图1 所示，如果节点i 的数据被邻居节点j 转发，那么就会得到b 的收益，而节点j 得到－c的收益(其中b，c 大于0，且b ＞c)。

5)网络中不存在直接通信的情况，任何源、目节点之间的跳数大于1。

6)时隙内的路由和连接性不变。

7)不考虑网络故障的情况，出现不转发的情况完全是因为节点的自私行为。

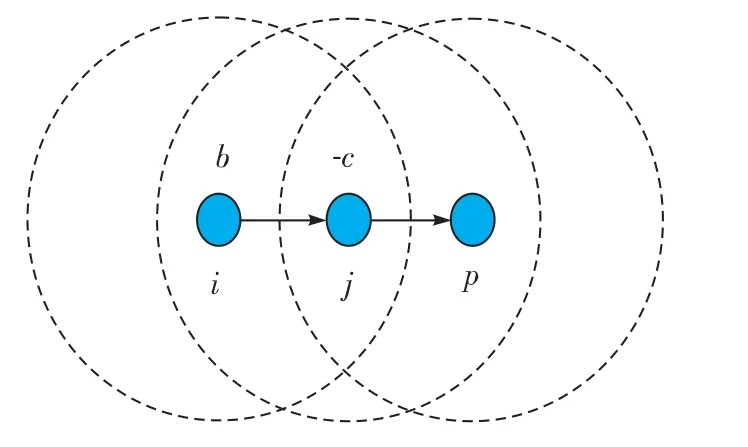
图1 节点转发模型

2 惩罚机制

2.1 重复博弈的节点收益

阶段博弈的节点合作收益不理想，是因为节点不会因为当前时隙的不合作行为而受到惩罚，当阶段博弈不断进行，就会构成重复博弈。参与者会根据当前博弈收益和将来可能的收益，选择适合的决策。

根据重复博弈的原理，节点的收益会在每一个阶段有δ(0 ＜δ ＜1)的折扣率，它代表的是节点的历史行为对未来利益的影响，若其值越大则表示节点更加重视一个长期的利益，根据重复博弈中基于贴现准则的收益评估方式，用Ui代表节点的收益

2.2 孤立惩罚［7］机制

1)合作阶段:初始时刻节点都合作。

2)检测阶段:自私节点i 按照概率k 去合作，当它出现不合作行为时，将会采取持续不合作的策略以获得更大的收益。由于受到网络信道、干扰等因素，其不合作行为不一定会被邻居节点检测到，如果被邻居节点检测到，即转入孤立阶段(被检测到的概率为m)。

3)孤立阶段:自私节点i 的所有邻居节点拒绝转发i 的数据持续r 个时隙(需要说明的是，由于本文仅研究相邻节点对之间的关系，并未讨论目的节点是否收到数据，所以孤立的意思为邻居节点集体拒绝转发i 的数据)，由于理性的节点知道对方的策略，故节点i 在孤立阶段最好的应对策略就是不转发数据。

4)惩罚阶段:自私节点i 需要提供s 个时隙的无偿转发服务，而此时所有邻居节点仍拒绝转发A 的数据。惩罚阶段结束后，节点i 再次回到网络，其不合作行为被遗忘。

2.3 孤立惩罚机制的收敛证明

当理性节点i 决定不合作，若作弊w 次后，才被它周围的邻居节点发现的概率为m(1－m)w－1，此时节点i 的作弊获益为

由前文可知惩罚参数为(r，s)，则节点i 在作弊w 次后被发现，其自私行为所导致的收益的损失为

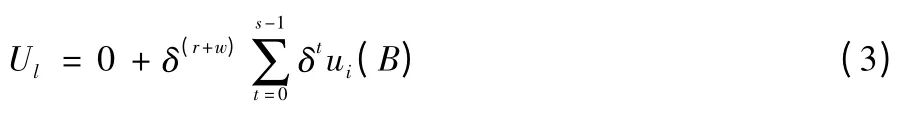
又因为当节点i 经历孤立期和惩罚期，重新加入网络时，它面对的情况是相同的，令Si为当前情景下节点i 选择不合作行为能获得的总收益现值期望，可如下所示

为了消除节点的自私性，需要让节点持续合作的收益至少不小于作弊收益期望Si，即为

当满足上式的时候，自私的节点将更倾向于合作而非背叛。由于δ 和m ∈(0，1)，故式(7)对m 求导为负，当m 越大时，式(7)将越发容易满足，这跟常理相符:当检测概率数值较低的时候，惩罚机制的效率也偏低，作弊节点的收益也就越高。

2.4 普通惩罚［8］机制

1)合作阶段:初始时刻节点都合作。

2)检测阶段:自私节点i 按照概率k 去合作，当它对邻居节点j 出现不合作行为时，将会采取持续不合作的策略以获得更大的收益。由于受到网络信道、干扰等因素，其不合作行为不一定会被邻居节点检测到，如果被邻居节点j 检测到，即转入惩罚阶段(被检测到的概率为m)。

3)惩罚阶段:自私节点i 需要为节点j 提供s 个(s=)时隙的无偿转发服务，而它的数据会被邻居节点j 拒绝转发。惩罚阶段结束后，节点i 重新回到网络，其不合作行为被遗忘。

2.5 通用惩罚机制的收敛证明

类似于孤立机制的收敛证明，节点之间都进行合作的总收益为Vi，如下式所示

节点i 经历惩罚期后，重新加入网络时，它面对的情况相同。假设节点i 因不合作行为而被惩罚后的总收益为，可如下所示

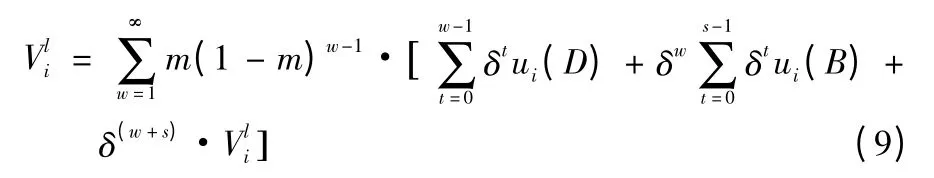
化简可得

为了刺激节点的合作转发，需要满足下式

所以有

当满足上式的时候，自私的节点倾向于合作。

3 仿真分析

在理论分析后，笔者用仿真实验验证上述两种机制的性质。仿真实验共分4 组，分别考察惩罚机制是否稳定、机制下的平均节点收益对比，贴现因子对网络总收益的影响、参数变化对节点收益的影响。

仿真参数如下所示:b=6，c=2，Rm=100，Re=20，N=50，k=0.9，m=0.2，r=2，s=3，T=150，δ=0.9，自私节点数目为5，仿真语言为MATLAB。这里需要说明的是，由于网络中的节点是随机生成的，每个节点的邻居节点数目不确定，且每个自私节点当前时隙按照概率选择不合作行为，由于自私节点是理性的，一旦选择不合作行为就会持续下去，直到被邻居节点发现。

另外仍需注明的是，以下实验为做了1 000 次蒙特卡洛仿真求其平均值得到的，虽然会有误差，但仍可以揭示一些特性。

实验1:考察两种机制随着时隙的变化，其阶段总收益的变化。

如图2 所示，在初始的合作阶段之后，两种机制的阶段总收益迅速下降，逐步稳定下来，可以看出的是由于孤立惩罚机制多一个孤立期的存在，其收敛速度慢于通用惩罚机制，通用惩罚机制大概在第10 时隙收敛，而孤立惩罚机制在第40 个时隙附近接近稳定状态。

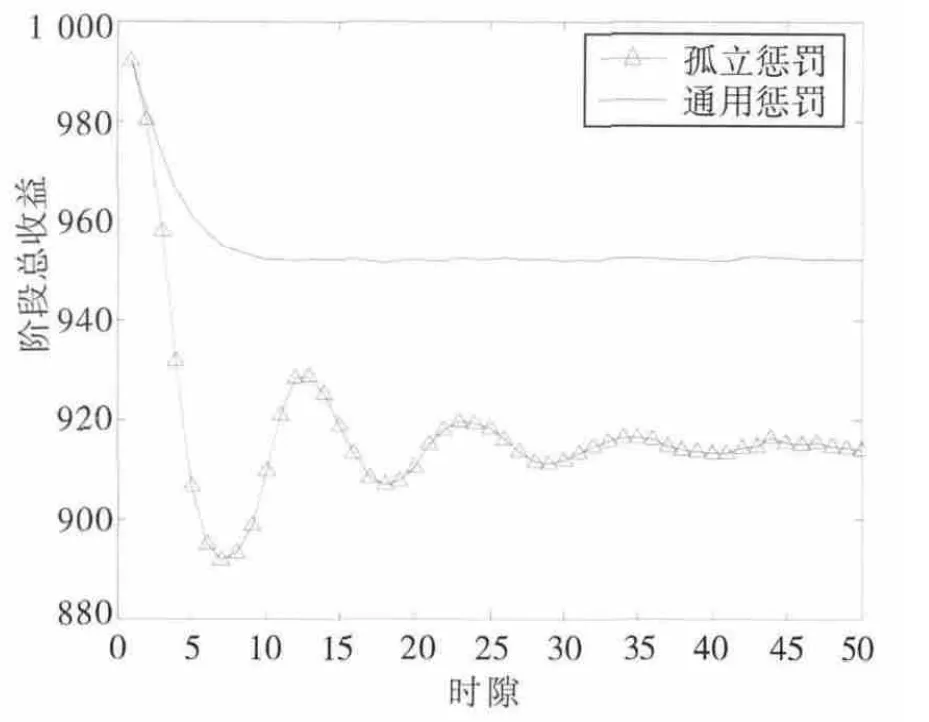
图2 两种机制阶段总收益的变化

实验2:考察两种机制下自私节点和正常节点的平均收益对比。

为方便比较起见，将完全合作机制引入，即正常节点采取完全合作的态度。由于自私节点数目仅为5 个，故其邻居节点数目偏少，在本文中也意味着平均收益偏少，但不影响本实验的对比。图3 为采取孤立惩罚机制，图4 为采取通用惩罚机制，图5 为完全合作机制。

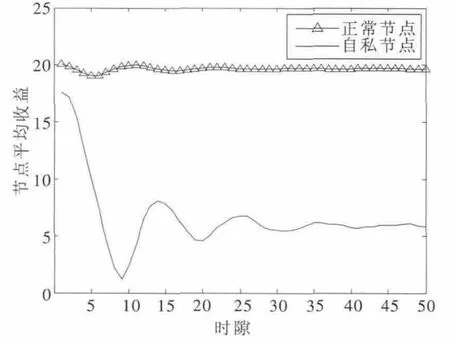
图3 孤立惩罚机制下的平均收益对比

图4 通用惩罚机制下的平均收益对比

如图5 所示，尽管初始正常节点的平均收益高于自私节点的收益，由于自私节点是按照概率来选择不合作行为，但是一旦选择不合作行为就会一直持续下去，而正常节点采取完全合作态度。4 个时隙后，自私节点的平均收益大于正常节点的平均收益。

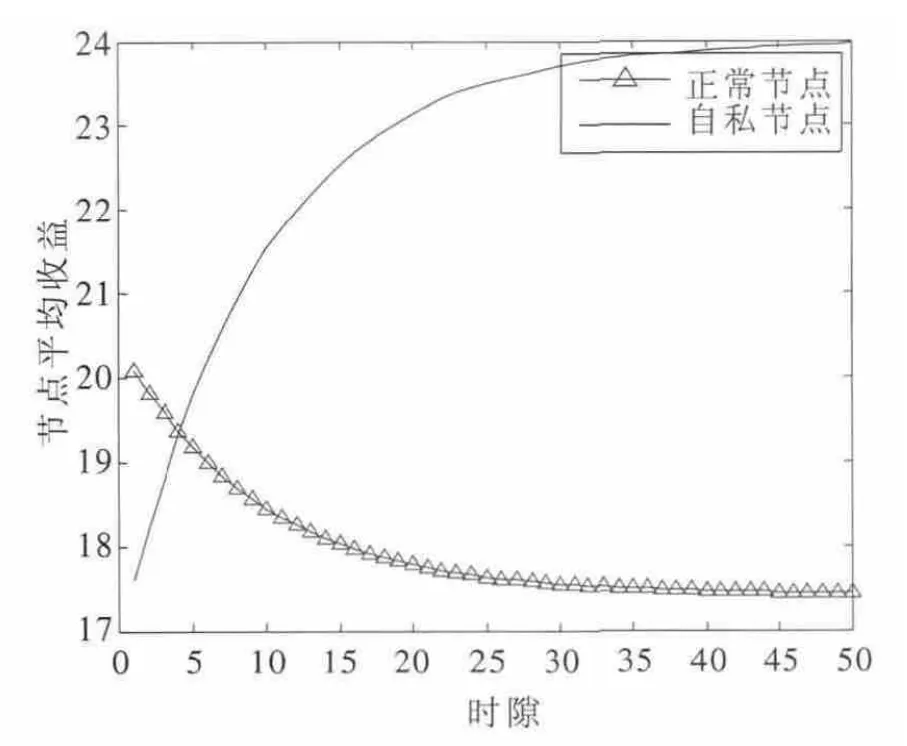
图5 完全合作机制下的平均收益对比

对比图3、图4 可知两种机制都对自私节点进行了惩罚，降低了自私节点的平均收益，但孤立惩罚机制的惩罚力度大于通用惩罚机制，因为其节点收益更少。

实验3:考察贴现因子δ 对两种机制下的网络总收益的影响。

由图6 可知，贴现因子δ 对网络总收益的影响是巨大的，当δ=0.6 和δ=0.9 时，它们之间的收益差接近7 000。当贴现因子较小的时候，两种机制在网络总收益上的差距不大，曲线几乎靠在一起;当贴现因子较大的时候，曲线有一定的区分度。

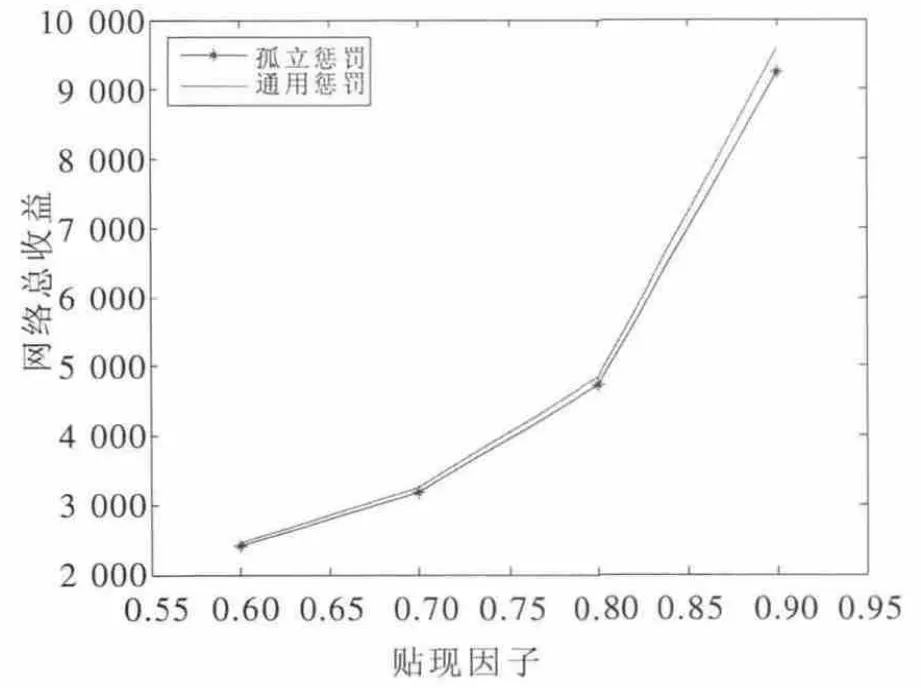
图6 贴现因子对网络总收益的影响

实验4:考察参数变化对两种机制下节点收益的影响。

实验的具体参数变化为惩罚时长s、m－k 数值组合，r－s 数值组合，自私节点数目，共计4 种。

1)惩罚时长s 的变化对两种机制的影响。

惩罚时长s 的大小代表着邻居节点对自私节点惩罚时间的长短，从图7 中可以得知，由于孤立惩罚机制是由孤立期和惩罚期构成，所以惩罚时长单独的变化对其收敛的具体数值影响微弱，但影响了曲线的收敛速度，周期越短，收敛速度越快。从图8 可知，普通惩罚在稳定后的收益值上对惩罚时长较为敏感，随着s 的增加，收益值稳定下降，收敛速度几乎不变。

图7 惩罚时长对孤立惩罚机制的影响

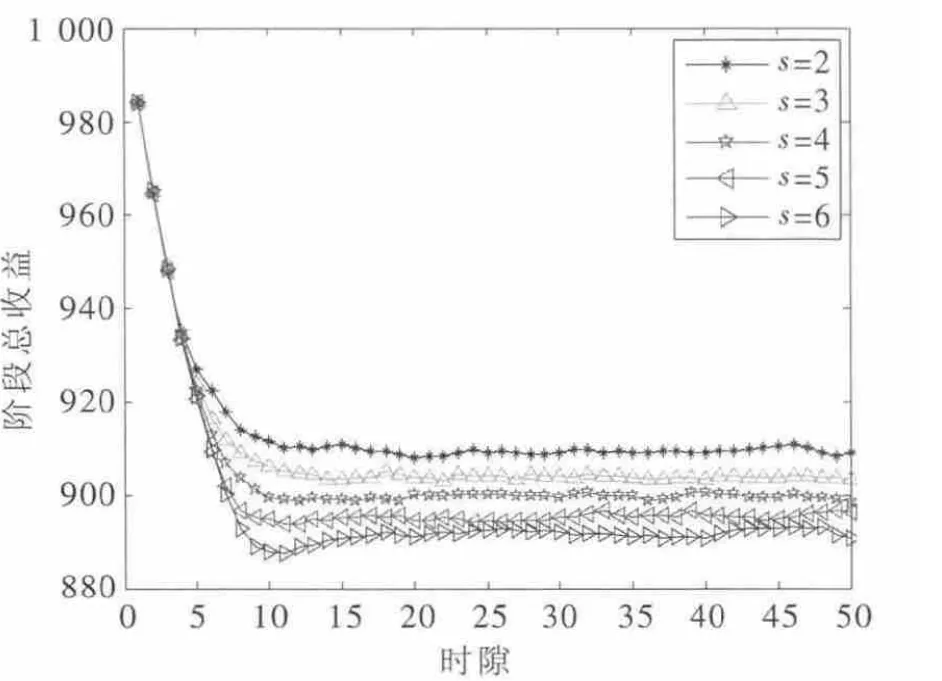
图8 惩罚时长对通用惩罚机制的影响

2)m－k 数值组合对两种机制的影响。

实验共选择了5 组数据，分别是(0.3，0.7)，(0.4，0.7)，(0.3，0.8)，(0.4，0.8)，(0.5，0.8)。

由图9 可知，当m 不变时，k 的增加，会略微增加阶段的总收益值，当k 不变时，m 的增加反而会降低节点的阶段总收益值，这是因为孤立惩罚机制的孤立期不仅降低了自私节点的收益也降低了正常节点的收益的缘故。

图9 m－k 组合对孤立惩罚机制的影响

由图10 可知，对比图9，当m 不变的时候，k 的增加会让整体数值有一个较大的增幅。当k 不变的时候，m 数值的增加，会让通用惩罚机制的阶段总收益值上升，这点和孤立惩罚机制不同。

图10 m－k 组合对通用惩罚机制的影响

3)r－s 数值组合对孤立惩罚机制的影响。

由于孤立期是孤立惩罚机制特有的，所以本实验只能考察对孤立惩罚机制的影响，共选取5 组数据，由图11 可知，当惩罚时长s 不变时，孤立时长r 的增加，使其收益减少。而当孤立时长r 固定时，惩罚时长的增加对其影响主要作用于收敛的速度上，如数组(2，2)、(2，3)或者数组(4，4)、(4，6)所示，也验证了实验4 中1)的结论。

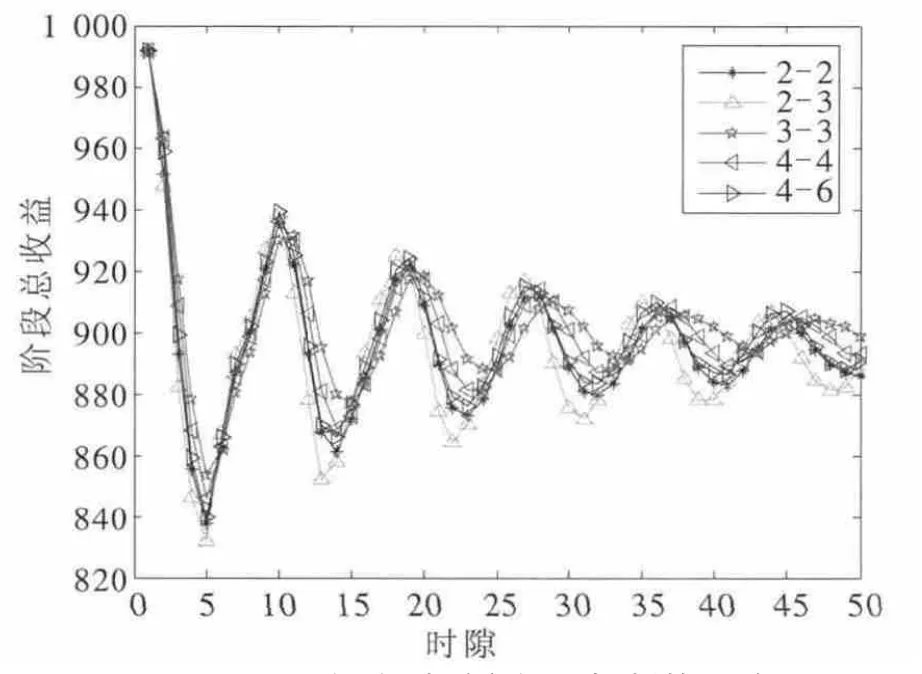
图11 r－s 组合对孤立惩罚机制的影响

4)自私节点数目对两种机制的影响。

从图12 和图13 可知，自私节点数目的增加，阶段总收益稳定下降。由于孤立期的存在使得图12 的收益波动较大，最后仍趋于稳定。与实验1、实验2 对应的是，孤立惩罚机制的惩罚力度较通用惩罚机制更大。

4 结束语

本文中，节点由于具有理性而不愿消耗能量为其他节点转发数据包，为此引入两种惩罚机制，从两种惩罚机制在仿真实验中的对比可以得到一些具体的结论，验证了理论分析。仿真结果证明，两种机制有共同点:对自私节点的不合作行为都会给与惩罚，自私节点个数的增加都会使得收益减小等;不同点:孤立惩罚机制对自私节点的惩罚力度较大，对孤立期时长更为敏感。

图12 自私节点数目对孤立惩罚机制的影响

图13 自私节点数目对通用惩罚机制的影响

［1］DASH M，BALABANTARAY M. Routing problem:MANET and Ant colony algorithm［J］.IJRCCT，2014，3(9):954－960.

［2］RAMTIN A，HAKAMI V，DEHGHAN M. Computer Networks and Distributed Systems［M］.［S.l.］:Springer International Publishing，2014.

［3］AL－DHANHANI A，OTROK H，MIZOUNI R，et al. Enhanced reputation－based tit－for－tat strategy for collaborative social applications［C］//Proc.2013 International Conference on Interactive Collaborative Learning(ICL).［S.l.］:IEEE Press，2013:192－197.

［4］闻英友，赵博，赵宏.基于博弈理论的移动自组网激励机制研究［J］.通信学报，2014，35(4):44－52.

［5］WANG K，WU M，DING C，et al.Game－based modeling of node cooperation in ad hoc networks［C］//Proc. Wireless and Optical Communications Conference(WOCC)，2010 19th Annual. ［S.l.］:IEEE Press，2010:1－5.

［6］王锐，朱青林，钱德沛，等. 一种可容错的覆盖网节点合作激励策略［J］.电子学报，2010，38(2):327－332.

［7］陆音，石进，谢立.基于重复博弈的无线自组网络协作增强模型［J］.软件学报，2008，19(3):755－768.

［8］王博，黄传河，杨文忠，等.Ad Hoc 网络中基于惩罚机制的激励合作转发模型［J］.计算机研究与发展，2011，48(3):398－406.