基于局部线性嵌入稀疏表示的人群行为检测

徐凯航，彭怀亮，章东平

(中国计量学院信息工程学院，浙江 杭州310018)

近年来，人群行为检测已经成为智能视频分析中一个重要的研究热点［1－3］。本文主要是对视频场景中人群异常行为进行检测。人群异常行为的一般定义为:违反群体行为习惯和标准的“反常”行为，即给定一个训练样本集其中Ni是训练样本的个数，i 指的是行为的种类(包括正常行为和异常行为)。aj，j=1，2，…，Ni是训练数据(d 是特征的维数)，它可以是像素、图像块或运动块等。假设测试样本y∈Rd，异常行为检测就是要设计一种分类函数来判断y 的所属类别，即

f:y →{正常，异常(斗殴，恐慌，…)}

为了求解上述问题，需要重点考虑两个问题:行为特征的表示和异常事件的判决。

对于行为特征表示，当前国内外的研究主要是考虑视频序列中人群行为的运动特性，如文献［1］行为特征描述子—多尺度光流直方图用来描述视频序列中行为的空间及时间结构。文献［4］通过对局部时空立方体进行建模，然后利用整个时空立方体统计特征来描述整个场景的异常行为。其他行为特征表示方法，还包括基于背景模型的二值化特征［5］、光流直方图特征［6］、时空梯度特征［7］、社会力模型［8］、混沌不变特征［9］、混合动态纹理特征［10］等。

在异常事件判决方面，最近的研究常把它看成一个分类问题来解决，大多数常用算法通过在训练数据上拟合一个概率模型，将概率接近某一类别的测试样本判别为该类行为。文献［11］提取视频场景中的行为特征，训练各类行为样本的隐马尔可夫模型，进而识别人群异常行为。文献［8］利用社会力模型来提取代表人群的粒子所受的力，然后利用词袋来检测异常。其他的分类模型还有诸如混合高斯模型、混合主成分分析［12］、马尔可夫随机场［13］、潜在狄利克雷分布［14］、条件随机场模型［15］等。

近年来，随着压缩感知的发展，基于稀疏表示的方法被广泛应用于各个领域，如超分辨率［16］、图像去噪［17］、视觉追踪［18］、人脸识别［19］等。基于稀疏性的分类模型假设属于同一类的样本位于同一位置子空间中，任意测试样本能够由一个超完备字典中的少量原子线性表示。众所周知，如果相似的测试样本能够得到相似的稀疏表示系数会大大提高样本的识别精度。但是，传统的稀疏表示模型并没有考虑测试样本的局部流形结构，造成了稀疏分解不稳定问题，即相似的测试样本可能会得到完全不相似的稀疏表示系数。而这种稀疏分解的不稳定性大大影响了分类正确率。

受启发于稀疏表示和流形学习［20－21］方法，本文针对人群行为检测问题提出了一种基于局部线性嵌入［22］稀疏表示的异常行为检测方法，充分考虑了行为样本的局部流形结构。通过在稀疏分类模型中加入一个LLE 正则项，来解决局部流形结构不稳定的问题。并且利用该模型对视频场景中的人群行为进行检测，实验结果表明:文中的局部线性嵌入稀疏表示算法能够有效地提高样本的判别能力，并在人群行为检测中得到较好的实验效果。

1 行为特征获取

通常视频场景中的人群行为特征采用人群周围运动区域的运动信息来描述。本文主要利用变分光流算法初步提取人群运动特征，对视频序列中各帧图像分块，在人群运动前景区域中的块内对初步的运动特征进行处理获取维数较低的行为特征，构建行为特征描述符。

1.1 人群运动区域获取

本文中人群运动区域是通过下面方法获得的，如图1所示。

图1 人群运动区域计算流程

1)Canny 边缘计算:先对图像做高斯卷积平滑，运用梯度值非最大值压抑细化边缘，并用滞后的阈值将与强边缘相连的弱边缘加入边缘图像。

2)运动边缘区域求取:对视频场景图像相邻的两帧的边缘图像做差，以消除静止场景的影响。

3)运动区域获取:在对运动边缘区域求取后，可以得到一个封闭的包含运动目标的边缘线。把每一行中第一个和最后一个边缘点之间的线组成的区域称为水平候选区域，同样竖直候选区域、±45°候选区域也可以得到。通过对这些候选区域求并，并对得到的区域做形态学处理，可以得到基于相邻帧的视频场景运动目标检测结果。如图2 所示。

1.2 改进变分光流法

本文采用在Brox［23］变分光流基础上改进的光流算法。为了增强光流算法对图像灰度变化的鲁棒性，Brox 变分光流算法扩展了梯度一致性假设，并在平滑约束项上，采用分段平滑来代替全局平滑。同时运用多尺度的思想来计算大位移运动的光流。

图2 基于相邻帧的视频场景运动目标检测结果

变分光流算法的能量泛函由数据项和平滑项两部分组成，表示为

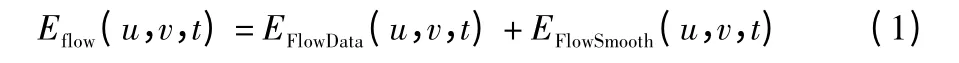
式中，u(x，y，t)和v(x，y，t)为图像中像素点I(x，y，t)光流速度。

在改进变分光流算法中，数据项用多通道图像I［k］取代了标值图像I，还通过能见度项r(x，y，t)来调节

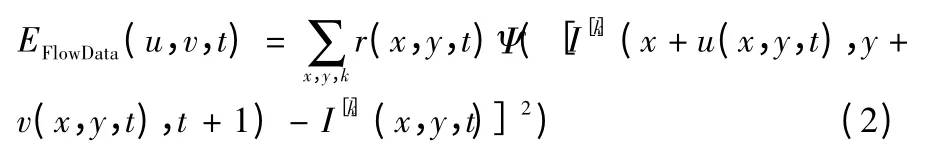
式中:k 是图像通道的总和。图像亮度I，绿减红颜色成分，绿减蓝颜色成分，亮度梯度Ix和Iy作为5 个图像通道来对流量的进行估计。

为了解决小图像梯度不连续流动的问题，在平滑项添加约束项来测量流场的变化。

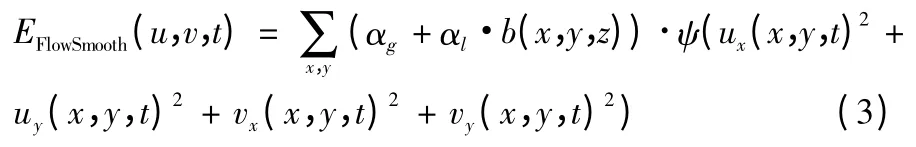
式中:αg是全局平滑因子;αl是一个局部平滑因子，它是被局部平滑b(x，y，z)所调控的。

根据变分计算法，通过最小化能量函数求解u 和v，总的能量函数式先采用固定点迭代转化为线性方程，然后使用逐次超松弛迭代及由粗到细的分层策略可以获取光流场。

1.3 构建行为特征描述符

通过上述改进的变分光流方法，可以计算运动区域光流的变化从而得到三个特征信息:位置、速度和运动方向。为了量化位置信息，把分辨率为360×240 的视频序列分为尺寸为20×20 的小块，并把块的运动方向被量化为5 个方向，当小块中不存在检测到的运动区域时，方向和速度大小都设为“0”。这样视频序列每一帧行为特征维数为18×12×2，整个视频序列特征集就构成了该种行为的特征描述符。特征的描述能力和学习模型复杂性之间的平衡决定了特征的大小。在这里的视频序列中，这样的块选取也是充分考虑行为时长和样本数据量。如图3 所示为行为特征提取过程。

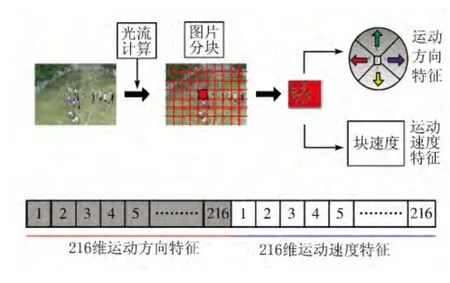
图3 行为特征提取过程

2 行为特征稀疏表示

传统的稀疏表示模型，没有考虑测试样本的局部流形结构，这会导致稀疏分解的不稳定性。这种不稳定性将会极大的降低检测识别精度。本文提出了一种基于局部线性嵌入和稀疏表示的人群行为检测方法，充分考虑了测试样本集的局部流形结构，有效的提高了检测效率。

2.1 基于l1 范数的稀疏表示算法

本节将首先介绍一下传统的基于l1范数的稀疏表示算法。假设有M 个明显差别的类，其中第i 类包含Ni个训练样本并用表示。同一类的特征假定近似于一个低维子空间。换句话说，就是把测试样本y 作为一个m 维的特征。如果y 属于第i 类，那么y 就能够用第i 类训练样本Di的 线性组合来紧凑表示:

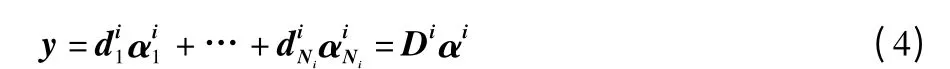
式中，αi是y 在Di上的紧凑表示。要注意的是，在理想情况下如果y 属于第i 类，那么就有αj=0，∀j=1，…，M，j≠i。因此，y 能够通过一个由M 类D=［D1，…，DM］=［d1，…，dN］∈Rd×N组成的超完备字典稀疏表示。y 的稀疏表示可以由式(5)求得

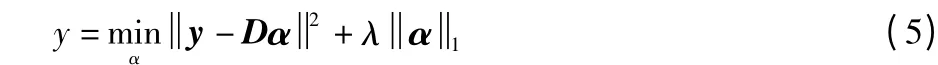
式中:α 是y 在字典D 下的稀疏表示系数;λ 是一个强制稀疏系数。

2.2 基于局部线性嵌入稀疏表示

局部线性嵌入(LLE)是一种流形学习算法，是一种从高维空间非线性映射到低维空间的非监督方法。在LLE 中，基于流形假设:如果样本集是从光滑流形中采样得到的，每一个样本在低维空间中可以用其近邻点线性表示，并保持高维中的局部线性关系不变，可以保留数据集的内在结构。给定数据集，根据LLE，假设yi能够由在同一流形上的测试样本集最近邻线性表示，则其相应的稀疏表示系数αi也能由相应的邻居使用相同的权值的线性组合表示。这种假设是成立的，因为只要每个测试样本和其近邻能够沿着流形的局部线性变化，则这一表示就是稳定的。

基于上述假设，LLE 的二次约束可以定义为

式中:vij表示的是αj的重构权重;N(yi)表示yi的最近邻。yj的选择是根据它是否在yi的k 个最近邻样本内。vij可以通过式(7)得到

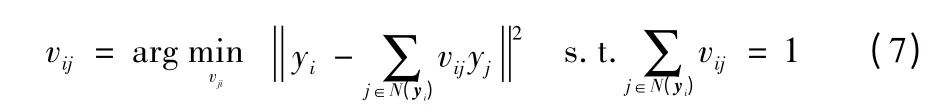
式(6)可以化为如下形式

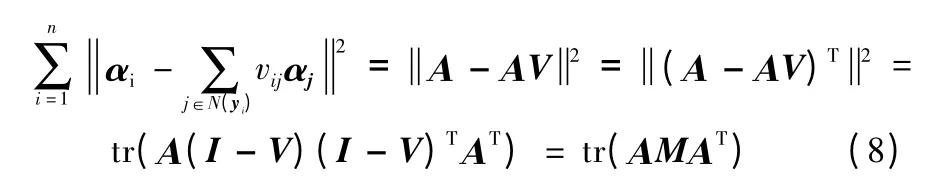
其中，I 是单位矩阵，M=(I－V)(I－V)T是基于LLE 矩阵。V定义为，如果

yj处于yi的k 个最近邻样本内，通过把，其他式(8)并入稀疏表示式中，基于局部线性嵌入稀疏表示可以表示为

其中，λ，λ1为正则化参数。

2.3 稀疏表示系数求解

对于式(9)中的每个αi，可以改写为式中:hi=2λ1(∑j≠i

Mijαj);α(j)i表示αi的第j 个分量。

这里采用文献［24］中提出的Feature－sign 搜索算法求解模型(11)。

算法1 求解式(11)Feature－sign 搜索算法

Input:测试样本yi，字典D，矩阵M，参数K1，λ，λ1

Initialization:α1=0，θ =0(θj∈{-1，0，1})表 示sign(α(j)i)，激活集P={}

Step1:激活

从αi中的0 元素开始，选择

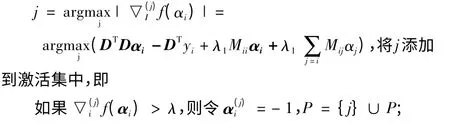
Step2:Feature－sign 搜索

令^D 为D 的子集，即仅仅包含D 中在激活集中的列，â，^hi，^θ 分别为对应的αi，hi，θ 的子集。

通过式(11)求解:

对于解âi到ânewi实施线性搜索，更新âi;

将âi中为0 的项从激活集中移除，并更新θ=sign(αi)。

Step3:最优条件

3 人群异常行为检测

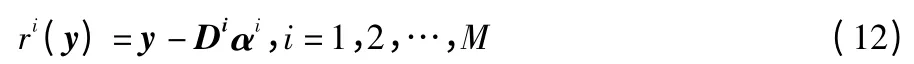
其中，αi中非0 系数表示的是对应类中的原子。y 的类别就可以通过下式中最小残差来确定

然而，在实际中，对训练样本进行标记是十分困难的。因为行为特征的维数一般较大，而样本的个数相对较少，则式(5)就变成了一个超定方程，即:方程的个数大于未知数的个数，会出现无解现象;为了使方程转化为常见的欠定方程，一种方法就是增加D 的维数，也就是需要并入一个d×d 的单位矩阵，则方程(5)转化为

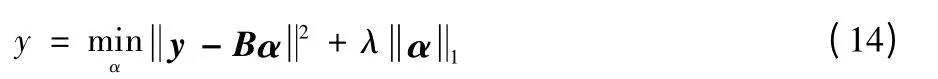
同样的，加入误差矢量的目标函数可以表示为

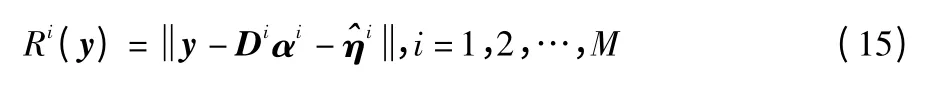
y 的类别就可以通过求解下式的最小残差得到

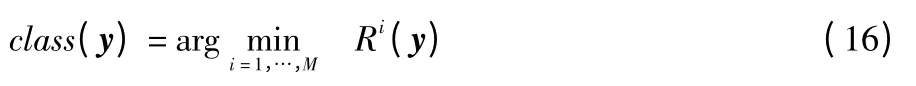
上面介绍了基本的稀疏表示的分类方法，但这些稀疏表示分类算法不能够很好地反映样本的局部流形结构。所以为了提高上述算法的分类性能，受流形学习算法的启发，笔者提出了基于局部线性插入稀疏表示方法来提高各类别的区分度。

本文提出的基于局部线性嵌入稀疏表示的人群行为检测算法归纳如下:

算法:基于局部线性嵌入稀疏表示的人群行为检测算法

Input:训练样本矩阵D=［D1，D2，…，Dk］∈IRm×n，共有M 类;测试样本y∈［y1，y2，…，ym］;

For 1≤i≤m

Step 1:对训练样本集D=［D1，D2，…，Dk］及测试样本y∈［y1，y2，…ym］进行归一化;

Step 2:求解基于局部线性嵌入稀疏表示问题，即通过求解模型(9)求得稀疏表示系数αi。

Step 3:计算残差Ri(y)end for

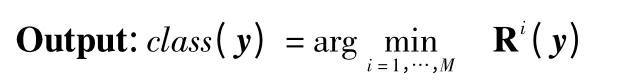
4 实验结果及分析

由于人群异常行为不像人脸识别及指纹识别有大量固定的数据集，所以本实验的实验数据由Sony HVR－V1C 摄像机在校园中拍摄的一组视频，视频中的每一帧图像大小为360×240。视频中包含大量人群交互行为，包含正常、打架、恐慌、踩踏这几种群体行为(见图4)。

图4 视频中的几种群体行为

为了验证本文算法的有效性，使用在相同场景下的描述人群正常、跌倒、踩踏和恐慌的视频序列来测试本文的方法。从拍摄的10 个视频中分别各自抽取如表1 中的4 种行为样本。利用上文中的行为特征提取算法分别获得4 种行为特征集，利用稀疏模型训练得到训练字典。对上述的每种行为特征，选取67%用于训练，剩余的33%用于测试。

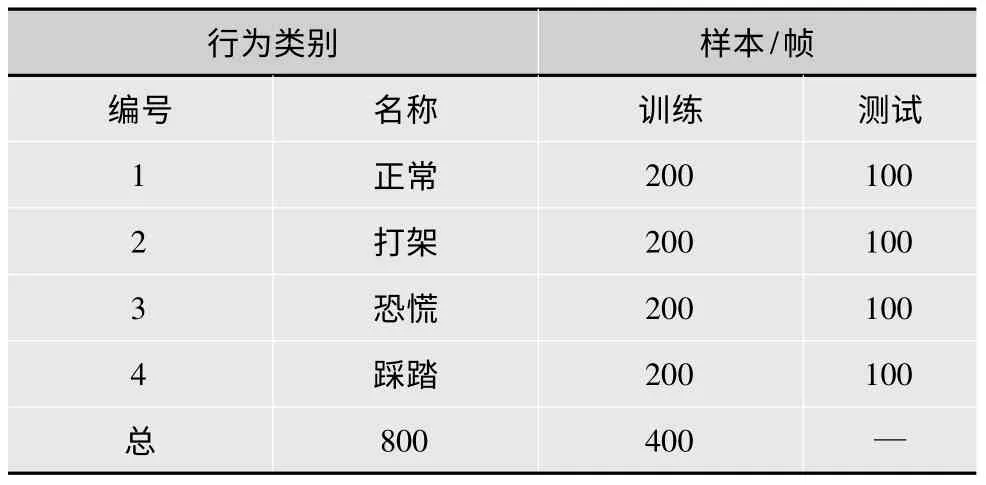
表1 视频序列中的训练和测试样本1

获取稀疏表示字典及测试视频序列的行为特征后，利用局部线性嵌入稀疏分类方法对行为进行分类，这里分别选取200 帧视频序列作为训练样本，这样就可以构成了一个432×800 的稀疏字典，另外分别选取4 种行为各100 帧视频序列用于测试。

如图5 为4 种测试视频序列检测结果。从图中可以看出测试样本可以由稀疏字典中的原子特征重构得到，其重构系数(图5 中的实心点)主要分布在对应该类在稀疏字典中原子所处的位置。

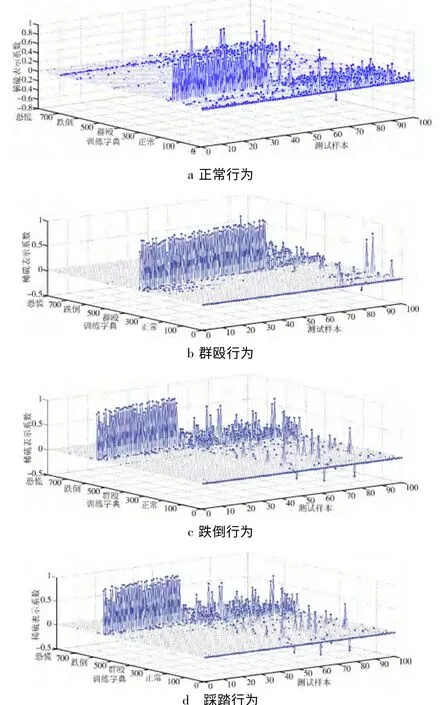
图5 4 种测试视频序列检测结果

为了验证提出的基于局部线性嵌入稀疏表示算法的优越性，实验中和传统基于l1范数的稀疏表示算法进行了比较，表2 是两种算法对4 种测试视频的正确识别率，可以看出基于局部线性嵌入稀疏表示算法(LLE－SR)的正确识别率明显高于传统基于l1范数的稀疏表示(SR)算法。

5 结束语

本文提出了一种基于图像块运动方向及速度的行为特征描述子，该特征能够有效地反映人群行为的空间结构及运动信息，在构建行为特征描述子前，通过对人群运动区域检测，去除背景中噪声运动对行为特征描述子的影响。同时提出了基于局部线性嵌入稀疏表示分类方法，在稀疏表示分类的基础上通过考虑样本的局部流形结构，来解决相似的样本稀疏分解内在的不稳定性。实验结果表明该算法达到了较好的检测效果。本方法的局限是仅仅使用图像块的方向及速度信息，不易区分一些细小的行为，在以后的工作中，将结合一些其他特征完善该算法，对更高层次的行为语义理解进行研究。

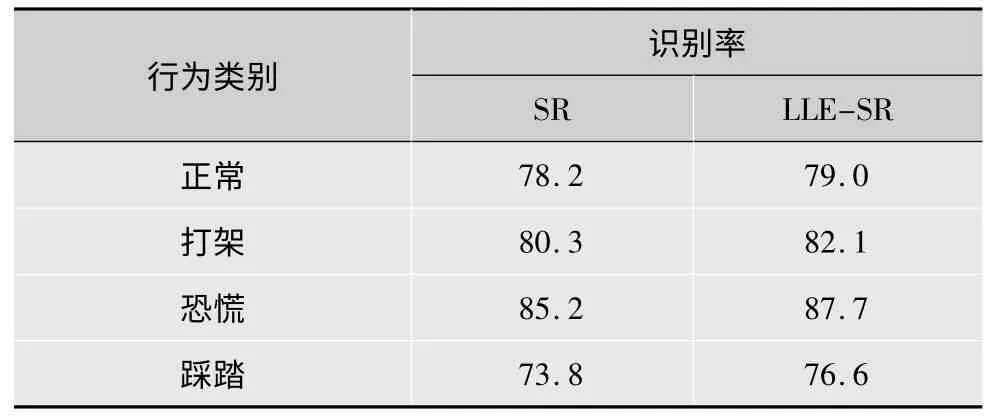
表2 SR 和LLE－SR 算法识别率 %

［1］CONG Y，YUAN J，LIU J. Abnormal event detection in crowded scenes using sparse representation［J］. Pattern Recognition，2013，46(7):1851－1864.

［2］CHO S H，KANG H B.Integrated multiple behavior models for abnormal crowd behavior detection［C］//Proc.2012 IEEE Southwest Symposium on Image Analysis and Interpretation.，Santa Fe，NM:IEEE Press，2012:113－116.

［3］LI C，HAN Z，YE Q，et al.Abnormal behavior detection via sparse reconstruction analysis of trajectory［C］//Proc.2011 Sixth International Conference on Image and Graphics.Hefei Anhui:［s.n.］，2011:807－810.

［4］KRATZ L，NISHINO K. Anomaly detection in extremely crowded scenes using spatio－temporal motion pattern models［C］//Proc.IEEE Computer Vision and Pattern Recognition Workshops(CVPR 2009).Miami，FL:IEEE Press，2009:1446－1453.

［5］BENEZETH Y，JODOIN P M，SALIGRAMA V，et al.Abnormal events detection based on spatio－temporal co－occurences［C］//Proc.IEEE Computer Vision and Pattern Recognition Workshops(CVPR 2009).Miami，FL:IEEE Press，2009:2458－2465.

［6］LI X. HMM based action recognition using oriented histograms of optical flow field［J］. Electronics Letters，2007，43(10):560－561.

［7］KRATZ L，NISHINO K. Tracking pedestrians using local spatiotemporal motion patterns in extremely crowded scenes［J］. IEEE Trans.Pattern Analysis and Machine Intelligence，2012，34(5):987－1002.

［8］MEHRAN R，OYAMA A，SHAH M.Abnormal crowd behavior de-

徐凯航(1991—)，硕士生，主研图像处理与视频分析;

彭怀亮(1988—)，硕士生，主研图像处理与视频分析;

章东平(1970—)，博士，副教授，主研图像处理与视频分析，为

本文通讯作者。tection using social force model［C］//Proc. IEEE Computer Vision and Pattern Recognition Workshops(CVPR 2009). Miami，FL:IEEE Press，2009:935－942.

［9］WU S，MOORE B E，SHAH M. Chaotic invariants of lagrangian particle trajectories for anomaly detection in crowded scenes［C］//Proc. IEEE Computer Vision and Pattern Recognition(CVPR2010).San Francisco，CA:IEEE Press，2010:2054－2060.

［10］MAHADEVAN V，LI W，BHALODIA V，et al.Anomaly detection in crowded scenes［C］//Proc. IEEE Computer Vision and Pattern Recognition(CVPR2010).San Francisco，CA:IEEE Press，2010:1975－1981.

［11］ZHANG D P，LU，Y F，JIANG X H，et al.Abnormal crowd motion detection with hidden markov model［J］. International Journal of Advancements in Computing Technology，2013，5(8):889－897.

［12］KIM J，GRAUMAN K.Observe locally，infer globally:a space－time MRF for detecting abnormal activities with incremental updates［C］//Proc.IEEE Computer Vision and Pattern Recognition Workshops(CVPR 2009). Miami，FL:IEEE Press，2009:2921－2928.

［13］FAIGLE U，SCHONHUTH A.Efficient tests for equivalence of hidden Markov processes and quantum random walks［J］.IEEE Trans.Information Theory，2011，57(3):1746－1753.

［14］WANG X，MA X，GRIMSON W E L.Unsupervised activity perception in crowded and complicated scenes using hierarchical bayesian models［J］. IEEE Trans. Pattern Analysis and Machine Intelligence，2009，31(3):539－555.

［15］PATHAN S S，AL－HAMADI A，MICHAELIS B. Crowd behavior detection by statistical modeling of motion patterns［C］//Proc.2010 International Conference of Soft Computing and Pattern Recognition.Paris:IEEE Press，2010:81－86.

［16］GAO X，ZHANG K，TAO D，et al. Image super－resolution with sparse neighbor embedding［J］. IEEE Trans. Image Processing，2012，21(7):3194－3205.

［17］LI S，YIN H，FANG L.Group－sparse representation with dictionary learning for medical image denoising and fusion［J］. IEEE Trans.Biomedical Engineering，2012，59(12):3450－3459.

［18］MEI X，LING H. Robust visual tracking and vehicle classification via sparse representation［J］. IEEE Trans. Pattern Analysis and Machine Intelligence，2011，33(11):2259－2272.

［19］HE R，ZHENG W S，HU B G，et al.Two－stage nonnegative sparse representation for large－scale face recognition［J］. IEEE Trans.Neural Networks and Learning Systems，2013，24(1):35－46.

［20］LU X，YUAN Y，YAN P.Image super－resolution via double sparsity regularized manifold learning［J］.Circuits and Systems for Video Technology，2013，99(1):1－12.

［21］ZHANG X，YANG Y，JIAO L C.Manifold－constrained coding and sparse representation for human action recognition［J］.Pattern Recognition，2013，46(7):1819－1831.

［22］ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding［J］. Science，2000，290(5500):2323－2326.

［23］SAND P，TELLER S.Particle video:Long－range motion estimation using point trajectories［C］//Proc. 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.New York:IEEE Press，2006:2195－2202.

［24］LEE H，BATTLE A，RAINA R，et al.Efficient sparse coding algorithms［EB/OL］.［2015－01－01］.http://www.researchgate.net/publication/221620168_Efficient_sparse_coding_algorithms._NIPS.