第一性原理对ComAgn(m+n=13)团簇的几何结构和性质的研究

程正富，伏春平，白 静

(重庆文理学院物理系，重庆402160)

1 引言

众所周知，团簇在光、电、磁、力学、催化等物理化学性质[1，2]等方面有着优异的性能.随着团簇科学的发展，吕瑾[2，3]等 Con(n=2 －10)团簇的结构和磁性，并对团簇的结构和磁性能等进行了研究发现磁性嵌埋团簇克服了表面氧化和自聚集效应等困难，但要在我们实际生活中应用，还需解决很多问题，例如团簇大小与组分的控制比例等问题.一些研究者通过蒸发方法所获得的首例无氧化的Fe－Mg(Li)嵌埋团簇，呈现出强的超顺磁性及尺寸效应等特征.继在磁性多层膜和磁性颗粒膜中发现CMR效应以后，又相继在离子团簇束法制备的Fe－Ag磁性嵌埋团簇，以及外延生长的Fe－Ag，Co－Ag嵌埋团簇膜中观察到CMR效应[4－9].基于以上的研究本文采用第一性原理对ComAgn(m+n=13)合金团簇的几何结构、稳定性及磁性等方面进行讨论和研究.

2 研究方法

本论文基于第一性原理在在广义梯度近似(Generalized Gradient Approximation，GGA)下对ComAgn(m+n=13)团簇的结构进行了设计与优化，选择带极化的双数值原子基组和自旋非限制近似求解自洽场[7－10].电子关联为PBE关联，几何结构优化位移量收敛标准取0.05nm，原子间作用力收敛标准取0.02Hartree/nm，能量收敛标准取2×10－5Hartree，自洽场收敛标准取10－6Hartree.计算得到Co－Co，Ag－Ag的键长分别为2.420Å，2.920Å;与实验值2.153Å，2.26112Å进行比较，发现计算值和实验值差异不大，表明我们所选用的方法是合理的[2，3].

3 结果与讨论

3.1 几何结构分析

本文通过对同分异构体进行几何结构优化后计算后，得到了总能最低的ComAgn(m+n=13)稳定几何结构，如图1所示.

图1 ComAgn(m+n=13)团簇的稳定结构Fig.1 Stable structures of ComAgn(m+n=13)clusters

从图1中我们可以看出Co1Ag12团簇是在Ag13团簇的正二十面体的基础上采用Co原子替换中心Ag原子的方法构建起来的，Co2Ag11团簇的构建是在Ag13团簇的中心和顶端分别取代一个Ag原子，其结构具有 C5v对称性;Co3Ag10团簇在Co2Ag11团簇的基础上在其顶端用Co原子取代了Ag原子，从而得到了D2h稳定结构;Co4Ag9团簇是中心占据一个Co原子，其他的3个Co原子分别镶嵌在表面，之间分别间隔一个Ag原子，这种最低的能量结构注定了Co4Ag9团簇的C3v对称性;Co5Ag8团簇中中心Co原子与表面的4个Co原子构成橄榄形模型，其具有C2v对称性;Co6Ag7团簇的结构是Co原子围绕中心Ag原子形成了一个不在同一个平面的六边形，其具有 D3d1对称性;Co7Ag6团簇则是由中心Co原子为连接点和顶端6个Co原子构成的两个正四面;具有D3d1对称性;Co8Ag5团簇则具有D2h结构，8个个Co原子分布于表面;Co9Ag4是在表面以中心原子为对称点的对称结构;Co10Ag3则是由1个中心Ag原子与顶端的2个Ag原子构成的直线取代结构，Co11Ag2与Co2Ag11团簇结构一致;Co12Ag1团簇则是一个Ag原子处于中心的取代结构.

3.2 ComAgn(m+n=13)团簇的稳定性分析

表1中，Co13、Ag13团簇的束缚能、能隙和磁性都存在着很大的区别，Co13的束缚能要比Ag13的束缚能小，这就说明了在构型的正二十面体体系中，Co13要比Ag13稳定的多.众所周知，Co13团簇是属于3d过渡金属团簇，它具有很强的磁性，而Ag13团簇为磁性却很弱.

表1 ComAgn(m+n=13)团簇稳定结构的束缚能、能隙Table1 The binding energies ( Be) and energy gaps(Eg)of the group states for ComAgn(m+n=13)clusters

由图2可知，以Ag原子数增加的方向为横轴，对应团簇的束缚能为纵轴;进行原子束缚能的比较后发现，随着团簇Ag原子数的增加Co原子数的减少ComAgn团簇的束缚能随着增加，表明团簇的物理稳定性随着团簇Ag原子数的减少Co原子数的增加而变的更稳定.

在研究组分不同团簇的相对稳定性时，本文采用了束缚能的二阶能量差分来表征团簇的相对稳定性，公式如下:

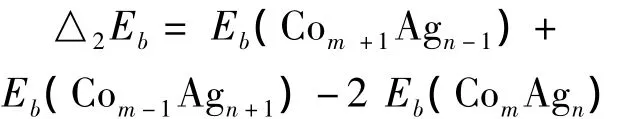
图2 ComAgn(m+n=13)团簇束缚能最随Co原子数减少的变化关系Fig.2 The binding energy changes with the increasing number of Co atom in the ComAgn(m+n=13)clusters

从图3的曲线的变化趋势来看，ComAgn(m+n=13)团簇束缚能的二阶能量差分值都出现不同幅度的波动，分析ComAgn(m+n=13)团簇束缚能的二阶能量差分随着Co原子数增多，束缚能的二阶能量差分在m=2，3，4处，其波动不大，但在m≧4后呈现出明显的奇偶震荡性;当m=6，8，10，12时，ComAgn(m+n=13)团簇束缚能的二阶能量差分出现峰值，表明与近邻团簇相比，Co6Ag7、Co8Ag5、Co10Ag3、Co12Ag1团簇是相对较稳定.

图3 ComAgn(m+n=13)团簇束缚能随着随Co原子数增加的二阶差分Fig.3 The ComAgn(m+n=13)clusters' second order difference energy of binding energy changes with the increasing number of Co atom

图4 给出了ComAgn团簇最稳定结构的能隙(Eg)随团簇中Co原子数的变化规律.从图4可以看出随着团簇Co原子数的增多，ComAgn团簇的能隙变化不大;当n=6时，Co6Ag7团簇的能隙出现峰值，表明Co6Ag7这个团簇较其他团簇有较高的化学稳定性.Ag13团簇的能隙明显比其它团簇的能隙大，说明Ag13团簇的化学活性相对较强.

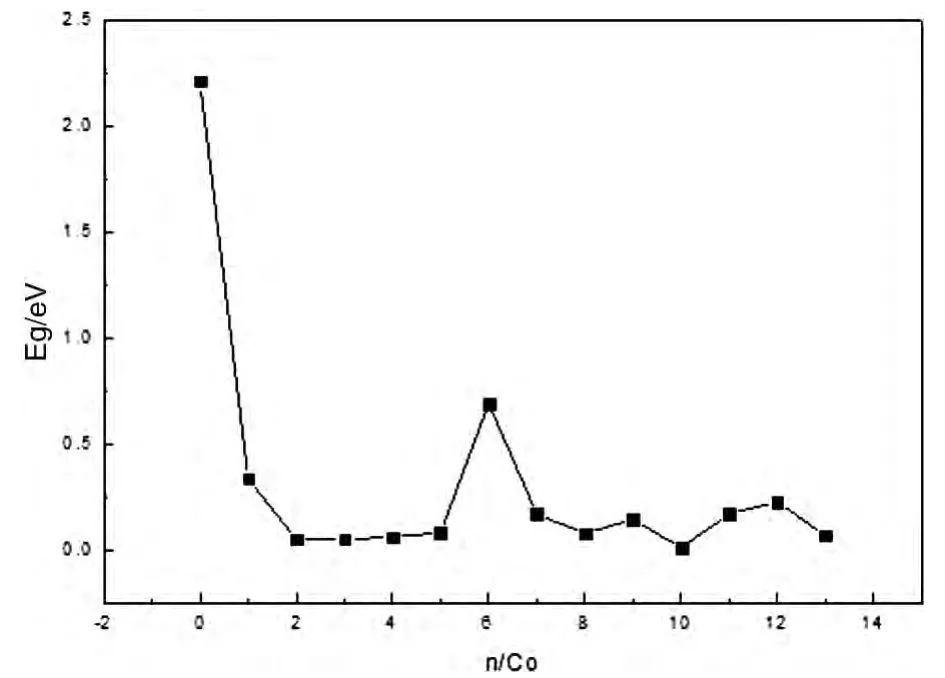
图4 ComAgn(m+n=13)团簇能隙随Co原子数的变化关系Fig.4 The energy gaps changes with the increasing number of Co atom in the ComAgn(m+n=13)clusters

3.3 ComAgn(m+n=13)团簇稳定结构的的磁性分析

我们知道巡游电子自旋交换是铁磁性过渡金属团簇的主要磁性来源，而局域d电子的贡献又起到主要作用，二十面体的高度对称性使得团簇的局域d电子数越多的原子磁性就越强[2]，Dunlap[23]曾指出对于铁磁性物质，对称性越高，团族的磁矩越大;而本论文利用Mulliken布局分析自旋向上态、向下态的电子占据数之差算出磁矩.

表2 ComAgn(m+n=13)团簇稳定结构的磁矩Table2 The magnetic moments of the grou pstates for ComAgn(m+n=13)clusters

通过表2作了ComAgn(m+n=13)团簇的磁距随Co原子数的变化图;从图5中可以看出，体系的磁矩随随Co原子数的变化可以从两个阶段分析:n=1－3随Co原子数的增加，相应团簇的总磁矩是在减小的;而n大于3以后，从磁矩的数

图5 ComAgn(m+n=13)团簇的磁距随Co原子数的变化Fig.5 The magnetic moment changes with the increasing number of Co atom in the ComAgn(m+n=13)clusters

值上看，ComAgn(m+n=13)团簇的磁矩随Co原子数的增加，磁矩大体都是升高的，除Co6Ag7、Co10Ag3两个团簇的磁矩为 －12.868μB，－19.934μB.这种结果可能与团簇的对称性和Co原子数目增加有关，具体成因和规律还需要作进一步的探讨和研究.总之通过磁矩分析表明在正二面体系的ComAgn(m+n=13)团簇中增加Co原子数目有助于磁性的增强.

4 结论

本文利用第一性原理对ComAgn(m+n=13)几何结构、束缚能、能隙和磁性进行了计算研究发现:(1)ComAgn(m+n=13)团簇的稳定结构是基于Ag13正二十面体构建起来的;(2)随着Co原子数增多ComAgn(m+n=13)团簇束缚能的二阶能量差分在m=6，8，10，12时，二阶能量差分出现峰值，表明Co6Ag7、Co8Ag5、Co10Ag3、Co12Ag1团簇是相对较稳定;(3)当n=6时，Co6Ag7团簇的能隙，出现峰值，表明Co6Ag7这个团簇较其他团簇有较高的化学稳定性;(4)通过对ComAgn(m+n=13)团簇磁矩分析说明在正二面体系的ComAgn(m+n=13)团簇中增加Co原子数目有助于磁性的增强.

[1]Ｒen F Z，Wang Y X，Tian F Y，etal. Density － functional study ofZrnCo(n=1－13)cluster structure and their magnetism[J].ActaPhys.Sin.，2008，57(4):2165(inChinese)[任凤竹，王渊旭，田付阳，等.密度泛函理论研究ZrnCo(n=1－13)团簇的结构和磁性[J]. 物理学报，2008，57(4):2165]

[2]LuJ，XuXH，WuHS.Structure and magnetism of Con(n=2 － 10)clusters[J].ActaPhys.Chim.Sin.，2004，20(9):1118(in Chinese)[吕瑾，许小红，武海顺.Con(n=2－10)团簇的结构和磁性[J].物理化学学报，2004，20(9):1118]

[3]LuJ，QinJP，WuHS.Structural，electronic and magnetic properties of ConAl(n=1 － 8)clusters[J].ActaPhys.Sin.，2013，62(5):053101(in Chinese)[吕瑾，秦健萍，武海顺.ConAl(n=1－8)合金团簇结构和磁性质研究[J].物理学报，2013，62(5):053101]

[4]AndzelmJ，Wimmer E.Density functional Gaussian －type－orbital approach to molecular geometries，vibrations，and reaction energies ［J . J. Chem. Phys． ，1992，96: 128.

[5]>Lee C，Yang W，Parr Ｒ G. Development of the Colle>－Salvetti correlation － energy formula into a functional>of the electron density［J］. Phys. Ｒev. B，1988，37:785.

[6]Lacaze － Dufaure C，Blane C，Mankowski G，etal. Density functional theoretical study of Cun，Aln(n=4～31)and copper doped aluminum clusters: electronic properties and reactivity with atomic oxygen ［J］. Surf.Sci. ，2007，601( 6) : 1544.

[7]ZopeRR，Baruah T.Conformers of Al13，Al12M，and Al13M(M=Cu，Ag，andAu)clusters and their energetics[J].Phys.Rev.A，2001，64:053202.

[8]Fournier R，ChengJBY，WongA.Theoretical study of the structure of lithium clusters[J].J.Chem.Phys.，2003，119:9444.

[9]Dunlap BI.Symmetry and cluster magnetism [J].Phys.Rev.A，1990，41(10):5691.

[10]FuCP，XiaJH，XiaoXY.First－principles study of structures and properties of AlmSin(m=1，2;n=1－6)clusters[J].J.At.Mol.Phys.，2013，30(1):84(in Chinese)[伏春平，夏继宏，肖绪洋.第一性原理对AlmSin(m=1，2;n=1－6)团簇结构与性质的研究[J].原子与分子物理学报，2013，30(1):84]