模糊综合评估法在地铁超深基坑施工风险评估中的应用

上海建浩工程顾问有限公司 上海 200030

1 概述

近年来，随着大城市轨道交通网络的逐步建成，地下换乘车站逐渐增加，基坑开挖深度越来越大，地铁超深基坑所占比例逐渐提高。

深基坑工程施工受施工区域水文地质条件、施工工艺、周边环境等多重因素共同影响，施工难度高，风险概率大，一旦发生事故将产生巨大经济损失和严重社会影响，因此，施工前有必要对工程进行风险评估，以便于做好风险全过程控制与管理[1,2]。

目前，风险估计的方法很多，包括专家调查法、层次分析法、事故树法、模糊综合评估法、神经网络法等[3]。前3 种方法简单方便，应用较为广泛，后两者计算过程复杂，目前应用相对较少。而模糊综合评估法则是根据模糊数学的隶属度理论将定性评价转化为定量评价，即用模糊数学方法对受到多种因素制约的事物或对象作出总体评价，具有结果清晰、系统性强等优点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。因此，本文选择用模糊综合评估法对地铁超深基坑施工进行风险估计。

2 工程概况

某地铁车站为地下6 层岛式站台结构，其中标准段长约150 m，宽度约25 m，开挖深度30 m，采用框架逆作法施工。围护结构采用地下连续墙复合衬砌结构，地下连续墙厚1 200 mm，主体结构墙深为55 m，竖向设10 道支撑，第1道为混凝土支撑，第4、6、8道为下3、下4、下5层板框架逆作，其他为钢支撑，其中第5道钢支撑需移位，除第9、10道钢支撑为φ800 mm钢支撑外，其他均为φ609 mm钢支撑。

场区地下土层⑥层受第⑤1c层切割缺失，而⑦层埋深比较深。上部均为饱和黏性土，基坑影响深度范围内揭露的第⑦1层砂质粉土层属第1承压含水层，⑨1层属第2承压含水层。

基坑周边保护建筑物众多。其中，标准段西侧距离某公寓约16 m；北端头井距离某商厦最近距离为14 m；东南侧地下5 层附属结构距离某高层建筑最近为5 m。经勘查，周边地下重要市政管线及地面架空线比较多，场内有1根φ1 m的上水管横穿地铁车站，埋设深为1.2 m，因此，施工时需要重点保护。

3 风险源识别

风险源识别是指在风险事故发生之前，结合工程实际情况系统地认识所面临的各种风险以及分析风险事故发生的潜在原因。本工程难点主要在于：

1）场地地处繁华市中心，场地范围内原建筑密度大，且在城市历史发展进程中经历了多次重建、改建和扩建，地下障碍物颇多，埋深范围大。北侧施工范围内有多座人防沉井等障碍物，外包φ10 m，底板埋深约15 m。地下连续墙施工之前需进行清障处理，因此对导墙的施工要求极为严格。

2）地下连续墙厚度1.2 m，深约55 m，施工中对成槽设备性能、槽壁稳定要求极高，钢筋笼质量最大约65 t，整体吊装对钢筋笼制作的整体刚度和吊装机械的要求也都相当高，如何组织好地下连续墙施工是本工程的一个关键点。

3）由于基坑开挖深度比较深，因此对自身变形控制的要求也高。

4）建设场地地下分布有⑤1c层、⑦层等粉砂土，在基坑开挖时易产生流砂及管涌现象；同时存在埋深7.2 ～11.3 m的第⑦层粉砂层承压水，同时基坑降水又会对周边环境产生明显不利影响，实施难度大。

综合以上因素，运用专家调查法，识别出本工程的施工风险源如表1所示。

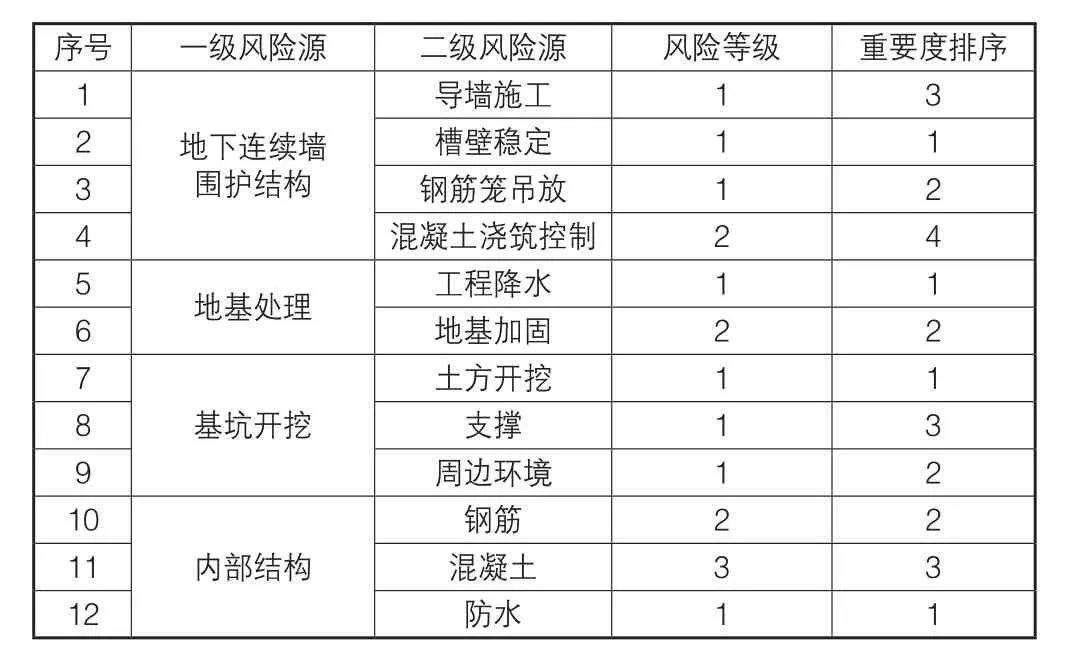
表1 施工风险源

4 基于模糊综合评估法的风险评估

模糊综合评估法应用模糊数学方法对目标对象所涉及到的因素进行单一评判，然后综合各方面的情况，对目标对象给出综合评判。模糊综合评估法的步骤分为四步，具体如下[4-6]。

4.1 第一步：建立因素集和评判集

设U=｛u1，u2…，un｝为n种因素构成的集合，称为因素集；设V=｛v1，v2…，vm｝为m种判断所构成的集合，称为评判集。

评判集表示被评价对象对各指标等级隶属程度的信息，体现了评判的模糊特性。在多因素的风险综合评估体系中，风险指标体系的建立是前提条件，是整个评估问题的核心，风险因素指标的选取应结合风险的识别和单个风险因素的评估结果来进行。因素集用于确定评价因素体系，解决从哪些因素来评价客观对象的问题。在复杂的风险评估系统中，需要考虑的因素往往很多，因素还要分成若干层次，形成评估树状结构，对各层次的因素划分评估等级。

各层次划分的评估等级数应相同、上一层次与下一层次划分的评估等级要有一一对应的关系，以便数学处理运算，并确定各因子的隶属函数，并以此求得各层次的模糊矩阵。

根据《城市轨道交通地下工程建设风险管理规范》（GB 50652—2011），建立评判集V＝｛v1，v2，v3，v4，v5｝，等级值取为V＝｛5，4，3，2，1｝。根据表1识别出的施工风险源，一级风险源包括4 个因素：地下连续墙围护结构、地基处理、基坑开挖和内部结构，每个一级风险源又可分解为若干二级风险源，具体如表1所示。

4.2 第二步：建立综合评判矩阵

通过建立模糊隶属函数的方法生成综合评判矩阵R=（rij）n×m。其中，rij表示因素ui对评判vj的隶属度，ri·=（ri1，ri2，…，rim）表示因素ui对评判集V的隶属向量，由n个隶属向量生成判断矩阵R=（r1·，r2·，…，rn·）T。

在普通集合理论中，任何一个元素或者是属于某集合U，或者是不属于它。而在模糊集合理论中，由于存在着模糊性，论域中的元素对一个模糊子集的关系就不再是“属于”和“不属于”那么简单，其对该模糊子集的隶属程度大小即为隶属度，取值在0～1之间。v1～v5隶属函数和参数的选择如下。

v1的隶属函数采用降半梯形分布函数，参数a1取1，a2取3，即：

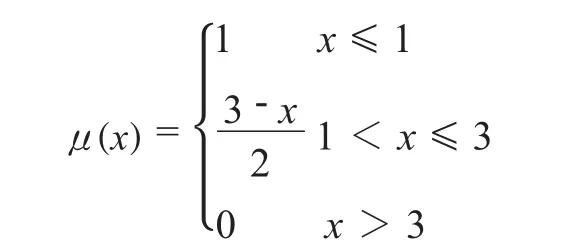
v2、v4的隶属函数采用尖Γ分布函数，参数a分别取2，4，k取2，即：

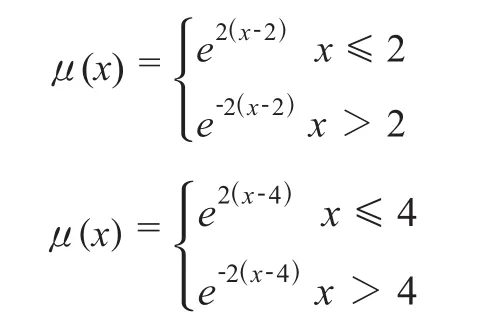
v3的隶属函数采用降半梯形正态分布函数，参数a取3，k取2，即：

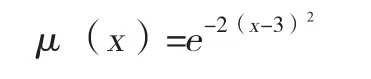
v5的隶属函数采用升半梯形分布函数，参数a1取3，a2取5，即：

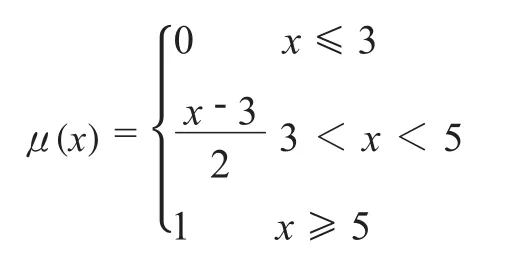
根据地质条件和施工方法参数综合评估，通过专家调查，得出二级风险源的风险等级如表1。

现以工程中地下连续墙施工为例，将单因素风险等级值依次带入v1～v5的5 个隶属函数，得到一个3 行5 列的模糊变换矩阵：

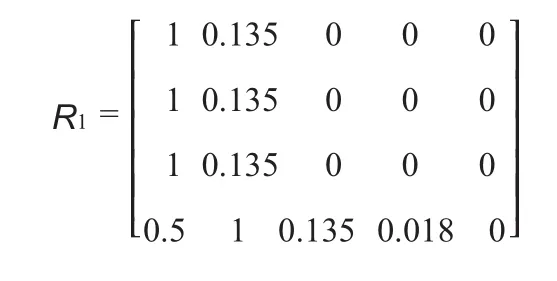
4.3 第三步：综合评判

对于因素集U上的模糊集A=（a1，a2，…，an），通过R变换为评判集V上的模糊集：

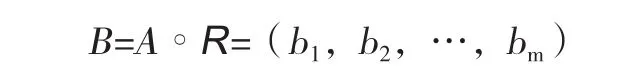
以地下连续墙施工为例，根据层次分析法，得到权重向量：

A1=[0.16 0.467 0.278 0.095]

合成运算采用加权平均，计算结果为：

同理，求得B2=[0.833 0.424 0.045 0.006 0] ；

4.4 第四步：计算综合评判值

N=W。B

其中W=[w1，w2，…，wm]是评判集的权值分配向量，按照普通矩阵的乘法，可得到综合评判值。

假设4 个一级风险源权重相当，分别取0.25，则模糊评价向量

根据“最大隶属度原则”，判断该地铁超深基坑总体风险等级为一级。故在基坑施工过程中，必须采取严格控制措施，避免风险事故的发生。从安全管理方面来说，可以在关键节点进行条件验收，对施工前的安全条件进行梳理和验证，若施工准备不充分或达不到要求者不得开工，真正做好风险预控，杜绝重大安全事件发生。从质量控制方面来说，需要做好一个分部或分项工程的关键节点条件验收，对上道工序进行验收检查，对下道工序做好预控检查。

5 结语

从以上模糊综合评估的过程可以看出：模糊综合评估结果本身是一个向量，而不是一个单点值，并且这个向量是一个模糊子集，较为准确地刻画了对象本身的模糊状况，提供的评价信息比其他方法更全面更系统。

应用模糊综合评估法进行工程风险评估的关键在于2 个方面：一是风险源识别。不同深基坑工程风险源差别很大，要结合工程特点和难点确定；二是隶属函数确定。在进行模糊评估时，如何确立各个因素对应于各个评估等级的隶属程度的大小，是整个评估能否进行的关键。隶属函数选择要结合评估参数的实际分布情况确定[7,8]。