一种适用于多直流馈入系统的限流措施优化配置方法
杨 冬 ,周勤勇 ,刘玉田
(1.国网山东省电力公司电力科学研究院,山东 济南 250002;2.中国电力科学研究院,北京 100192;3.山东大学 电网智能化调度与控制教育部重点实验室,山东 济南 250061)
0 引言
电网联系日趋紧密及大容量发电机组接入使受端电网短路电流超标问题日益严重。各种限制短路电流措施在电网中的应用日趋成熟,因此采用数学方法对其进行综合优化具备较好的可实施性。文献[1]提出了一种限制短路电流的电网结构优化调整算法。文献[2-5]对故障限流器的安装位置、数量及阻抗值进行优化。文献[6]利用线性化技术对开断线路和安装限流电抗器进行综合优化。文献[7]将限流措施配置问题描述成一个混合整数规划问题。文献[8]在考虑潮流约束的情况下,建立了一种限流措施多目标优化模型。文献[9]基于网络分析法建立了限流方案的综合评价模型。
多回直流馈入是我国受端电网的另一个重要特征。理论分析和仿真计算发现,多直流馈入受端电网面临的最大风险是电压稳定问题[10-13]。文献[14]提出了交直流系统网架结构评价的3种指标,采用多馈入短路比作为电压强度指标,用于评估受端系统对多回直流的电压支撑能力。文献[15]指出短路电流控制方案与多直流馈入电网电压稳定性之间具有较强相关性。文献[16]提出了一种基于故障限流器的电网动态分区技术,在故障情况下利用故障限流器将电网自动分裂,从而有效提升多直流馈入电网的稳定水平。
限制短路电流会改变受端电网的拓扑结构,一方面降低了直流换流母线短路容量,另一方面改变了各直流逆变站间的电气距离,可能使多馈入短路比增大,也可能使其减小,从而影响交流系统对多回直流的支撑强度。因此,对于多直流馈入电网的短路电流超标问题,存在既可以将短路电流控制在合理范围内,又能使多馈入短路比保持在较高水平的限流措施配置方案,需要通过建立多目标优化模型来求取。目前针对限制短路电流优化的研究大多根据投资成本进行单目标优化,未见有考虑限流措施对多直流馈入系统影响的相关文献。
针对协调解决短路电流超标和多回直流相互影响问题,本文提出了一种适用于多直流馈入系统的限流措施优化配置方法。基于多馈入短路比的定义,理论推导了限制短路电流措施对多馈入短路比的影响。在此基础上,提出了能够反映限制短路电流成本及效果、网络联系紧密程度以及受端系统对多回直流支撑能力的目标函数。采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ),结合支路筛选策略,寻找Parero最优的限流措施配置方案。
1 多馈入短路比分析
1.1 多馈入短路比定义
考虑交流系统短路容量、多回直流输电容量以及各直流逆变站间的电气耦合关系,国际大电网会议组织(CIGRE)提出了多馈入短路比的定义[17]:
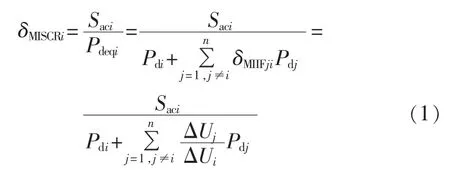
其中,δMISCRi为第i回直流的多馈入短路比;Saci为第i回直流的换流母线短路容量;Pdeqi为考虑其他直流影响的等值直流功率;n为直流回数;Pdi、Pdj分别为第i、j回直流的额定功率;δMIIFji为多馈入相互影响因子,它的定义为当在第i回直流的换流母线上施加微小的无功扰动时,第j回直流的换流母线电压变化量ΔUj与第i回直流的换流母线电压变化量ΔUi的比值。
多馈入相互影响因子是决定多馈入短路比定义的关键,它能够反映各直流逆变站间的电气耦合关系。δMIIFji越大,则换流母线之间的电气距离越近,换流母线j对换流母线i的参与度越强;反之,δMIIFji越小,则换流母线之间的电气距离越远,换流母线j对换流母线i的参与度越弱。
另外一种实用化的定义是根据阻抗矩阵元素来推导多馈入短路比[18]。假设在包含n回直流的多直流馈入系统中,各回直流注入系统的电流分别为I1、I2、…、In,则第j回直流对第i回直流的电压影响如式(2)所示。
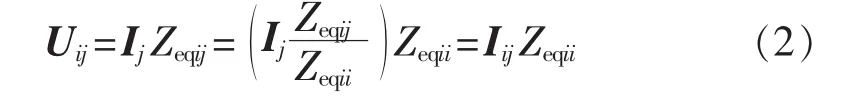
其中,Zeqij、Zeqii分别为从各直流换流母线看进去的等值阻抗矩阵Zeq的第i行第j列、第i行第i列元素;Iij为第j回直流对第i回直流换流母线注入电流的影响。
由式(2)可得第j回直流对第i回直流的功率影响为:
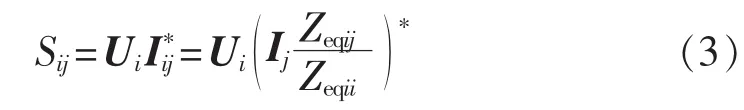
其中,Ui为第i回直流换流母线的电压。
采用类似直流潮流法所用的简化条件,即电力网络中各元件的电抗远大于电阻,δij数值很小,Ui≈Uj,其数值接近 1.0 p.u.,则式(3)可写为:
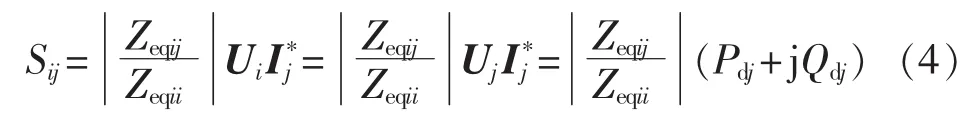
从而,第i回直流的等值直流功率为:
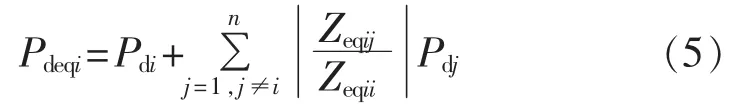
由上,多馈入短路比可表示为:
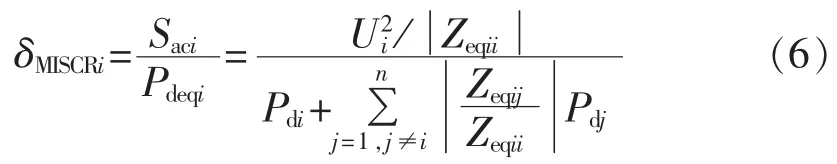
如果取换流母线额定电压为电压基值,则有:
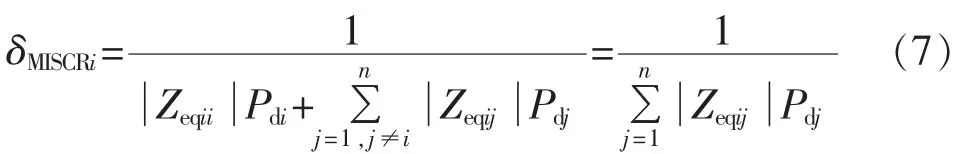
1.2 限制短路电流措施对多馈入短路比的影响
假设原网络有m个节点,并包含n回直流,m阶阻抗矩阵Zm的前n行n列为换流母线,当在该网络节点k与l之间追加阻抗为zkl的支路时,根据支路追加法和式(7)可以得到新的多馈入短路比如式(8)所示。
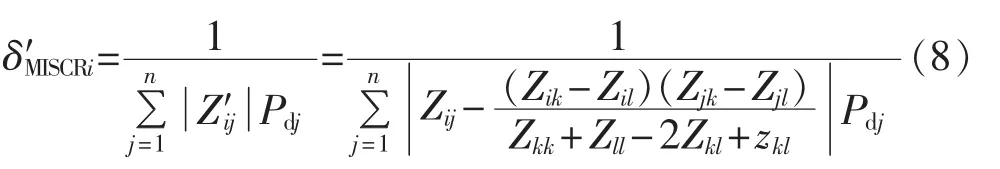
其中,i,j=1,2,…,n(n 为直流回数);k,l=1,2,…,m(m 为网络节点数);Z′ij为追加支路后阻抗矩阵 Z′m中第 i行第 j列元素;Zij、Zik、Zil、Zjk、Zjl、Zkk、Zll、Zkl分别为阻抗矩阵Zm中相应位置的元素。
多馈入短路比的变化量为:
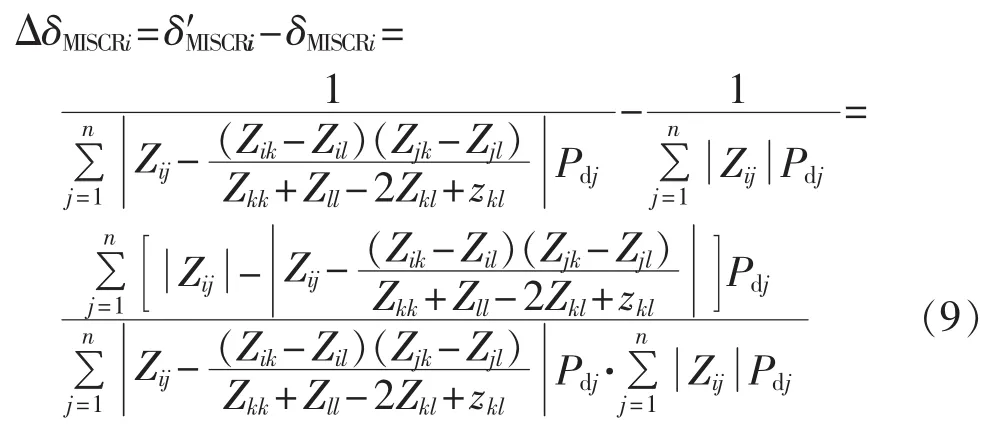
式(9)的分母部分大于0,假设网络阻抗矩阵元素均为纯感性电抗,则可将式(9)的分子部分改写为:

开断线路相当于在节点k与l之间追加阻抗为zkl=-z的支路,如图1所示[19]。由于线路电抗z通常远大于节点自阻抗,则有:

图1 开断线路等值模拟Fig.1 Equivalent model of opened line
加装限流电抗器相当于在节点k与l之间追加阻抗为 zkl=-(z2+zΔz)/Δz的支路,如图2所示[19]。同样有:


图2 加装限流电抗器等值模拟Fig.2 Equivalent model of line with current-limiting reactor
由Δ′表达式可以知道,其大小由电网结构以及元件参数决定,若 Δ′>0,则 ΔδMISCRi>0,若 Δ′<0,则ΔδMISCRi<0。限流措施一方面降低了换流母线短路容量,另一方面改变了各直流逆变站间的电气距离,从而可能使多馈入短路比增大,也可能使其减小。这就说明,存在既可以将短路电流控制在合理范围内,又能使多馈入短路比保持在较高水平的限流措施配置方案,需要通过建立多目标优化模型来求取。
2 限流方案多目标优化
2.1 数学模型
基于文献[19]的分析,限流方案优化的决策变量包括表示限流措施是否投入的控制变量us和表示限流设备的具体参数变量zs。
目标函数f1为限流措施的总投资成本:
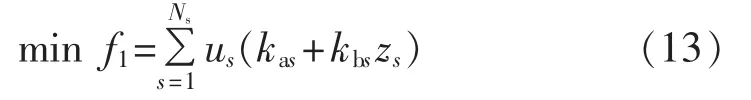
目标函数f2为系统中所有节点的短路容量裕度:

各变量含义可参见文献[19]。
短路容量能够反映系统各节点的抗扰动能力及网络关联强度[20],文献[19]考虑采用限流措施尽量不破坏网络联系的完整性和紧密性,因此取短路容量裕度最小为目标。同时,为兼顾限流效果,可根据工程经验指定短路电流控制上限。
目标函数f3衡量限流措施对多馈入短路比的影响,能够反映交流系统对多回直流的支撑能力,其值越大,表明交流系统的固有强度越强。具体定义为所有直流换流母线的加权多馈入短路比:

其中,δMISCRi为第i回直流的多馈入短路比;ωi为第i回直流的权重因子。
对式(6)进行变形,可得:
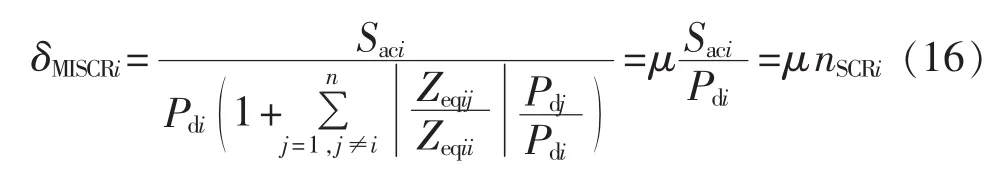
μ为计入多回直流相互影响之后,第i回直流短路比nSCRi的扰动系数。μ越小,多馈入短路比相对短路比的减小程度越大,其需要提高的必要性越大,则第i回直流在多直流馈入系统中的重要性越强。因此,ωi可有如下定义:

除上述目标函数外,限流方案优化需满足的约束条件包括系统没有孤立节点,潮流有功、无功平衡,短路电流、支路功率、节点电压、限流设备参数不越限[19]。在此基础上,本文增加一个约束条件,即多馈入短路比不低于最小值。具体如式(18)所示。

其中,δMISCRmin为多馈入短路比下限,其他变量含义可参见文献[19]。
此外,限流方案还要满足N-1静态安全约束,为简化问题求解,本文的处理方法是,在得到优选方案后对各种方案进行计算校核。
2.2 求解算法
多目标优化算法有3个主要的性能评价指标[21-22]:①所求得的解要尽量接近Pareto最优解;②要尽量保持解群体的分布性和多样性;③求解过程中要防止获得的Pareto最优解丢失。与此对应,NSGA-Ⅱ算法有3个关键技术使其成为一种优秀的多目标优化算法,即快速非支配排序、个体拥挤距离和精英策略,具体算法流程参见文献[23]。
开断线路和加装限流电抗器是目前比较实用的2种限流措施,因此,本文采用这2种典型限流措施进行优化。考虑在同一支路上可能存在不采用限流措施、开断线路或加装限流电抗器这3种状态,对种群中的N个个体进行整数编码,如图3所示。每个个体由M位组成,zl是个体的第l位的值,它可以是中的任意整数。 若 zl取 0,表示在支路l上不采用限流措施;若,表示将支路 l开断;若 zl取中的任意整数,表示在支路l上加装阻抗值为zl的限流电抗器。

图3 个体编码结构Fig.3 Code structure of individual
将式(18)的约束条件以罚值形式计入目标函数中,构造如下适应值函数:
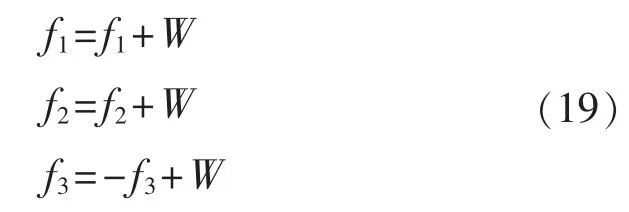
其中,W为罚值,若式(18)的所有约束条件均得到满足,则W=0,若存在某一约束条件未得到满足,则W为一充分大的正值。
综上,多目标优化方法流程如图4所示,支路筛选策略的详细计算流程参见文献[19]。其中,P0为t=0时的父代种群;ft、ft-30分别为第t代、第t-30代第1非支配层中所有个体的适应值的平均值;tmax为最大进化代数。
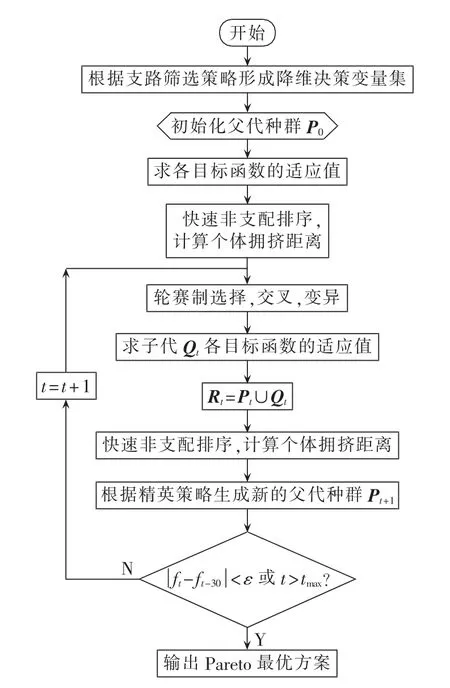
图4 多目标优化方法流程图Fig.4 Flowchart of multi-objective optimization
3 实际系统分析
编制了基于NSGA-Ⅱ算法的限流方案多目标优化程序,以上海电网实际系统为例,对本文方法的可行性和有效性进行验证。
考虑5%的裕度,对于最大遮断电流为50 kA的断路器,设定短路电流控制上限为47.50 kA;对于最大遮断电流为63 kA的断路器,设定短路电流控制上限为59.85 kA。设定限流电抗器的阻抗值范围为0~10 Ω;多馈入短路比最小值为 2.5[24];开断线路的成本系数为kas=60、kbs=0,加装限流电抗器的成本系数为 kas=625、kbs=25[25]。
根据规划,某年上海电网结构如图5所示。上海电网将有枫泾、南桥、华新、奉贤4个直流落点,形成典型的多直流馈入受端系统。该系统的多馈入短路比如表1所示。

图5 某年上海电网结构Fig.5 Structure of Shanghai Power Grid for a particular year
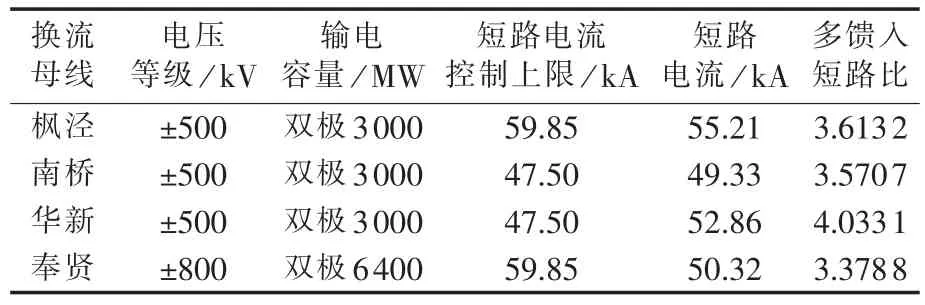
表1 上海电网多馈入短路比Table 1 Multi-infeed short circuit ratios of Shanghai Power Grid
华新站、南桥站500 kV母线的三相短路电流分别为52.86 kA和49.33 kA,均已超过断路器的短路电流控制上限(47.50 kA)。应用本文方法对上海电网进行限流方案多目标优化。根据支路筛选策略,对网络中的所有线路,按照综合限流措施灵敏度降序排列,如表2所示,选择灵敏度大于0.1的线路(低于 0.1的线路不具有竞争性)形成降维决策变量集。

表2 综合限流措施灵敏度排序Table 2 Branches sorted according to current-limiting measure sensitivity
设定种群规模为100,最大进化代数为100,交叉率为0.9。表3给出了综合400次仿真计算的统计规律,其中,个体维数在全维时为46,降维时为22,P为相应参数条件下每次计算求得的Pareto最优解与所有400次计算求得的Pareto最优解完全相符的概率的平均值。由表3可知,在仿真计算中采用降维决策变量,能够使算法具有较少的收敛代数和较好的收敛解;采用较大的变异率,虽然使算法的收敛代数增加,但是能够获得更接近Pareto最优解的收敛解。

表3 仿真计算统计特性比较Table 3 Comparison of statistic characteristic among simulative calculations
采用降维决策变量和较大的变异率进行仿真计算,某次优化在第30代时达到收敛。表4列出了部分具有代表性的Pareto最优方案,对应的目标函数适应值如表5所示。由该表可知,限流优化的总投资成本(f1)和短路容量裕度(f2)是互相矛盾的。以方案1和方案4为例,方案1对应的总投资成本最小,短路容量裕度最大;方案4对应的总投资成本最大,短路容量裕度最小。这2个目标函数互相矛盾是由限流措施的特性决定的,开断线路是限流效果最好、投资成本最低的限流措施,但是会明显降低网络联系的紧密程度;加装限流电抗器具有较开断线路更平滑的限流效果,能够在限流的同时尽量保持网络联系的紧密程度,但是其投资成本较大。

表4 Pareto最优方案Table 4 Optimal Pareto solutions

表5 Pareto最优方案适应值Table 5 Corresponding fitness values of optimal Pareto solutions
方案2对应的加权多馈入短路比(-f3)最大,并且较优化前的加权多馈入短路比(27.0877)也要大。仿真计算证明采用该限流方案后受端系统网架结构对多回直流的支撑能力得到加强,相同故障下系统电压和直流功率的恢复速度在所有方案中最快。各限流方案对应的多馈入短路比及短路电流水平如表6、表7所示。计算校核表明,以上限流方案均满足N-1静态安全约束。
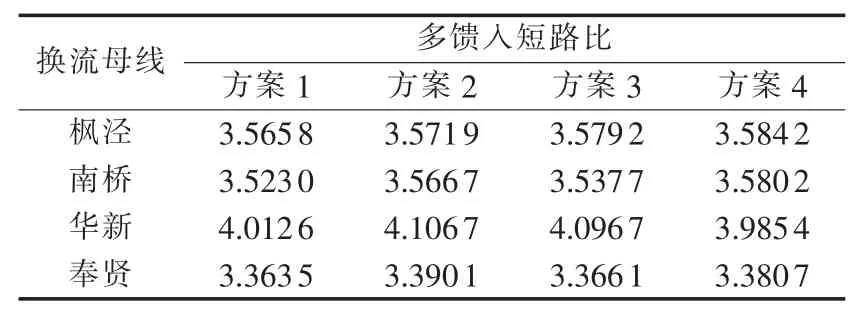
表6 各限流方案对应的多馈入短路比Table 6 Corresponding multi-infeed short circuit ratios of optimal Pareto solutions
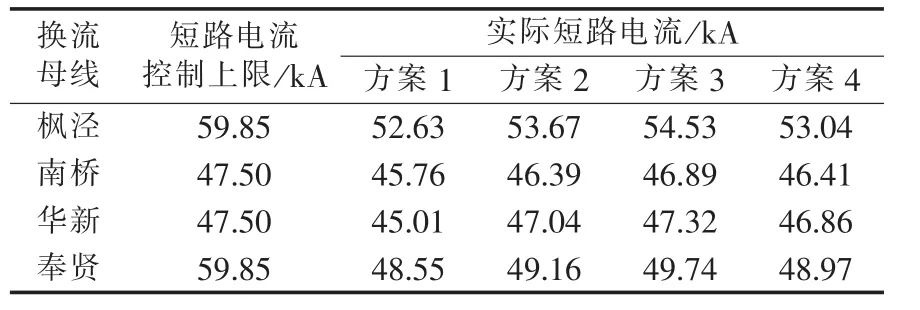
表7 各限流方案对应的短路电流水平Table 7 Corresponding short circuit currents of optimal Pareto solutions
与未考虑多馈入短路比的限流方案优化进行比较,若只考虑限流措施总投资成本最小,则优化结果为表4中的限流方案1;若只考虑保持网络联系的紧密程度,则优化结果为表4中的限流方案4。这就说明,采用本文方法不但可以提供限流措施总投资成本最小和网络联系紧密程度最强的限流方案,而且能够提供受端系统网架结构对多回直流支撑能力最强的限流方案,从而供决策者根据实际需求进行选择。
4 结论
为了协调解决短路电流超标和多回直流相互影响问题,本文提出了一种适用于多直流馈入系统的限流措施优化配置方法。上海电网实际系统仿真结果表明,应用NSGA-Ⅱ算法,结合支路筛选策略,在保证全局收敛性的前提下有效地提高了算法收敛速度;以总投资成本最小、短路容量裕度最小、加权多馈入短路比最大为目标,能够获得Pareto最优的限流方案集合,可以为决策者提供更丰富、更全面的选择空间。

