基于改进型迭代NR的磁感应断层成像图像重建算法
韩 敏 薛玉艳 秦 攀 韩 杰 姜长斌
1(大连理工大学电子信息与电气工程学部,辽宁 大连 116023)2(大连医科大学附属第一医院神经内科,辽宁 大连 116011)
基于改进型迭代NR的磁感应断层成像图像重建算法
韩 敏1*薛玉艳1秦 攀1韩 杰2姜长斌2
1(大连理工大学电子信息与电气工程学部,辽宁 大连 116023)2(大连医科大学附属第一医院神经内科,辽宁 大连 116011)
在磁感应断层成像中,图像重建是一个典型的病态问题,其数值解存在不稳定性。针对此问题,提出一种基于加权矩阵和L1范数正则化的改进型迭代Newton-Raphson (NR)算法。该算法通过在目标函数的误差项中引入加权矩阵,同时在L2范数正则化惩罚项的基础上引入L1范数正则化,改善图像重建解的病态性。 设置3种典型的模型,分别对有无噪声的数据进行分析,将本算法与Tikhonov正则化算法和迭代NR算法进行对比。在无噪声数据分析中,所提算法相对Tikhonov正则化算法和迭代NR算法的相对图像误差减小0.11~0.14,相关系数提高13%~17%。在有噪声数据中,所提算法相对于Tikhonov正则化算法和迭代NR算法的相对图像误差减小0.06~0.09,相关系数提高7%~10%。提出的算法成像性能较好,且抗噪性能较强,为进一步的实验重建精确性提供理论依据。
磁感应断层成像;图像重建;L1范数正则化;迭代Newton-Raphson
引言
磁感应断层成像(magnetic induction tomography,MIT)是一种基于电磁检测原理测量生物组织电导率分布的成像技术,具有非接触、可以进行实时图像监护等优点,在生物医学成像中具有潜在的应用价值[1-2]。MIT的最终实现是基于图像重建算法,可将检测系统测量的电压信号转化为与生物组织电导率分布相关的图像[3]。图像重建算法是一个非线性的病态问题,输入数据的微小变化都会引起解的较大变化,其解存在严重的不稳定性。同时,由于生物组织电导率之间的差异较小,所以图像重建变得更加困难,重建后图像的分辨率较低[4]。图像重建算法是MIT技术进一步发展的主要难点,因此探索具有较高成像精度的重建算法具有重要的意义。
目前,MIT技术中改善图像重建病态性问题通常采用正则化算法[5],用于保证求解的适定性。图像重建的方法主要有线性反投影算法[6]、Landweber迭代算法[7]、Tikhonov正则化算法[8]、迭代Newton-Raphson(NR)算法[9]。其中,线性反投影算法简单、重建速度较快,然而仅适用于电导率对比度高的成像中,其重建结果容易出现星状伪迹,定位比较困难。Landweber迭代算法采用迭代的形式进行重建,但是耗时较长。Tikhonov正则化算法是在其目标函数中加入L2范数惩罚项,惩罚极端电导率的变化,可以保证解的稳定性,然而重建后会产生人工平滑效果,致使目标与背景区域之间的边界模糊,容易降低成像的分辨率。迭代NR算法是一种基于最小二乘理论的方法,通过寻找最优的电导率分布,提高图像的分辨率,定位较精确,但当测量数据存在较小的变化时,将会对重建后的电导率造成较大的影响,算法的稳定性较差。采用上述方法进行成像,重建图像的分辨率较低,成像误差较大。
针对上述问题,为了提高数值解的稳定性,笔者提出一种基于加权矩阵和L1范数正则化的改进型迭代NR算法,减小估计误差,提高图像重建的精度和算法的抗噪性能。这种方法的基本思想是:为减小测量数据和仿真数据之间的误差,在目标函数的误差项中引入加权矩阵;同时,为了保证图像重建后电导率值的真实性,有效保护边缘电导率信息,在目标函数的惩罚项中加入L1范数正则化。通过仿真实验,与Tikhonov正则化算法、迭代NR算法比较,验证所提出算法的有效性。
1 MIT技术图像重建
MIT技术是根据被测场域中的测量电压,重建场域内部电导率的空间分布。在被测场域边界施加正弦交变电流,当被测场域内电导率分布变化时,会导致场内电势分布变化,从而使得场域边界上的测量电压发生变化;通过一定的图像重建算法,可重建出被测场域中的电导率分布[10]。其中,在已知初始电导率分布的情况下,求解检测线圈的电压数据和灵敏度矩阵,即为前向问题的求解[11-12]。前向问题的求解为测量系统的设计提供理论指导,更为图像重建过程提供测量数据。基于此测量数据,采用优化算法进行图像重建,不断更新电导率的分布,使前向问题求解计算电压数据与测量电压数据的误差最小,从而得到最优的电导率值,实现电导率重建。
1.1图像重建理论
MIT的图像重建过程[13]是在已知各个检测线圈感应电压的情况下,研究被测区域的电导率分布情况,实现其电导率分布的可视化。对于MIT图像重建来说,测量电压和图像分布之间的关系为
V=F(σ)
(1)
式中,V∈M为测量电压,M为独立测量个数;F∈N×N是前向求解算子,表示电导率与电压数据之间的对应关系,N为有限元剖分单元的个数;σ∈N为电导率分布。
MIT的图像重建过程常常近似为线性问题,线性化的提出可以有效地将复杂问题进行简化,然而线性近似过程对电导率变化较大的情况处理效果不好,所以重建的求解过程需要采用迭代的形式。同时,由于MIT本身问题是病态的,所以通常对该问题进行正则化处理。
MIT的图像重建问题线性化可近似描述为
F(σ) -Vm=S(σ-σt)+O(‖σ-σt‖2)
(2)
式中,Vm∈M是测量电压数据,M为独立的测量数;σt∈N为已知电导率分布,N为有限元剖分网格的单元数;σ∈N为电导率分布;S∈M×N为灵敏度矩阵,表示被测区域电导率的微小变化对检测线圈电压的影响;O(·)表示无穷小。
在MIT实际测量系统中,由于检测线圈的个数有限,检测电压的个数小于未知电导率的个数,致使解的不唯一,其求解过程为病态性,即测量数据的微小变化会引起解向量较大的扰动[14]。采用最小二乘法进行求解,同时为了降低解的不稳定性,在图像重建的目标函数中引入正则化,可以有效解决病态性的问题。
1.2Tikhonov正则化算法
Tikhonov正则化算法[15]的思想是最小化目标函数,有
(3)
式中,前一项为误差项,后一项为惩罚项;Vm为测量的电压值,F(σ)为前向计算的电压,σ为电导率分布;ασr≥0是正则化参数,用于控制惩罚项的大小,衡量数据项和正则化项之间的相对贡献量。
正则化项的加入可以有效平衡问题的偏差和方差,即通过引入小的偏差(即惩罚项),可以使求解问题的方差大幅降低,提高数据解的稳定性。R为正则化矩阵,定义为一阶拉普拉斯算子,其形式为
(4)
最后,可得电导率为
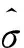
(5)
由于Tikhonov正则化算法是采用L2范数的函数为正则化函数,对重建后的图像起到平滑作用,使图像的空间分辨能力较低。
2 改进型迭代NR图像重建算法
为了减小估计误差,提高求解精度,本研究对迭代NR算法尝试进一步改进。通过在其目标函数中引入加权矩阵,以求提高求解精度;同时,为了保护图像的边界信息,增强图像的保真性,在其惩罚项中加入L1范数正则化项。
2.1目标函数的建立
以电压测量值和计算值的误差范数平方作为目标函数,最小化目标函数为
(6)
可以采用最小二乘的方法求解式(6)。在最小二乘估计中,认为各测量值之间具有相同的测量误差;而在实际MIT技术中,因设备不同或者测量环境不同,各测量值可能不具备这一条件,因此最小二乘方法不能得到最优的估计值。为了提高估计精度,降低估计误差,在最小二乘的基础上引入加权矩阵,构成一种加权最小二乘形式[16],最小化目标函数为
(7)
式中,W为加权矩阵。
在目标函数中引入加权矩阵,通过权值可以使估计误差变小,抑制重建迭代过程中误差累积的影响,改善求解的精度。为保证求解是无偏估计或最小方差无偏估计,加权矩阵要求为对称正定矩阵。利用许瓦兹不等式可以证明[17],当加权矩阵W=(E(NNT))-1时,求解的估计均方误差最小,其中N为独立分布的高斯随机噪声。
采用无约束的最优化方法求解式(7),但结果通常并不唯一或者说是不稳定的。为了获得稳定解,通常要对目标函数附加某些约束条件,这种解决不适定问题的有效方法是正则化处理。在式(7)基础上加入正则化项,用于降低解的不稳定性,有效解决不适定问题,即在目标函数中加入惩罚项,得到最小化目标函数为
(8)
式中,前一项为误差项,后一项为惩罚项;ασr≥0是正则化参数,控制惩罚项的大小,衡量数据项和正则化项之间的相对贡献量;σ为电导率分布。
式(8)中引入的正则化是L2范数的形式,对式(8)求解进行图像重建时,图像的边缘及细节产生过度的平滑,从而导致重建图像边缘模糊。对此,则考虑额外的平滑和稀疏惩罚,在加权最小二乘的基础上,引入L1范数正则化[18],可以对重建图像的保真度进行约束,保护图像的边缘信息,其改进的目标函数为
(9)

若正则化系数ασs=0,加权矩阵W为单位阵时,该算法即为迭代NR算法。
2.2求解过程
对式(9)进行求解,在初始电导率σ0处进行泰勒级数展开,即
(10)


(11)
所以
(12)
其中,函数g的梯度为
(13)
函数g的Hessian矩阵为
(14)
Hessian矩阵近似为式(14)中等号右端的第2项形式,将式(13)与式(14)代入式(12),整理得电导率修正公式,即
(15)
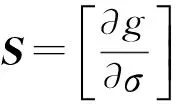
最终得到的迭代公式为
(16)
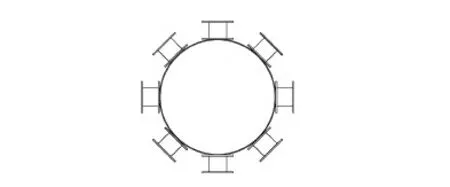
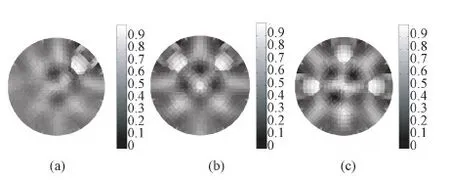
为了保证图像重建问题的线性,通常使用初始的灵敏度矩阵作为每步迭代的灵敏度矩阵,即在每步更新中灵敏度矩阵保持不变。同时,为了避免出现局部最小的情况,定义一个步长参数l(0 (17) 2.3算法实现步骤 基于加权矩阵和L1范数正则化的改进型,迭代NR算法的实现主要包括6个步骤。 步骤1:采用有限元法求解前向问题,得到电压数据,根据式(1),将前向计算的电压值作为测量数据。 步骤2:初始化迭代次数n0,利用σ0=(STS+ασrRTR)-1ST(F(σ)-Vm),其中正则化参数ασr设为较小的数;基于最小二乘理论,确定电导率的初始值σ0。 2.4仿真实验与算法评价 为验证算法的有效性,先采用有限元法计算前向问题,将前向计算的电压数据作为测量数据。仿真实验采用所提出的改进型迭代NR算法进行图像重建,并与Tikhonov正则化算法和迭代NR算法进行比较,在相同尺度下,验证本算法的有效性。 为获取MIT系统用于产生图像重建所需要的数据,在仿真系统中采用8个线圈的形式,分别用来作为激励线圈和检测线圈。线圈的内径为0.022 m,外径0.03 m,长度为0.04 m,其绕制方式是在其内径上沿线圈轴线方向单方向缠绕30匝。8个线圈均匀分布在圆周上,两个相对位置线圈的距离为0.240 m,以圆周的中心作为坐标轴原点。图1所示为仿真MIT系统的线圈排列,8个线圈中,1个线圈作为激励线圈,其他线圈作为检测线圈,依次循环。在激励线圈中,通以电流密度为1 A/m2、激励频率为10 MHz的正弦交变电流,求取检测线圈上的电压数据作为图像重建的原始数据。 图1 激励-检测线圈排列Fig.1 The arrangement of excitation-detection coil 采用有限元法进行网格划分。图2 (a)所示为细网格划分,将研究区域剖分为1 152个三角元网格,625个节点,作为前向问题的计算,用于保证计算精度。图2 (b)为粗网格划分,将研究区域剖分为288个三角元网格,169个节点,用于图像重建问题的分析,降低问题的病态性。为了模拟MIT在测量生物组织的能力,采用3%(σ=2.31 S m-1)的NaCl溶液作为目标扰动区域,0.9%(σ=1.58 S m-1)的生理盐水作为背景区域,利用上述仿真条件进行数据的获取与分析。 图2 网格划分。(a) 细网格划分;(b) 粗网格划分Fig.2 Meshing map.(a) Fine mesh map; (b) Coarse mesh map 设置3种典型的分布用于仿真试验,其中白色区域表示扰动目标区域,即表示病变的位置和大小,黑色区域表示背景区域。在图3中,(a)表示扰动个数为1个的初始电导率分布模型,(b) 是扰动个数为2个不同位置的初始电导率分布模型,(c)是扰动个数为3个不同位置的初始电导率分布模型。 图3 仿真实验模型。(a) 1个扰动;(b)2个扰动;(c)3个扰动Fig.3 Simulation model.(a) One disturbance; (b) Two disturbances; (c) Three disturbances 为了更直观地评价重建图像的质量,在仿真实验中,分别采用重建图像的相对图像误差εe和相关系数εr两性能指标,评价图像重建算法的有效性。 相对图像误差反映重建后图像的电导率相对于初始电导率分布的偏离程度,值大于或等于零,值越小表明重建的精度越高。相对图像误差为 相关系数用来衡量重建图像与原始图像之间的相关程度,值越大表明重建的效果较好,可定义为 将本算法与Tikhonov正则化算法和迭代NR算法进行对比分析,验证所提算法的有效性。 图4(a)~(c)所示为采用Tikhonov正则化算法进行成像的结果,图5(a)~(c)为迭代NR算法成像的结果,图6(a)~(c)为本算法成像的结果。由于在电导率重建过程中,得到的是电导率的相对变化量,不能重建出实际电导率的大小[19]。在仿真中,将电导率的相对大小映射到有限元单元中,为了更加公平地对比分析不同算法的成像效果,将3种算法重建后的电导率进行归一化处理。 图4 Tikhonov正则化算法成像结果。(a) 1个扰动;(b)2个扰动;(c)3个扰动Fig.4 The imaging results with Tikhonov regularization algorithm.(a) Imaging of one disturbance; (b) Imaging of two disturbances; (c) Imaging of three disturbances 图5 迭代NR算法成像结果。(a) 1个扰动;(b)2个扰动;(c)3个扰动Fig.5 The imaging results with iterative NR algorithm.(a) Imaging of one disturbance; (b) Imaging of two disturbances; (c) Imaging of three disturbances 图6 本算法成像结果。(a) 1个扰动;(b)2个扰动;(c)3个扰动Fig.6 The imaging results with this article algorithm.(a) Imaging of one disturbance; (b) Imaging of two disturbances; (c) Imaging of three disturbances 从图4~6中可以看出,对3种典型的仿真模型进行成像时,所提方法所得到的重建图像能够较好地确定目标导体的位置、形状,且目标导体与背景区域的边界较清晰,伪影较少,图像分辨能力强。而Tikhonov正则化算法和迭代NR算法得到的重建目标导体与背景区域的边界模糊,干扰严重,重建效果较差。 比较3种方法的相对图像误差εe和相关系数εr,其结果如表1所示。 表1 图像重建算法性能的评价指标Tab.1 Performance evaluation of image reconstruc-tion algorithm 从表1可以看出,当仿真模型中的扰动只有1个时,本方法的相对图像误差εe=0.749 2,对比Tikhonov正则化算法的εe=0.958 0和迭代NR算法的εe=0.921 1要小,说明本方法重建图像的值更接近初始电导率分布。同时,本方法的相关系数εr=74.28%,相比Tikhonov正则化算法的εr=48.83%和迭代NR算法的εr=49.26%要大,说明重建图像与原始图像的相关程度较大,且重建图像的分辨率较高。当仿真模型中扰动的个数为2和3时,同样本方法的相对图像误差最小,且本文所提方法的相关系数较Tikhonov正则化算法和迭代NR算法要大,说明本方法重建得到的图像更接近于仿真模型中的初始电导率分布情况。 为了验证所提出算法的抗噪性能,选择图3中的(a)模型为仿真实例。在有限元计算得到的前向问题的电压数据中,加入信噪比(SNR)分别为20、40、60、70 dB的高斯噪声,测试不同方法在模型参数等价、正则化参数一定且最优情况下的仿真结果。图7~10所示分别为信噪比为20、40、60、70 dB时基于上述3种方法得到的重建结果。 图7 SNR=20 dB时的成像结果。(a)Tikhonov正则化算法;(b)迭代NR算法;(c)本算法Fig.7 The imaging results with SNR is 20 dB.(a) The imaging of Tikhonov regularization; (b) The imaging of iterative NR; (c) The imaging of this article 图8 SNR=40 dB时的成像结果。(a)Tikhonov正则化算法;(b)迭代NR算法;(c)本算法Fig.8 The imaging results with SNR is 40dB.(a) The imaging of Tikhonov regularization; (b) The imaging of iterative NR; (c) The imaging of this article 图9 SNR=60 dB时的成像结果。(a)Tikhonov正则化算法;(b)迭代NR算法;(c)本算法Fig.9 The imaging results with SNR is 60dB.(a) The imaging of Tikhonov regularization; (b) The imaging of iterative NR; (c) The imaging of this article 图10 SNR=70 dB时的成像结果。(a)Tikhonov正则化算法;(b)迭代NR算法;(c)本算法Fig.10 The imaging results with SNR is 70 dB.(a) The imaging of Tikhonov regularization; (b) The imaging of iterative NR; (c) The imaging of this article 从重建结果可知,对前向问题求解的电压数据加入不同信噪比的噪声进行仿真分析时,在不同的信噪比下,所提方法仍能较好地进行重建,重建图像能够较好地确定目标导体形状,算法抗噪性能较强。Tikhonov正则化算法在不同信噪比下的成像结果有较大的差异,成像结果伪迹严重,算法的抗噪性能较差。迭代NR算法成像的边缘较模糊,加入不同信噪比的噪声后,算法的抗噪性能较差,成像效果欠佳。对比分析图7~10可知,加入不同信噪比的高斯白噪声进行仿真实验,在相同的仿真条件下,本算法重建得到的图像效果较好,说明其抗噪性能较强。 为了更直观地评价算法的抗噪性能,对比不同信噪比加噪声后3种方法的相对图像误差εe和相关系数εr,其结果如表2所示。 表2 不同信噪比下图像重建算法性能的评价指标Tab.2 Performance evaluation of image reconstruction algorithm with different SNR 从表2可以看出,在有限元前向计算电压仿真数据中加入不同SNR的高斯白噪声,在相同仿真条件下,与其他两种方法相比,本方法的相对图像误差最小,且所得到的相关系数最大,进一步说明本方法成像质量较好,具有较强的抗噪性能。 磁感应断层成像中,由于逆问题存在病态性,其数值解不稳定,重建图像的分辨率较低,成像质量较差。笔者对迭代NR算法进行改进,对比图4~6可知,在不同的扰动数目下进行仿真,本方法得到的成像效果较Tikhonov正则化算法和传统迭代NR算法的成像质量好,成像的分辨率高,成像中的干扰较少,能有效地将目标导体与背景区域区分开。同样,由表1中的成像质量评价指标可知,本方法的相对图像误差最小,相关系数最大,进一步说明与MIT中的常用方法相比,本方法得到的重建图像质量有了一定的提高,有效减弱了问题的病态性。由图3所示的仿真实验模型可以看出,本仿真采用的模型是形状不规则的扰动目标作为病变组织的模拟,更能有效模拟实际的病变情况,使得仿真分析更具有说服力。 进一步以一个扰动目标为实例,将有限元前向计算电压数据中加入不同信噪比的高斯白噪声。在相同的仿真条件下,对比分析不同SNR下Tikhonov正则化算法、迭代NR算法和本算法的成像效果。对比图7~10的成像结果可知,在不同SNR下,本算法的成像效果最好,说明本算法的抗噪性能较好。同样,由表2中的评价指标同样可以看出,在不同的SNR下,本方法的性能指标更优。 因此,本研究基于迭代NR算法,通过在目标函数中引入加权矩阵,以及在惩罚项的基础上引入L1范数正则化的改进迭代NR算法研究,与之前的方法相比,具有一定的优势,但在成像后发现重建图像的分辨率有待加强,病态性问题还有待完善。 本研究提出一种基于加权矩阵和L1范数正则化的改进型迭代NR算法,有效改善了图像重建中的病态性问题,提高了求解的数值稳定性。在迭代NR算法的基础上,改进目标函数,减小估计误差,提高求解精度;同时引入L1范数正则化,对图像重建保真度进行约束,保护边缘信息,降低解的不稳定性。设置3种典型的分布用于仿真实验,证明了本方法的有效性;与其他方法相比,本方法可以很好地确定目标导体的位置和形状,重建图像的分辨能力强,且重建后图像的相对误差较小,相关系数较大,算法的稳定性较好,抗噪性能较强。 [1] Griffiths H.Magnetic induction tomography [J].Measurement Science and Technology,2001,12(8):1126-1131. [2] Mamatjan Y.Imaging of hemorrhagic stroke in magnetic induction tomography:Aninvitrostudy [J].International Journal of Imaging Systems and Technology,2014,24(2):161-166. [3] Merwa R,Hollaus K,Brunner P,etal.Solution of the inverse problem of magnetic induction tomography (MIT)[J].Physiological Measurement,2005,26(2):241-249. [4] Teniou S,Meribout M,Al-Wahedi K,etal.A Near-infrared-based magnetic induction tomography solution to improve the image reconstruction accuracy in opaque environments [J].IEEE Transactions on Magnetics,2013,49(4):1361-1366. [5] Jin B,Khan T,Maass P.A reconstruction algorithm for electrical impedance tomography based on sparsely regularization [J].International Journal for Numerical Methods in Engineering,2012,89(3):337-353. [6] 刘俐,李倩,何为,等.一种均匀激励磁场磁感应成像的改进反投影算法[J].中国生物医学工程学报,2014,3(33):313-319. [7] 王兵贤,胡康秀,王泽文.反问题的Landweber迭代法及其应用研究进展[J].计算机应用研究,2013,9(30):2583-2586. [8] 陈玉艳,王旭,吕轶,等.基于 Tikhonov 和变差正则化的磁感应断层成像重建算法[J].东北大学学报(自然科学版),2011,32(4):460-463. [9] Hsin YW,Soleimani M.Hardware and software design for a National Instrument-based magnetic induction tomography system for prospective biomedical applications [J].Physiol Measurement,2012,33(5) :863-879. [10] 吕轶,王旭,金晶晶,等.正则化一步动态重建算法在磁感应成像中的应用[J].电子学报,2011,39(12):2801-2806. [11] 柯丽,庞佩佩,杜强.基于伽辽金有限元法的磁感应断层成像正问题仿真[J].中国生物医学工程学报,2012,1(31):53-58. [12] Bras NB,Martins RC,Serra AC,etal.A fast forward problem solver for the reconstruction of biological maps in magnetic induction tomography [J].IEEE Transactions on Magnetics,2010,46(5):1193-1202. [13] Zhang M,Ma L,Soleimani M.Magnetic induction tomography guided electrical capacitance tomography imaging with grounded conductors[J].Measurement,2014,53(7):171-181. [14] Chen Yinan,Yan Ming,Chen Dayu,etal.Imaging hemorrhagic stroke with magnetic induction tomography:Realistic simulation and evaluation [J].Physiological Measurement,2010,31(6):809-816. [15] Wang Linjun,Xie Youxiang.Application of tikhonov regularisation method in bounded chord subjected to enforcement [J].International Journal of Service and Computing Oriented Manufacturing,2013,1(2):141-153. [16] 基均; 刘进; 蔡强.基于全变差的加权最小二乘法PET图像重建[J].电子学报,2013,4(4):787-790. [17] 王建刚,王福豹,段渭军.加权最小二乘估计在无线传感器网络定位中的应用[J].计算机应用研究,2006,23(9):41-43. [18] Andrzej C,Rafal Z,Anh HP,etal.Nonnegative Matrix and Tensor Factorizations:Applications to Exploratory Multi-way Data Analysis and Blind Source Separation [M].Tokyo:A John and Sons Ltd,2009:203-220. [19] Soleimani M.Image and shape reconstruction methods in magnetic induction and electrical impedance tomography [D].England:University of Manchester,2005. AnImprovedImageReconstructionAlgorithmBasedonIterationNRinMagneticInductionTomography Han Min1*Xue Yuyan1Qin Pan1Han Jie2Jiang Changbin2 1(FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian116023,Liaoning,China)2(DepartmentofNeurology,FirstAffiliatedHospitalofDalianMedicalUniversity,Dalian116011,Liaoning,China) The image reconstruction process is a typical ill-posed problem in magnetic induction tomography (MIT),in which the numerical solution is unstable.To solve this problem,an improved iteration Newton-Raphson algorithm based on weighted matrix and L1-norm regularization is improved.The proposed method adds the weight matrix in the objective function and adds L1-norm regularization term in L2-norm regularization penalty term.The analysis is made for three typical models in the data with and without noise,respectively.And the proposed algorithm is contrasted with Tikhonov regularization algorithm and iterative NR algorithm.In the data without noise,relative to Tikhonov regularization algorithm and iterative NR algorithm,the relative error is reduced by 0.11-0.14.And then,the correlation coefficient is raised by 13%-17%.The algorithm has good performance in imaging.In the data with noise,the relative error is reduced by 0.06-0.09,and the correlation coefficient is raised by 7%-10% in the proposed algorithm.The algorithm has good anti-noise performance,which has offered theory basis for the study of reconstruction accuracy. magnetic induction tomography (MIT); image reconstruction; L1-norm regularization; iteration Newton-Raphson 10.3969/j.issn.0258-8021.2015.02.009 2014-08-20,录用日期:2015-02-05 中央高校基本科研业务费专项项目(DUT13JB08);大连市科技局科技计划项目(2012C014) R318 A 0258-8021(2015) 02-0190-08 *通信作者(Corresponding author),E-mail:minhan@dlut.edu.cn




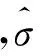

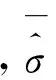
3 结果







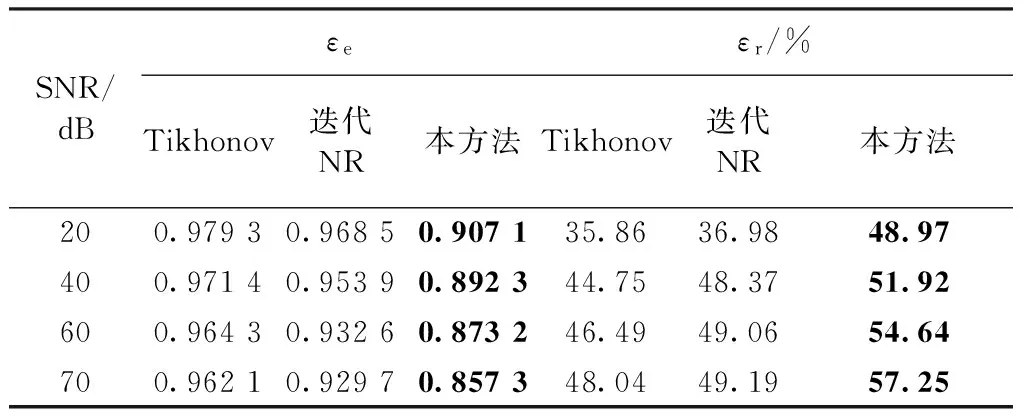
4 讨论
5 结论

