基于Contourlet域高阶统计量的图像隐写分析

王昌盛，张大伟，陈智博

(军械工程学院信息管理中心，石家庄 050003)

隐写术作为信息隐藏的一个重要分支，用于保护隐藏在载体中信息的安全性。针对隐写术的攻击称为隐写分析，它是在已知或未知嵌入算法的情况下，通过统计分析或模式分类等手段检测观测对象中是否存在秘密信息的技术。由于在保障信息安全和提高隐写算法安全性等方面具有重要的指导意义，隐写分析已成为信息隐藏领域研究的热点。

由于小波分解在信号处理和图像处理中的广泛应用，基于小波高阶统计量的隐写分析也引起了国内外许多学者的关注，成为了一种重要的隐写分析方法。如Hary Farid提出了一种基于高阶统计量的检测模型［1］，取得了很好的效果。但是Farid的方法也存在一些问题。

首先，小波并不是表示图像的最优基。因为在二维图像中，由于边缘、轮廓和纹理等具有高维奇异性的几何特征包含了大部分信息，秘密信息也多嵌入在这些位置。而二维小波是由两个一维小波的张量积形成，本质上仍然是一维变换，其基函数只有水平、垂直、对角线3个方向，它难以表示具有线奇异和曲线奇异等更高维的几何特征。针对上述缺点，需要发展新的高维函数的最优表示方法。Do等［2］提出了一种“真正的”二维图像的表示方法，即Contourlet变换。Contourlet基的支撑区间是随尺度而变化的“长条形”结构，因而具有比小波变换更好的多分辨率、局部性、方向性和各向异性，能更加有效地捕获图像的边缘信息。

其次，Farid采用了一个线性预测模型，通过某小波系数“附近”的系数进行线性组合作为该系数的预测值并计算预测误差，把这个预测误差的统计特征作为第二组特征向量。但是这个线性模型的参数只能通过经验获得，如果参数选择不当，对隐写分析算法的性能影响非常大。

我们知道，隐写分析要解决的一个重要问题就是提取合适的统计特征，而统计特征的获得却依赖于自然图像的统计模型。在隐写分析研究的初期，为了简化问题，一般都假设图像的采样(如像素、DCT系数、DWT系数等)间是独立同分布的，忽略了采样间的统计相关性。但是随着研究的深入，人们发现，图像采样间实际上是统计相关的，独立同分布的假设会低估隐写分析算法的性能，高估隐写算法的安全性［3］。因此人们逐渐将各种相关性模型引入隐写分析中，以期得到更好的性能。例如，Sullivan［3］使用描述像素间相关性的MC(马尔科夫链)模型用于扩频类和量化索引类隐写算法的检测。Farid的线性模型也考虑了小波系数之间的相互关系，但并没有完整精确地刻画出小波系数间的相关性，还有改进的空间。

基于以上分析，将Contourlet变换引入隐写分析，并采用相关性模型来提取特征，这是一个很好的研究思路。相关的研究有文献［4，5］，但是前者对同样采用了Farid的线性相关模型，后者使用了互信息，两者都不能完全刻画Contourlet系数不同尺度和方向的相关性。本文采用Contourlet域隐马尔科夫树(CDHMT)模型来描述Contourlet系数的相关性。实验结果表明，本文提出的方法是一种更加有效的隐写分析方法。

1 特征提取

Farid提取的小波高阶统计特征分为两个部分，一部分是图像小波分解后各个尺度在水平、垂直和对角三个方向的均值、方差、斜度和峭度，第二个统计特征子集是基于系数量值的最佳线性预测器所产生的对数误差值，在各个尺度、子带上计算上述4个统计特征而形成的，两个特征子集共计24(N-1)维特征(N为小波分解的尺度)。受她的启发，我们在Contourlet域也将提取类似的统计特征，第一个特征子集是图像Contourlet分解后各个尺度、各个方向子带的均值、方差、斜度和峭度，第二个特征子集是采用基于CDHMT模型的预测误差值，再同样计算上述4个统计量而得到的。在此基础上对特征值进行加权处理，形成最终的特征集。

1.1 预测误差的计算

Farid采用的线性预测器来形成预测值。这种方法有两个缺陷:一是没有完全揭示出系数之间的相关性，二是邻近小波系数的权重不好确定，主要依靠经验，如果权重确定的不当，对分类结果影响很大。在此采用CDHMT模型来形成预测值。

在图像隐写分析中，一般都假设嵌入的秘密信息是高斯白噪声，即隐写过程可以表示为

u、v和e分别指载体图像、隐写后的图像和嵌入图像的Contourlet系数，问题就转化为已知 v，尽可能准确地估计出u。

由隐写图像，可以计算出相应的CDHMT模型参数θv，减去噪声的方差，可以得到估计图像的模型参数θu。如下式:

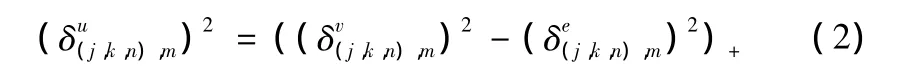
这里(j，k，n)是指 Contourlet分解中尺度 j、方向 k 的子带中第n个系数，m是该系数的状态。可以用蒙特卡洛方法估计出来。(y)+的定义是

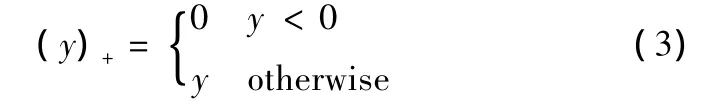
如果给定状态 Sj，k，n=m，Contourlet系数服从零均值的高斯分布，那么问题就简化为从零均值高斯噪声中估计出一个零均值高斯信号。这个问题已经有现成的解法［6］

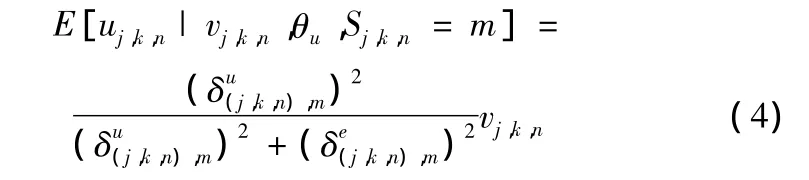
而在使用EM算法进行CDHMT模型训练的时候，已经可以计算出 p(Sj，k，n=m|vj，k，n，θu)，因此得到以下式子

预测误差就可以通过公式得到

分别在各个尺度和方向的子带中计算均值、方差、斜度和峭度就可以得到第二个特征子集。因此，在尺度j，方向k的子带上得到的特征集合是

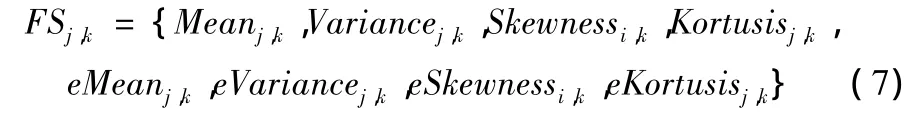
1.2 特征加权

为了增强特征的鲁棒性，我们对上述提取的两组特征进行加权处理，权重的依据是各子带的标准差的大小。Contourlet变换各子带的标准差反映了各子带灰度相对于灰度均值的离散情况，标准差越大，则灰度级分布越分散，高频分量越高，应该赋予其较大的权值;反之，则赋予其较小的权值。通过加权使得不同子带信息的重要性反映到最终的特征量中。

设尺度为j、方向为k的子带的权重为wj，k，定义为

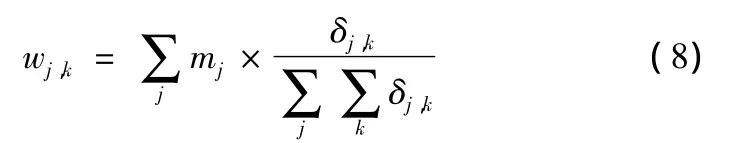
这里需要用到各个子带的标准差，这个值不需要重新计算，因为在求解CDHMT模型参数的时候就已经计算出来了，计算权重的时候可以直接使用。那么，经过加权处理后形成的最终特征集合就是

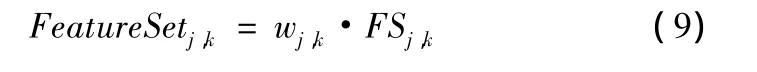
1.3 特征归一化

为了消除各特征之间量纲、量级等不同的影响，消除量度偏差，且使各个特征数据具有可比性，在分析之前需要对原始特征数据进行归一化处理。本文的归一化采用高斯归一化方法［7］，其特点是少量超大或超小的元素值对整个归一化后的元素值分布影响不大。

2 分类器SVM

SVM(支持向量机)在解决小样本、非线性样本以及高维机器学习问题中表现出许多特有的优势，此外，许多学者的研究成果都表明，SVM的分类效果“似乎”优于其他传统分类工具。因此，本文同样采用SVM作为通用隐写分析的分类器。

3 实验结果

实验所用的原始图像是从NRCS图像数据库中随机选取的2500幅彩色JPEG图像。将选取的图像从中央截取512×512大小的一块，并转化为灰度图像后，作为实验用图像。将得到的灰度图像随机平均分为5组，每组500幅，第1组不嵌入任何数据，第2组到第5组图像分别使用时空域的± LSB［8］、DCT 域的 F5［9］、DWT 域的 CDMAICA［10］等 4 种隐写算法嵌入秘密信息，每组图像都随机选取400幅用于训练，剩余的100幅用于测试。实验的时候，使用第1组分别和其他4组进行组合，测试对这4种嵌入算法的识别性能。按照嵌入强度的不同重复做上述实验，嵌入强度分别为0.01、0.05、0.1 和 0.15，单位是 bpp(bit per pixel)。

特征提取时使用Contourlet Hidden Markov Tree toolbox工具箱，对每幅图像进行3层分解，每层分别有4、8和8个方向子带。这样每幅图像提取8×(4+8+8)=160维的特征。SVM采用OSU SVM Toolbox工具箱，采用RBF核，默认参数。定义识别率为正确识别的图像数目与总测试图像数目的百分比，实验结果如表1所示。

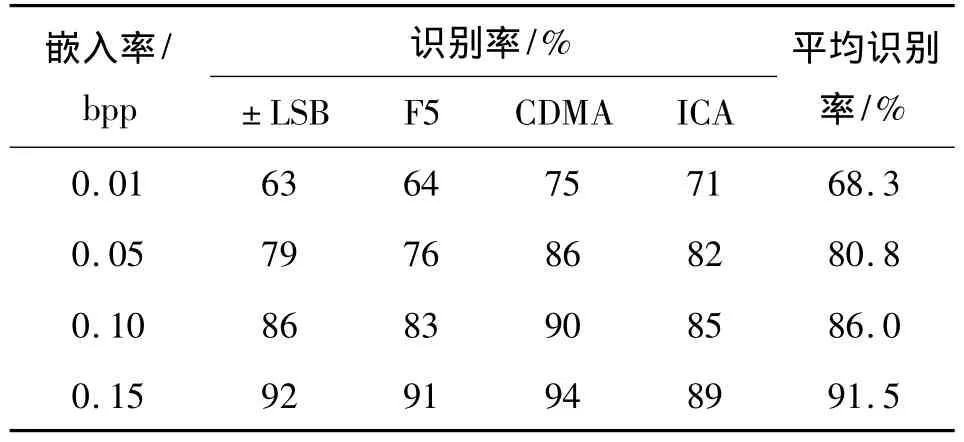
表1 本文方法的识别率

从实验和结果中可以发现:

1)当嵌入率在0.01 bpp时，识别率能达到60%以上;当嵌入强度增加到0.15 bpp，识别率已经达到90%左右，这证明了本章所提算法的有效性。而且随着嵌入强度的增加，识别率也随着上升。这是很自然的，因为嵌入的秘密信息越多，载体图像的质量降低就越明显，也就更容易被检测出来。

2)识别率随嵌入强度上升的幅度是不一样的。当嵌入强度从0.01 bpp提高到0.05 bpp，识别率都增加了10个百分点以上;而嵌入强度再增加，识别率上升的幅度就不明显了。在实验中也继续增大嵌入率，当嵌入率在0.20 bpp以上时，识别率变化不大，再继续实验已经没有意义了。

为了形象直观地说明本文算法的性能，作者分别按照文献［4，5，11］的特征提取方法，在上述的实验图像集上重新做实验，计算各自的平均识别率，实验结果如图1所示。从图1中可以看出，本文所提的算法性能明显优于Farid的经典算法，也同样优于两种类似的算法。

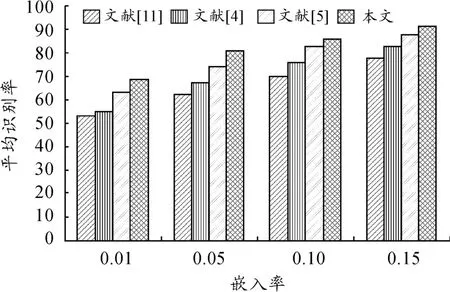
图1 性能比较

4 结论

本文分析了小波高阶统计量的缺陷，从两个方面加以改进，一是引入Contourlet分解，能够更好地表现图像的细节特征;二是采用CDHMT模型，能完整刻画Contourlet系数的相关性。在此基础上提出了一种基于Contourlet域高阶统计量的隐写分析算法。实验结果表明，该算法是一种有效可行的隐写分析算法。

［1］Farid H.Detecting hidden messages using higher-order statistical models:Proceedings of International Conference on Image Processing，2002［C］.2002(2):II_905-II_908.

［2］Do M N，Vetterli M.The contourlet transform:an efficient directional multiresolution image representation［J］.Image Processing，IEEE Transactions on，2005，14(12):2091-2106.

［3］Sullivan K，Madhow U，Chandrasekaran S，et al.Steganalysis for Markov cover data with applications to images［J］.IEEE Transactions on Information Forensics and Security，2006，1(2):275-287.

［4］Hedieh S.A Steganalysis Method Based on Contourlet Transform Coefficients:Proceedings of International Conference on Intelligent Information Hiding and Multimedia Signal Processing，2008［C］.2008:245-248.

［5］Hongping X U，Jianhui X.Steganalysis method based on svm and statistic model in contourlet domain［J］.SPIE.2007，6786:67861C-67864C.

［6］Crouse M S，Nowak R D，Baraniuk R G.Wavelet-based statistical signal processing using hidden Markovmodels［J］.Signal Processing，IEEE Transactions on.1998，46(4):886-902.

［7］Ortega M，Rui Y，Chakrabarti K，et al.Supporting ranked Boolean similarity queries in MARS［J］.Knowledge and Data Engineering，IEEE Transactions on.1998，10(6):905-925.

［8］Sharp T.An Implementation of Key-Based Digital Signal Steganography［J］.LNCS.2001，2137:13-26.

［9］Westfeld A.F5-A Steganographic Algorithm:High Capacity Despite Better Steganalysis［J］.2001，2137:289-302.

［10］Gonzalez-Serrano F J，Molina-Bulla H Y，Murillo-Fuentes J J.Independent component analysis applied to digital image watermarking:Proceedings of International Conference on Acoustics，Speech，and Signal Processing，2001［C］.Salt Lake City，UT，USA，2001(3):1997-2000.

［11］Lyu S，Farid H.Detecting Hidden Messages Using Higher-Order Statistics and Support Vector Machines［J］.LNCS.2003，2578:340-354.