挖掘课本例习题的教学价值，提高数学教学实效

沈良琴

摘 要： 例题习题教学是数学课的主要环节，它的有效性决定着教学目标落实的程度.认真剖析课本例题、习题，对典型的例题、习题从多角度挖掘其典型的应有的教学价值，这样不仅能加深学生对数学概念、法则、定理等基础知识的理解和掌握，还能让学生在解题的准确性、灵活性和敏捷性上得到有效的提高.

关键词： 课本习题 多角度挖掘 变式拓展 教学实效

教材上的例题有最规范的解答过程，具有示范性、典型性和探究性，是课本的精髓，它和习题一起控制了教材的深度和知识辐射范围.教师应充分认识课本例习题所蕴涵的价值，注重对课本例题和习题进行充分的挖掘和研究，对其深化和发展、全方位探索，挖掘其内含及外延，把新旧知识有机组合起来，达到优化认知、开阔眼界、活跃思维、提高能力的目的.

我以苏科版教材中的例习题为例，就数学课堂教学中如何结合教材特点，发掘课本例习题的教学价值，开拓学生思维，提高数学教学实效谈谈体会.

一、构建一节课中完整的例题体系

要想使例题教学的效益最大化，在课前就必须对一节课的“例题”构建一个体系，对例题的数量、类型、前后联系进行整体设计.

例如：我在设计九下教材7.6《解直角三角形》第二课时时，结合课本例题进行了如下设计，例题体现构造直角三角形，选择合适的三角函数求线段的长.

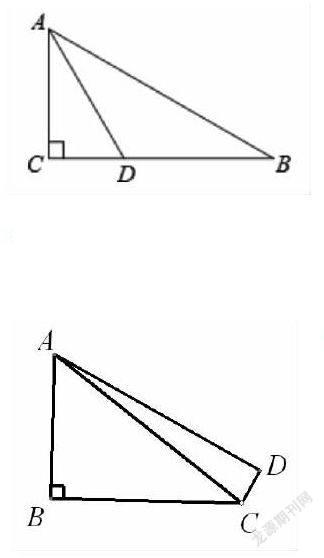
例1.如图所示，△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，若BD=10，求AC长.

例3.如图所示，在四边形ABCD中，∠B=∠D=90°，∠BAD=60°，若CD=2，BC=11，求AC长.

这三道例题层层递进，例1利用“等角对等边”求得AD=10之后，直接利用三角函数可求得AC的长.例2与例1图形相同，所求相同，只是将已知条件做了变化，在Rt△ACD中利用三角函数得到线段之间的比例，根据比设未知数，再在Rt△ABC中利用勾股定理列方程求解.例3需添加辅助线进行解题，延长BC、AD交于点E，三角函数和勾股定理结合便可解决该问题.

二、变式拓展，挖掘例习题的广度和深度

教材中的例题是最好的例题资源，但如何用好这些例题，如何在此基础上进行生发，我尝试以下方法进行例题教学——一题多问，一题多变，多题一解，错题辨析等.

例如：在九下二次函数的应用教学时，我进行了如下设计.

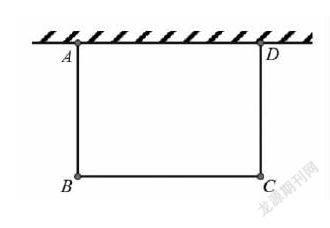
（1）写出S与x之间的函数关系式；

（2）当x取何值时，面积S最大，最大值是多少？

补充提问：若此问题中将“墙的长度足够长”改为“墙的最大可利用长度为15m”，解题的结果会发生改变吗？

（1）请求出S与x的函数关系式及自变量的取值范围.

若能，请求出最大面积；若不能，请说明理由.

这两个例题的问题背景、解决方法有类似之处，题设条件部分发生了改变，所求结论表达形式稍加改编，因此一题多变、多题一讲是很必要的.它可以使学生感觉到知识点的核心之处，只要将它的内涵与外延挖掘彻底，进而灵活运用就可以了.

三、好的例题一定要有匹配度高的练习支撑

例题教学就如扶着孩子学走路，最终孩子要学会自己走路，这一过程必须在相对熟悉的题型中自主尝试，所以好的例题一定要有匹配度高的练习支撑.

为了分解难点我将该题设置了4个小问题：（1）求弦CD的长.（2）弦CD与AB有什么关系，请说明理由.（3）阴影部分面积与半圆的面积有什么关系，请说明理由.（4）若点A是AB上一动点，求阴影部分面积.

该题将要求的阴影部分面积转化为扇形COD的面积，为了计算不规则图形的面积，常常需要变动图形的位置或对图形进行适当的分割、拼补、旋转等手段使之转化为规则图形的和、差关系.我设计了两个习题作为配套练习：

2.圆心角都是90°的扇形OAB与扇形OCD如下图所示那样叠放在一起，连接AC，BD.

（1）试说明△AOC≌△BOD.

（2）若OA=3cm，OC=1cm，求阴影部分的面积.

课本中的每一个例题、习题的设置都有其目的和作用，教学中只有认真钻研教材，领会教材编写意图，深刻理解课本例习题的重要价值，根据教学的要求和学生的实际，将这些例习题进行进一步探究，引导学生全方位、多角度地思考，才能提高数学教学实效.

参考文献：

[1]数学课程标准解读（全日制义务教育）[M].湖北教育出版社，2011.

[2]邵潇野.例谈课本几何习题的拓展研究[J].中国数学教育，2007（10）.

[3]张晓静，邵光华.美国数学教材例习题设计分析与启示.中学数学教学参考，2012（5）（中旬）.