“圆是不是特殊扇形”，非要分出是非来吗？

刘佳 严育洪

【“望”：病例观察】

苏教版五年级下册新教材中，圆的单元新增加了“扇形的初步认识”。为了使学生认识到“在同一个圆上，圆心角的大小决定扇形的大小”，执教教师设计了这样的活动环节——

教师在黑板上画了一个圆，以两条软磁铁为半径，一条固定，转动另一条。演示后提问：你发现了什么？

生1：随着圆心角的变化，扇形的大小也发生了变化。

生2：扇形的圆心角变大，扇形的面积也变大。

教师获得预设答案，正要说下去，谁知又有学生接口——

生3：扇形是圆的一部分，它们是部分与整体的关系。

生4：圆是特殊的扇形，我感觉它们还是特殊与一般的关系。

教师听了生4的回答，有点意外：“你为什么说圆是特殊的扇形？”

生4：圆可以看成圆心角是360°的扇形。

教师一听，感觉有理。

……

【“问”：病历记录】

课后，笔者做了一个测试：首先让学生画一个圆，除了画有直径的圆，还有许多学生的作品如图1；然后让学生接着画一个圆心角是360°的扇形，许多学生的作品如图2。

在评课时，教师们在“扇形是不是圆的一部分”“圆是不是特殊的扇形”这两个问题上争得面红耳赤——

师1：我认为，“扇形是圆的一部分”这一说法是对的，因为教材例题（如图3）就是从圆中截取一部分引出扇形的。

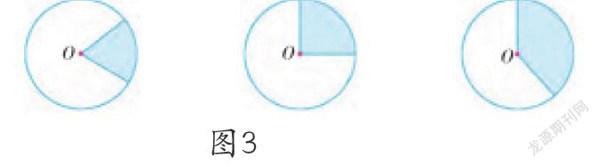
师2：我认为，“扇形是圆的一部分”这一说法不对，因为扇形是由圆周的一部分与它所对应的圆心角围成的图形，它不包括内部的涂色部分。

师1（不服）：那教材例题的要求不是写了“观察各圆中的涂色部分”吗？

师2（解释）：这可以从教材例题下面的小卡（如图4）的提示知道，扇形只指外部的轮廓。

师3（依然不服）：照你这么说，教材小卡下面（如图5）写的“上面各圆中的涂色部分都是扇形”这句话作何解释？

师2（语塞）：是啊，我也被弄糊涂了。“涂色部分”似乎又包括内部的面积了。

……

师4：我感觉“圆是特殊的扇形”这种说法也不对，正如“平行四边形不是特殊的梯形”一样。

师5（质疑）：如果它们不是包含关系，那为何扇形面积计算公式可以适用于圆面积计算公式，同样，为何梯形面积计算公式可以适用于平行四边形面积计算公式。

师4（思考许久）：这个……我也说不清。

……

【“切”：病理诊治】

在《数学辞海（第1卷）》中对“圆”是这样叙述的：圆（circle），平面几何中最基本、最重要的图形之一。圆的定义方式很多，常见的有以下三种：①平面上到定点O的距离等于定长r的全体点组成一条曲线称为以点O为圆心、以r为半径的圆周，简称圆。②到定点的距离等于定长的动点的轨迹称为圆，该定点称为圆心，定长称为圆的半径。③给定一条线段，使其绕着它的一个固定的端点在平面内旋转一周，其另一个端点所经过的封闭曲线称为圆，线段的固定端点称为圆心，线段长称为圆的半径。

根据以上圆的定义，我们不难发现，圆是一条线，而不是一个面，它是“圆周”的简称。也就是张奠宙教授在《小学教学（数学版）》2014年第4期《更多地关注数学本质与细节处理——以圆的定义为例》一文中的观点：“一般认为，圆是一维封闭曲线，具有周长。”

由此观察上述课例，执教教师“在黑板上画了一个圆，以两条软磁铁为半径，一条固定，转动另一条”这一做法，转到最后留下的是这样一个图形（如图6），它是圆心角是360°的扇形。我们把它与圆（如图7）进行比对，不难发现它们“外貌”不同：扇形是由圆的两条半径和圆心角所对的孤围成的图形。扇形的概念包括：①圆的两条半径；③圆心角所对的弧；③由两条半径与弧围成的图形；④扇形是轴对称图形，只有一条对称轴。当扇形的圆心角是360°时，圆心角的两条半径重合在了一起，圆心角所对的弧的长度正好等于弧所在圆的周长。而圆只是指圆周这一条曲线。

至此，我们不难发现，“圆心角是360°的扇形”和“圆”并不是一回事，“圆可以看成圆心角是360°的扇形”这一说法似乎并不正确，由此“圆是特殊的扇形”这一说法似乎也不成立。此时，我们也就可以体会到教材上只写“右图中A、B两点之间的曲线是弧，它是圆的一部分”而不写“扇形是圆的一部分”背后隐藏的道理。也就是说教材是把圆看作圆周的简称，当然，如果教材例题要求把“观察各圆中的涂色部分，说说它们的共同特点”改成“观察各圆中的涂色部分的形状（或轮廓），说说它们的共同特点”，可能更加明确。

可以说，一些学生产生误解就是因为没有吃透圆与扇形的本质含义，除此，还有一个原因是一些学生对圆存在着错误表象，课后的调查已经告诉我们，许多学生脑中的圆是如图8这个样子的——一个画有半径的圆，它貌似圆心角是360°的扇形样子。

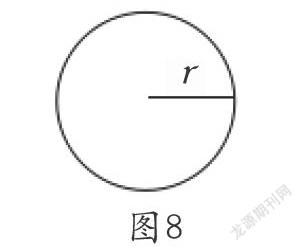
那么，为何一些学生会留下如此圆的形象呢？笔者认为，这与知识的本身和教师的教学有一定关系。在教材编排上，认识圆的一开始就与决定其大小的半径联系在了一起，由此一些学生也就认为半径是圆的一部分，再加上许多教师对圆的认识也比较模糊或不注意对圆的抽象结果，于是造成学生对圆的认识发生偏差。而以前认识长方形就不会有此错觉，因为首先研究的边角，并且决定长方形大小的恰好是围成它的长和宽，认识平行四边形、三角形等平面图形时，决定它们大小的高要在教学它们面积的时候才提及，并且常常被画成虚线。因此，这些直线平面图形的形象在学生脑海里还是比较清晰的。另外，许多教师采用甩小球等动态演示引出圆，连着小球的那一条线以及这条线扫过的面给学生造成了强烈刺激，于是有些学生对圆留下了错误的印象。由此可见，小学教材采用沿着圆形物体一周描出圆的抽象方法，可以避免上述尴尬，一开始就让学生留下圆的正确表象。

当然，还有人是这样来反驳“圆是特殊的扇形”这一说法的：若圆心角为360°时所组成的图形，我们视它为特殊扇形，那么是否也可以将点视为特殊的线段（线段的两个端点重合），从而视三角形是任意多边形的特殊情况呢？再将点视为特殊的圆（R=0时），继而又视圆锥是圆台的特殊情况呢？

如果我们再次研读《数学辞海（第1卷）》中对“圆”的描述，又会发现这样一些文字：“到圆心的距离不大于半径的点的全体通常称为圆盘（或闭圆盘），有时也简称圆。”“总之，圆是圆周和圆盘的统称。”

这些话告诉我们，圆也可以是圆盘的简称。例如教材中所用的“圆面积”，其意应该是“圆盘面积”。此时我们也就能够理解张奠宙教授所说的“一般认为，圆是一维封闭曲线，具有周长”中的“一般”的含义了。众所周知，我国小学数学基本上是从西方移植而来的，英文中的circle我们直译为圆，其含义是一维的曲线。但是英文中还有一个词disk，专指二维的圆形的图形，《英汉大辞典》释义为“圆盘、圆板、圆片、圆平面”。因此，在英文里，圆和圆盘是两个不同的词。但是，在汉语里，两者混同起来了。

张奠宙教授在《更多地关注数学本质与细节处理》一文中提出这样的设想：“圆盘”一词可不可以用“圆形”代替？这是由于三角形、矩形、多边形以及高等数学中的曲边梯形等词语，都是指二维的图形。“圆形草坪”一句中所出现的“圆形”一词，也是用来形容二维的草坪的。因此，借鉴矩形的面积、三角形的面积的说法，使用“圆形”的面积也许是一个不错的选择。这也是许多教师在以往教学中常有的困惑——“为何‘圆’不说成‘圆形’”的缘故。

《数学辞海（第1卷）》中也指出“半圆”与“半圆形”含义不同，“半圆”多指圆周一半的弧，而“半圆形”是指由半圆周和连结它的两个端点的直径所围成的图形。由此可见，如果这样区分，那么“半圆是扇形”应该说成“半圆形是扇形”，或者说成“半圆与直径的组合也是扇形”。

其实，很多情况下，长方形、平行四边形、三角形、圆以及扇形等平面图形，在人的眼里，常常一词两义——在周长和面积之间切换，正如《数学辞海（第1卷）》中的补充说明：“在平面几何中，圆一般多指圆周。在不同的学科和不同的场合，将圆理解成圆周还是圆盘，要视具体情况而定。”在平常使用中，当它们表示面积的时候，我们习惯说“长方形面积”而不说“长方形面面积”， 习惯说“圆面积”而不说“圆盘（面）面积”，习惯说“扇形面积”而不说“扇面面积”等。当圆指称圆面、扇形指称扇面的时候，“扇形是圆的一部分”“圆是特殊的扇形”等说法似乎又不可说不对。

扇形，一般情况下指一周的轮廓。《数学辞海（第1卷）》中对“扇形”是这样定义的：指由一条圆弧和过这条弧的端点的两条半径所组成的图形。初始认识扇形时，我们还是应该把概念建立在“一般情况下”。由此观察教材例题（见图9），可能会发生像课后访谈中教师的质疑——“‘上面各圆中的涂色部分都是扇形’这句话该怎么解释？”

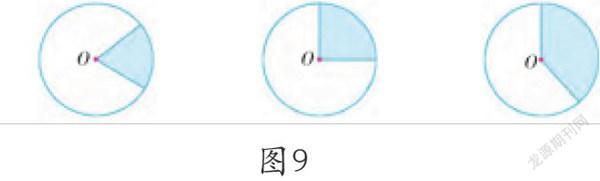
对照教材例题下面小卡的提示语（见图10）和教材最终呈现的扇形几何图（见图11）， 我们大致可以明白教材编写的意图：“上面各圆中的涂色部分都是扇形”是知识的过渡，为了从圆（此处“圆”的含义应是“圆盘”或“圆形”）中截取出扇形（此处的“扇形”的含义应是“扇面”），然后让学生观察特征，最终抽取出扇形是由圆周的一部分与它所对应的圆心角围成的图形。《几何原本》这样定义扇形：“由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形。”由此推想，教材可能想采用截取的意味来描述扇形的定义，毕竟扇形与圆有着密切的联系，有的地方把“扇形”称为“圆扇形”。当然，如果把“上面各圆中的涂色部分都是扇形”说成“上面各圆中的涂色部分的形状都是扇形”，可能更会让学生明白扇形的一般意义。

上述课例中，生4认为“圆是特殊的扇形”的理由是“圆可以看成圆心角是360°的扇形”，也就是当扇形的圆心角增大到360°时，它是一个面积等于同半径圆面积的特殊扇形，这是一种极限思想。这里观察的对象是它们的面积，因此说成“圆心角是360°的扇形面积与同半径圆面积相等”可能更为明确。

当“圆是特殊的扇形”表示“圆面是特殊的扇面”时，对学生学习最大的好处是能把扇形面积计算公式同圆面积计算公式实现沟通与统一，减少记忆负担。同理，“平行四边形是特殊的梯形”表示“平行四边形面是特殊的梯形面”时，那么梯形面积计算公式就能够同平行四边形面积计算公式实现沟通与统一。

然而，在一般意义上，“平行四边形是特殊的梯形”在学术界又是一番争论。根据梯形的一般意义“只有一组对边平行的四边形，叫作梯形”，毫无疑问，平行四边形不是梯形。不过，当看了持“平行四边形宜为特殊的梯形”的人所提出的以下这些“证据”，我们又不免会发出这样的感叹：“‘平行四边形是不是特殊的梯形’真的有那么重要吗？把平行四边形归为特殊的梯形又何妨！”

（1）从图形所具有的性质来看，梯形所具有的一些公式、性质，平行四边形也都具有。

（2）从图形的运动轨迹角度来看，如图12所示，

如果A点（或B点）向B点（或A点）运动或做反方向运动，当且仅当AB=CD时，四边形ABCD为平行四边形，其余的情况都是梯形；同样，如果C点（或D点）向D点（或C点）运动或做反方向运动，当且仅当AB=CD时，四边形ABCD为平行四边形，其余的情况都是梯形。

（3）从知识的逻辑性角度来讲，“有一组对边平行的图形叫作梯形”定义的优点，在于它是清楚地按照逻辑分类叙述的，“只有一组对边平行的图形叫作梯形”定义则不是用的一种标准，而是同时采用了逻辑分类的两个连续阶段：首先是一组对边的性质，然后是另一组对边的性质。它不应该同时采用，而应该是顺次的。采用了第二种定义，我们便失掉了逻辑的清晰性。张奠宙教授在《小学教学（数学版）》2015年第6期《正本清源，力求正确——关于数学教材中“分类”单元的评论》一文中，对四边形按边角关系的等级分类（见图13），我们可以看出他也是把平行四边形归为特殊的梯形。

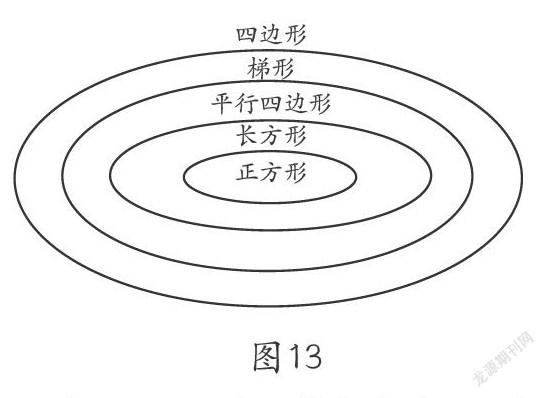
（4）从知识研究过程的角度来看，我们研究事物经常用到的方法是从特殊到一般，然后用一般的方法或结论去解决特殊的问题。对于四边形的研究，我们是从正方形（特殊的长方形）与长方形（特殊的平行四边形）开始，接着是平行四边形（特殊的四边形），然后是梯形（特殊的四边形）。也就是说，如果我们对四边形的研究采用常用方法，即从特殊到一般：正方形—长方形—平行四边形—梯形—四边形，那么，平行四边形就宜为特殊的梯形。

（5）从数学的简约性角度来看，把平行四边形归为特殊的梯形，可以使四边形的分类由目前的一分为三，即四边形包括一般的四边形、平行四边形与梯形，简化为一分为二，即四边形包括一般的四边形与梯形，这样便于学生的研究与记忆。所有梯形的性质，很自然地（也就是不必再加证明）使用在平行四边形上，例如梯形中位线的性质。

当然，反对“平行四边形宜为特殊的梯形”的人所持的论点是，如果把平行四边形作为梯形，那么它就包含了等腰梯形。但是在以后证明的很多等腰梯形的性质，都是平行四边形所没有的，如等腰梯形的底角彼此相等，等腰梯形的对角线彼此相等，等腰梯形可有一外接圆等。如果把平行四边形认为是等腰梯形，那么在上述的所有定理之中，在“等腰梯形”一语之后，都应增加“如果它不是平行四边形”的条件。为了避免这种麻烦，某些教学法专家宁可事先把平行四边形从梯形中去掉。对此，倡议者提出可以通过两种方法来解决：一是在所有的定理中，增加上面所说的条件，二是一劳永逸地把这条件加在等腰梯形的定义中，也就是这样来定义：“两腰相等但不平行的梯形，叫作等腰梯形。”

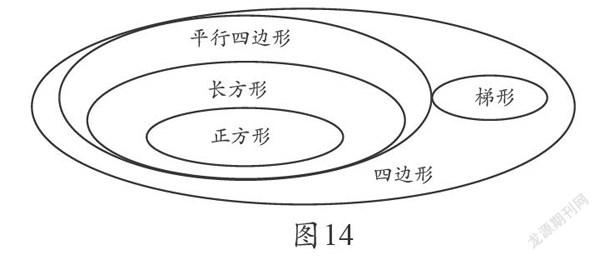
有人说，数学有时“粗”一点好，有时不一定非要分出是非来。我们可以按照现行教材普遍采用的如图14这种便于学生理解的分类方法进行概念教学，在之后的面积教学中，再顺便指出梯形面积计算公式对于计算平行四边形面积（包括长方形面积以及正方形面积）、三角形面积都适用，在此意义上，平行四边形和三角形都可看作梯形的特殊情况。

总之，数学教学非常讲究每隔一定的学习阶段就从一种较高的视角来统观全局，统揽前面所学过的互相关联的各种知识。如果我们用“联系”的观点来考察知识，我们就会发现，打通知识之间的壁垒远比非要分出知识的是非来要有意义得多，它能够让我们跳出知识的“界限”，从更广的知识背景下看到更远的知识风景。例如我们可以用梯形面积计算公式统一平行四边形面积和三角形面积，但我们如果换一个视角，还可以发现平行四边形和三角形的面积计算也容纳了梯形面积计算的方法，这就是中位线法——面积=中位线长×高。此时，谁还会去纠结它们之间的关系——谁是特殊谁是一般，而只会惊叹它们之间的联系——知识真奇妙！

（江苏省宜兴市城南实验小学 214200 江苏省无锡市锡山教师进修学校 214191）

编后语：“圆是不是特殊的扇形”“三角形是否可看作梯形的特殊情况”“平行四边形是不是特殊的梯形”是专家、教师经常探讨的话题。诚然，一般讨论的焦点都会落脚到“是”或“不是”的结论上。本文作者在综合分析各家观点的基础上提出了“数学有时‘粗’一点好，有时不一定非要分出是非来” 的观点。他认为如果用“联系”的观点来考察知识，就会发现打通知识之间的壁垒远比非要分出知识的是非来要有意义得多，它能够跳出知识的“界限”，从更广的知识背景下看到更远的知识风景。对于这样的观点，你是否认同呢？欢迎大家参与讨论！