在操作中丰富体验

戴美兰

《义务教育课程标准实验教科书？摇数学》第七册教材安排有一个课题为“怎样滚得远”的综合与实践的教学内容。对于这种操作性强的实践活动内容，孩子们的学习积极性非常高。课一开始，我就用电视媒体播放生活中有关物体滚动的情景，然后提出疑问：有一个圆柱形易拉罐（放在搁板上），你有什么办法使它在桌面上滚动？今天我们要通过小组合作实验的方法研究在什么角度时，物体滚得远。话音刚落，教室里就沸腾了。我立即请两位学生与我合作，示范实验方法：搭一搭，滚一滚，量一量。在学生有了清晰感知后，我把学生分为四个小组，小组明确分工，小组成员接受任务（包括：组长、物体滚动者、角度和距离测量者和记录员）。在明确实验要求和注意点后，各小组学生立即开展实验，把木板分别调整到30度、45度、60度进行实验，每个角度操作三次，做好记录后，计算出平均数并完成填表。我在旁边巡视并作相应指导和调整，看到学生的实验在有条不紊地展开，我心里暗暗高兴。很快，实验结束了。

各小组学生反馈交流：第一、第二、第四组都认为木板的角度与地面成30度时物体滚得最远；第三组认为木板的角度与地面成45度时物体滚得最远。我适时引导：根据刚才的实验结果，你们有什么疑问和猜想吗？李明：我的疑问是，为什么角度大的会滚得近？王玲：我觉得应该是角度越小就滚得越远。杨红：我也是这么认为的……大部分学生都点点头，第三组的学生这时可不敢提出异议了，默认了大家的看法。我说：同学们，既然你们都认为角度越小物体滚得越远，就请你们自己再设计一个实验来验证猜想吧。学生讨论后就选了一个15度的角，实验如火如荼地进行着，这时奇怪的事情发生了。四组学生都发现15度时物体反而没有30度时滚得远了。凌萍抢着说：我们小组发现小于30度时滚得并不远。周阳：我们觉得还是30度时最远……这是怎么回事？学生有些茫然了，两次实验得到的结论并不一样，甚至有些背道而驰。看着那一张张带着疑惑的小脸，我只能大手一挥：同学们，刚才我们做实验时由于受到场地、滚动物体、测量误差等一些因素的影响，最后没来得及找到正确结论，我们下次继续研究。

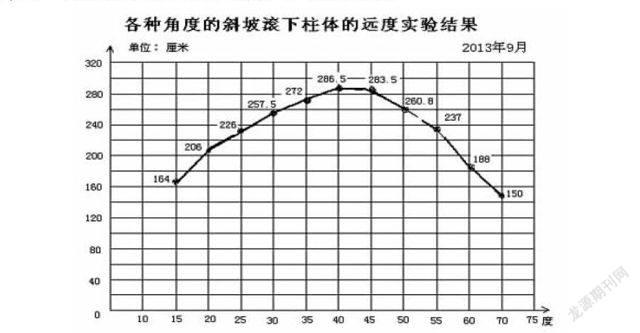
下课铃声响了，学生的收获是模糊的，我长长地叹了一口气。究其原因，主要是我课前准备不充分，对实验中可能会出现的情况估计不足，对什么角度下物体滚得远认识也比较模糊。我和几位同事决定进行“下水实验”。实验对场地和滚动物的材质等干扰因素作了控制，只考虑坡度、角度变化作为自变量，对实验结果整理并制作了统计图。

第二天数学课上，我笑容满面：同学们，今天你们想继续做实验，继续探究吗？别急，根据上次的实验，小组先讨论讨论，当木板与地面的角度成（？摇 ？摇）度时，物体有可能会滚得更远？

王红：我们小组觉得当木板与地面的角度成20度时，物体有可能会滚得更远些。

孙杨：我们小组觉得当木板与地面的角度成40度时，物体有可能会滚得更远些。

莉莉：我们小组觉得当木板与地面的角度成50度时，物体有可能会滚得更远些。

季明：我们小组觉得当木板与地面的角度成45度时，物体有可能会滚得更远些。

邵洁：……

大家又开始争论起来，谁也说服不了谁。这时，我们班的智多星孙亮站起来：你们不要争了，我觉得，通过前两次实验，我们不能只想着木板与地面的角度成几度时物体滚得更远些，有没有可能，木板与地面的角度在某一个范围内，物体都滚得比较远。一石激起千层浪，大家如梦初醒，纷纷说：对呀，对呀，我们怎么没想到呢？

我适时引导：那，你们四个小组做一下分工吧。第一小组准备选取几度角开展实验？第一小组选取了20度、25度的角，也就是选取小于30度的角度再次实验。第二小组选取了35度、40度的角，也就是选取30度与45度之间的角度再次实验。第三小组选取50度和55度的角，也就是选取45度与60度之间的角度再次实验。第四小组抢着说：我们不选60度以上的角，我们和第三小组一样选。我作疑惑状：为什么呀？大家都笑了，抢着回答：因为上次实验时我们发现60度时物体滚得最近，所以我们觉得60度以上的角度时物体肯定也滚得不会远。我发出会心的微笑：有道理，看来你们都是善于观察、善于思考的孩子，那就请你们根据刚才选择的角度再次开展实验吧。很快，第二轮实验在组长与组员的配合默契中展开了。他们忙着搭建角度，滚动易拉罐，记录实验数据，计算平均数，填写实验表，忙得不亦乐乎。总结交流时，孩子们的发言精彩极了。

第一小组：我们觉得小于30度时物体并不滚得远。

第二小组：我们觉得在30度～45度之间物体滚得都比较远。

第三小组：我们觉得在45度～60度之间物体也滚得并不远。

第四小组同上。我不急着发表意见：请你们仔细观察四个小组的实验数据，把两次实验数据对比并讨论讨论，看看有什么发现？

大家一致认为物体在30度～45度之间时滚得远。他们的脸上都露出了胜利的微笑。

这次实验活动，孩子们表现出的动手操作能力、小组合作能力、观察力、思维力，让我为之惊讶和感动。在数学学习中，孩子们会遇到各种各样的问题，老师要多为孩子提供机会，创造条件，让他们通过自己的努力解决生活中的数学问题。

荷兰教育家弗赖登塔尔说过：数学是一种人的活动，如同游泳一样，要在游泳中学会游泳，我们也必须在做数学中学习数学。课上，我抓住学生感兴趣的生活现象和问题引导小组合作，共同完成“滚动”活动，在动手和动脑中积累活动经验，发展数学思考，提高学习兴趣。我只是在教学的关键点、学生的疑惑点、疑难处加以引导。

“经历过程”、“关注过程性目标”是新课标的一个显著特征。经历过程不单单是为了获得知识和技能，更重要的是带给学生探索的体验、创新的尝试、实践的机会和发现的能力，这些都比具体结果的获得更重要。我给予了学生自由的活动时间和空间，让学生大胆实验、猜想、交流、再实验、再交流，让学生在多次的实验活动中积累丰富的探究经验，感悟如何通过比较分析实验数据获取科学结论的学习方法。学生在参与中有了更多交流与合作的机会，创新思维和能力也得到了培养与激发。