坐标法在向量最值问题中的应用

卢春明

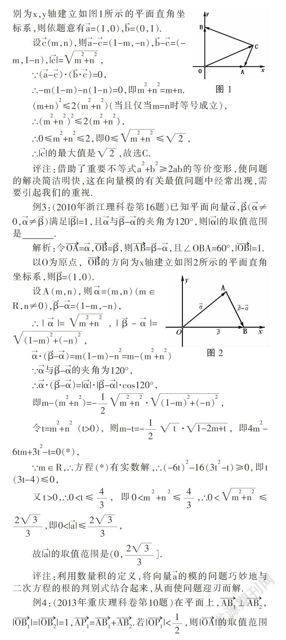
在近年高考中，向量由于其具有数、形结合的双重特性越来越受到命题者的青睐，尤其是与平面向量最值相关的题型精彩纷呈，极富挑战性.此类问题的解法众多，颇有“百花争艳”的意味，有些问题利用几何法甚至可以达到“秒杀”的效果，使人赞叹不已，但不管是当年的考生还是现在的同学，这类问题却常成为他们的“滑铁卢”，让人扼腕叹息.

究其败因，正是向量的抽象性使问题的理解出现了困难，如何突破这一障碍显得异常重要.“坐标法”可以使向量运算完全代数化，使问题的求解变得简单易行，这就是一把“金钥匙”，不管它是数量积的最值问题，还是向量模的最值问题，一切处理起来都会显得那么直观、自然.

本文从两个不同的角度展示了“坐标法”对处理平面向量的最值问题的独特作用，希望能给读者对向量问题的求解提供启示和帮助.

一、不建系，直设坐标

传统意义上的“坐标法”在应用时，往往必先建立起坐标系，这让我们不得不在题意中寻觅建系的合适条件，而对于某些没有任何“几何条件”的问题，很容易陷入困境，甚至让人不知所措.实际上，每一个向量在平面直角坐标系内都可以用一有序实数对唯一表示，这启发我们：在利用向量的坐标运算解决问题时，坐标系如何建立有时并不重要，只需将向量置于平面直角坐标系内即可.

坐标法的应用，使我们更容易地触及向量最值问题的本质，不仅避免了繁杂的逻辑推理，而且加强了数形结合思想在解题中的运用，值得借鉴.

参考文献：

[1]程坚.利用对称巧建系简化运算显神奇.数学通讯（上半月），2014（1，2）.

[2]陈燕.多视角探究平面向量最值问题.数学通讯（上半月），2014（4）.