利用课堂教学提高数学思维能力

卢桂英

摘    要： 课堂是对学生进行思维能力训练的主阵地，在数学课堂教学中要将学生数学思维能力的培养落到实处。

关键词： 数学课堂教学    数学思维能力    多边形内角和

思维是人类特有的一种复杂心理活动，其中数学活动中的归纳、类比、转化等思维方法，都具有广泛的应用性。数学本质上就是一种探索性的创造活动。数学思维能力的培养是一个长期的过程，而课堂是对学生进行思维能力训练的主阵地，在教学中要将学生数学思维能力的培养落到实处，应该做到两点：一是精心设计问题启发学生思考;二是重视创设让学生自主思考、作出选择、判断和调整的时间和时机。下面我以新人教版八年级上册《多边形的内角和》为例谈谈体会。

一、探索四边形内角和

1.分割法

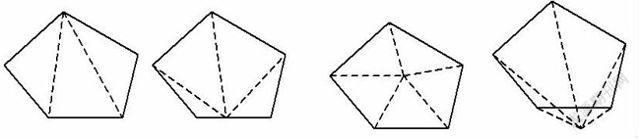
探索四边形的内角和，学生容易想到连接一条对角线，把四边形转化成三角形来解决，往往不会用其他方法转化。实际上如果把这条对角线的一个端点不动，移动另一个端点“O”的位置，就会产生出多种的分割方式，这里蕴含着丰富的思维过程中。若给予揭示，让学生亲自参与到“O”的探索发现过程，将会使学生受益匪浅。正如徐利治教授所言，学生的思维本质上和数学家的思维是一致的。为此我们可以提出：（1）问题目标是什么？（2）我们已经学过什么多边形的内角和？（三角形，长方形）（3）既然化归的目标已经明确，那么还有哪些转化的方法？（4）为什么要取一点（而不是两点），这点可以在顶点，那么还可以移到哪个位置？

至此学生思维开始活跃，各种归纳方法层出不穷，归纳起来有以下几种。

这里渗透着分类思想（点与多边形的位置关系）和转化思想（把四边形的问题转化成三角形的问题）。

2.补形法

前面我们已经归纳了四种方法，但归纳起来它们都是把四边形分割转化成三角形，图形除了分割外那我们还可以怎样处理呢？这个点如果忽略，学生的思维就没办法再扩展，所以在这个地方应该引导从“分割”到它的相反面“补形”。为此我们可以设置问题：（1）前面我们已经用了四种方法，但它们之间有共同点吗？（2）图形的“分割”相对的是什么？（3）能尝试用图形的“补形”去做吗？引导学生从分割到补形成三角形，至此学生思维被激活。

∵∠1+∠2+∠3+∠4+∠E+∠B+∠C=540°

∴∠2+∠4+∠B+∠C=540°-（∠1+∠3+∠E）=360°

3.作平行线法

我们已经把四边形用分割和补形的方法都成功地把四边形转化成了三角形，启发学生再回忆知识除了知道三角形内角和外还知道什么角度，从多边形的框架内迁移到平行线的知识，两直线平行同旁内角是互补的。转化思想是数学思想方法之一，在这节课堂上可以引导学生体会这种数学思想。因此可以做如下启发：（1）前面我们已经归纳了两种方法寻找四边形的内角和，但这两者有相同点吗？（2）前面两种都是把四边形的内角和转化成三角形内角和，为什么要这样做呢？（3）除了三角形内角和现在已知，还知道什么角度呢？通过这几个问题把四边形的内角和转化成平行线的同旁内角的和，学生思维再一次被激活。

过点A作AE∥BC交DC于点E，

∵AE∥BC，∴∠2+∠B+∠3+∠C=360°，又∵∠3=∠1+∠D，∴∠DAB+∠B+∠C+∠D=360°.

二、探索五边形、六边形内角和

学生有了探索四边形的内角和的经验，只要引导学生用类比的方法进行五边形的内角和的探索。比较容易就能用相仿的方法把五边形、六边形转化成三角形或平行。这也是对前面学过的方法巩固和迁移。以五边形为例：

1.分割法

2.补形法

∵∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠A+∠F+∠G=5×180°=900°

∴∠1+∠3+∠5+∠7+∠A=900°-（∠2+∠4+∠F+∠6+∠8+∠G）=540°.

3.作平行线法

过点B作BG∥CD交AE于点G，过点E作EH∥CD交BC于点H.

∵BG∥CD，∴∠5+∠C=180°，∵EH∥CD，∴∠4+∠D=180°，∵BG∥CD，EH∥CD，∴BG∥EH，∴∠2+∠3=180°，∴∠5+∠C+∠4+∠D+∠2+∠3=540°.

又∵∠2=∠1+∠A，∴∠A+∠ABC+∠C+∠D+∠AED=540°.

三、探索n边形内角和

有了探索四边形、五边形、六边形的内角和的过程，再来总结n边形内角和，这时可让学生任选一种较快的方法进行总结，锻炼学生的归纳总结能力。

学生充分参与到多边形的内角和的探索过程中，体会数学中的分类、转化、化归的思想方法。我们在数学教学活动中，在概括概念本质属性，探索解决问题策略，寻求方法，揭示规律时等都应精心设置问题，要给予学生独立思考问题的时间和时机，绝不能以我们的思维代替学生的思维过程，只有这样学生的数学思维能力才会有更大的提高。

参考文献：

[1]沈倩文，臧雷.数学思维能力及其教学工艺探究.数学教师，1997.06.

[2]徐利治.徐利治谈数学方法论.2008.1.1.7.