一道习题引发的思考

吕敏 夏俊

“统计与概率”的内容在《义务教育数学课程标准（2011年版）》中作了较大调整，学习层次性更加明确，也更加强调了培养学生数据分析观念的重要性。细细品味，该板块内容对学生数学能力的全面发展具有重要意义，它带给学生应对数据时的一种态度与策略，带给学生一种更加宽广的思考方式，而这一切都基于数据分析观念的养成。

但是，在统计图教学中又如何具体开展数据分析呢？在具体的课堂中学生分析数据的现状又是怎样呢？本文笔者通过对一道习题的深入分析、思考，总结数据分析观念养成的具体策略与途径。

一、习题呈现

四年级下学生在学习了“单式折线统计图”后有这样的一道习题。

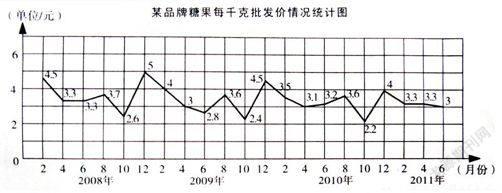
下面是一种糖果几年来各个月份的批发价统计情况。

问题：

（1）从统计图中可以看出，（    ）年（    ）月的批发价最高，（    ）年（    ）月的批发价最低。

（2）从统计图中，你还发现了哪些信息？

（3）如果你是超市经理，2011年哪个月应该多进货，为什么？

问题（1）学生的错误率较低，答案也较统一。问题（2）（3）学生的解答可谓是五花八门，这也引引起了笔者的关注，现整理如下：

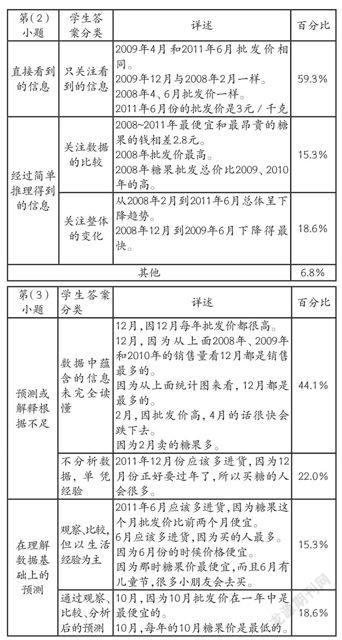
第（2）

小题 学生答案分类 详述 百分比

直接看到的信息 只关注看到的信息 2009年4月和2011年6月批发价相同。

2009年12月与2008年2月一样。

2008年4、6月批发价一样。

2011年6月份的批发价是3元/千克 59.3%

经过简单推理得到的信息 关注数据的比较 2008～2011年最便宜和最昂贵的糖果的钱相差2.8元。

2008年批发价最高。

2008年糖果批发总价比2009、2010年的高。 15.3%

关注整体的变化 从2008年2月到2011年6月总体呈下降趋势。

2008年12月到2009年6月下降得最快。 18.6%

其他 6.8%

第（3）小题 学生答案分类 详述 百分比

预测或解释根据不足 数据中蕴含的信息未完全读懂 12月，因12月每年批发价都很高。

12月，因为从上面2008年、2009年和2010年的销售量看12月都是销售最多的。

因为从上面统计图来看，12月都是最多的。

2月，因批发价高，4月的话很快会跌下去。

因为2月卖的糖果多。 44.1%

不分析数据，单凭经验 2011年12月份应该多进货，因为12月份正好要过年了，所以买糖的人会很多。 22.0%

在理解数据基础上的预测 观察、比较，但以生活经验为主 2011年6月应该多进货，因为糖果这个月批发价比前两个月便宜。

6月应该多进货，因为买的人最多。

因为6月份的时候价格便宜。

因为那时糖果价最便宜，而且6月有儿童节，很多小朋友会去买。 15.3%

通过观察、比较、分析后的预测 10月，因为10月批发价在一年中是最便宜的。

10月，每年的10月糖果价是最低的。 18.6%

二、追踪成因

针对第（2）小题，在发现信息的过程中，学生的回答其实都无关对错，这是由统计教学中问题的开放性决定的，学生切入点的不一致直接产生多样化的观察结果。

细细思考学生选取的“切入点”，我们能大致发现学生观察的结果可分为三大类，即“只关注看到的信息”“关注数据的比较”“关注整体的变化”，其中关注直接看到的信息的同学占了大多数（59.3%）。经访谈，笔者惊讶地发现，很多学生针对“发现了哪些信息”这个问题时，长期以来视野比较狭窄，有相当部分的学生从未想到过要从“数据的比较”和“数据的整体变化情况”这样的角度去看待数据。

“统计与概率”教学几乎每一学年都有，从最初的象形统计图，到条形统计图，再到折线统计图、扇形统计图，为什么还有这么多学生在得到信息时只能读出统计图中直接看到的信息呢？

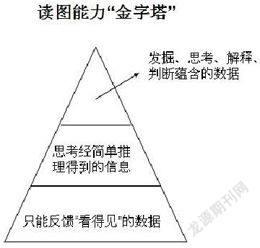
我们不妨从学生的思维特征角度来进行分析。学生在分析数据的过程中，对统计图的认识层次差异其实比较大，大致可以分成如图三个层次。

作为读图的最基础层次，学生能反馈“看得见”的信息，当学生能积极思考经简单推理得到的信息，能进行数据的比较和数据的整体变化的判断时，学生对统计图就有高一层次的认识了，当学生能对数据进行进一步分析，并运用其去思考、去解释、去判断时，学生对统计图的认知就更进一步了！

分析第（3）小题，其中有66.1%的学生所作出的预测或解释根据不足，过多的数据使学生在观察时更倾向于局部而不是整体。学生对某些点所表示确定意义的理解要远远强于对数据整体的判断。同时，竟有44.1%的学生对“批发价”不理解，“批发”这种在生活中司空见惯的事情，学生却不甚了解。究其原因，学生在数学课堂上不曾经历过，没有直观体验才是问题的关键。学生在解决大数据问题时的态度与方法并不是一蹴而就能学到的，关键是在长期的教学中，教师是否关注到学生对过程的参与、整理和思考。

分析中还隐隐暴露出学生存在的一个问题：过于依赖已有经验。“统计与概率”知识中的不确定性并不是完全由个人经验不同而带来的。教学实践中，在改造学生的已有经验方面，我们的关注度还是太低！上述所有问题似乎都指向我们的课堂，那么教师在课堂教学中具体该如何发展学生的读图能力、培养学生的数据分析观念呢？笔者有以下几点建议。

三、教学建议

（一）教师应帮助学生灵活运用“定量刻画”与“定性推断”

“定量刻画”是指学生在面对统计图时对其中的具体值、点、所占大小的理解，包括数据的比较（多少、倍数、百分比等）和数据的整体变化的判断（最大、最小、变化情况等）。“定性推断”是指对柱形的高低比较、线的走势、百分比的意义等的大致感受与答题判断。当“定量刻画”积累到一定程度时，为了促进量变向质变的转化，教师应该及时进行引导，帮助、鼓励学生有依据地作定性推断。值得一提的是，学生们在刚接触统计与概率的知识时也主要是一些大致感受的判断，这与本文所说的“定性推断”的重大区别就在于是否建立在分析数据的基础上，或者说是否建立在“定量刻画”的基础上。定量刻画与定性推断两者是相互影响、相辅相成的！

【教学案例一】

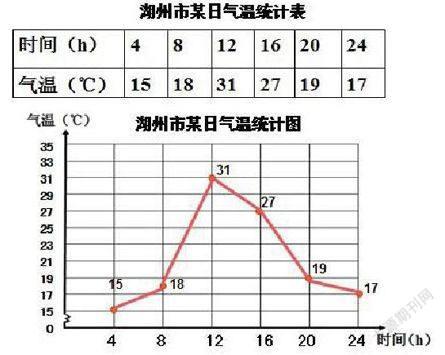
1.出示湖州市某日气温统计表。

时间（h） 4 8 12 16 20 24

气温（℃） 15 18 31 27 19 17

从统计表中你能看出是统计什么吗？

师小结：怎样让信息看起来更加直观？（根据统计表能画出统计图）

2.出示折线统计图。

①你见过这样的统计图吗？（揭题：折线统计图）

②你想掌握什么内容？（为什么叫折线统计图、怎么画、作用）

3.整体感知折线统计图。

①关注线。（隐去每个气温数据）从这条线上你看懂了什么？你是怎么看出来的？（线—温度的变化：上升→增加，下降→减少）从几点到几点气温上升？从几点到几点气温下降？

②关注点。（局部突出）除了从线上看出气温在上升，还能从什么角度看出气温在上升？这些点分别表示什么？

③你还能说出哪个点的意思？（根据学生的回答将点完整标注在折线统计图上）

师小结：点和线是折线统计图最基本的组成部分。

该材料在运用的过程中，从学生熟悉的气温入手，温度的变化趋势有升有降，更完整地展示出温度变化的“全貌”， 让学生“有话可说”。相比传统教学一般从条形统计图入手，这个教学案例更多地是在整体感知与具体把握上花功夫，即运用“定量刻画”“定性判断”来帮助学生直观、形象地认识折线统计图中点与线的意义。在应用过程中，通过问题引导，学生关注到增减的快慢，通过对“所占格子的多少、数据相差程度、线的长度、倾斜的情况”的思考，加深学生对折线统计图中“线和点”的认识，并学习如何运用数据作出合理判断。这样的思考方式能促使学生逐步形成更加全面的数据分析策略与方法。

（二）教师应帮助学生学会分析数据的大势（求同），同时注意特殊数据的分析（存异）

身处这个时代，教师应该有一个清醒的认识：这个大数据时代充斥着海量、零碎的信息，但正是基于对这些数据的处理所产生的规律性使得我们的生活可以有一定的预判，每一个零散数据又显得如此重要。回到小学数学课堂里，这就是我们所说的随机性。当我们带领学生分析大量数据时所呈现出来的大势可以看出规律性，因此随机性并不是毫无规律可循，同时，我们也应该让学生充分感受到确实存在个别数据可能严重偏离预期，但不会影响对整体的判断。

这是对学生已有经验（事物是确定的）的一次重大改造，具体来说也是发展学生更高层次的读图能力的一个方面！

【教学案例二】

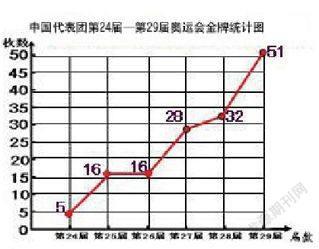
第24届～第29届奥运会中国获金牌数统计表

届数 24 25 26 27 28 29

金牌数（枚） 5 16 16 28 32 51

1.绘制成折线统计图。

①你准备怎么画？

② 28届、29届的金牌数换一下行不行？

师小结：原来横轴上的时间是按顺序排列的，所以我们也应按顺序连！

2.合理预测，体会数据的随机性。

①从这幅统计图上你获得了哪些信息？

②哪两届获金牌数增长得最快？你是怎么看出来的？

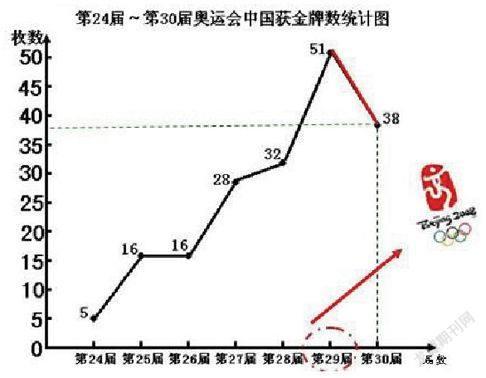
③请你预测一下第30届奥运会中国有几枚金牌？（猜→出示第30届伦敦奥运会中国得金牌38枚、出示第29届北京奥运会中国得金牌51枚）是不是体育水平在下降？

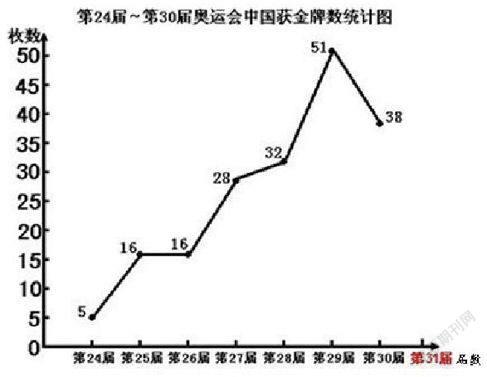
④请你预测一下第31届巴西奥运会中国有几枚金牌？

师小结：根据折线统计图，我们能清楚地看出金牌数的变化趋势，还能作出一定的预测，但是预测的结果是不确定的。

在分析数据的过程中，当学生的思考是建立在分析基础上时，结果就相对合理。先猜测第30届奥运会的情况（其实就是伦敦奥运会，已发生），然后出示比赛结果，对比北京奥运会，让学生感受到数据是不确定的，然后让学生猜测第31届奥运会的情况。学生对数据变化的猜想经历了随意—慎重的过程，步步为营的猜想又促进了学生的思考，学生自觉地对数据进行简单分析，学生的猜测也更有根据！

总而言之，我们所说的数据分析观念是有一定的维度的，反映在课堂上，教师应有更加全面的认识，努力促使学生的读图能力向更高层次水平发展，同时我们也应清楚：了解现实问题应当先做调查研究，搜集数据，这虽不是本文的重点，但它是统计开始的地方，这个过程亦是相当重要！

（浙江省湖州市长兴县李家巷镇中心小学   313102

浙江省湖州市湖师附小教育集团   313000）