推广Klein-Gordon方程新的精确行波解
马云峰,高发玲
(青岛理工大学琴岛学院)
0 引言
Klein-Gordon方程出现在相对论、量子力学、旋转波及非线性光学等理论中.它描写自旋为零的标量粒子的相对性,由于粒子没有自旋、只有一个分量,描述spinless颗粒.若u代表相对论的自由粒子能量,则Klein-Gordon方程可以从相对论性质能关系和薛定谔方程中得到[1].
研究非线性偏微分方程中精确解问题的方法甚多,如齐次平衡法、扩展的(G'/G)展开法、双曲函数法、扩展的F-展开法、扩展的辅助方程法等[2-6],通常采用的辅助方程法为三角函数型,椭圆型,Bernoulli辅助方程法等[7-10].非线性方程具有特殊性,不可能用一种方法求出所有方程的精确解,所以对特定方程选择合适的方法求精确解显得尤为重要.
考虑推广的Klein-Gordon方程为
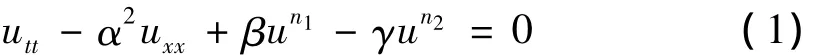
其中α为实常数;β,γ>0为实常数;n1,n2为正整数且u=u(x,t):R×R→R是未知函数.方程(1)中,当n1=1,n2=3时整体解的存在性、精确解的求法及解的性质已有较完善的结论[11-13].但对推广的 Klein-Gordon方程(1)的精确解求法的研究,还未得到展开.该文尝试用扩展的椭圆型辅助方程法求精确行波解,因n1=2,n2=1时的精确解已解决,在此不予讨论.
1 扩展的椭圆型辅助方程法[14]
该文利用辅助常微分方程来构造推广的Klein-Gordon方程精确行波解,主要步骤如下:

非线性发展方程的一般形式可以写为其中,N是关于变元u,ut,ux,utt,uxt,uxx,… 的多项式.
引入行波变换
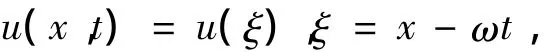
其中ω是非零的待定常数,可将(2)式方程转换为仅关于变量ξ的标准的常微分方程

为了得到方程的精确解析解引入z(ξ),z(ξ)满足
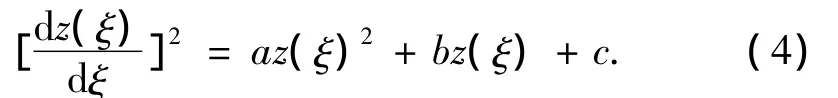
该常微分方程有以下解:

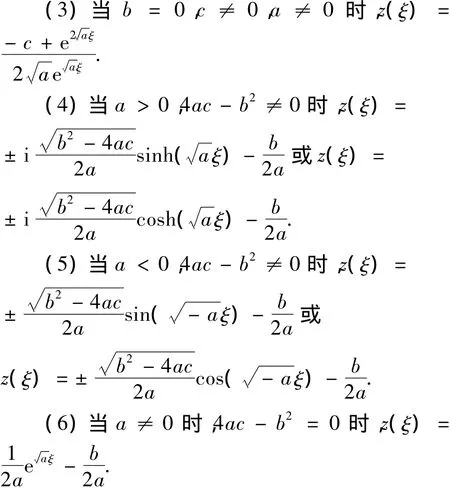
引入两个基本函数f和g,其中r为待定常数,

显然,函数f和g满足以下关系

假设常微分方程的解u(ξ)是一个关于f和g的n阶多项式,即
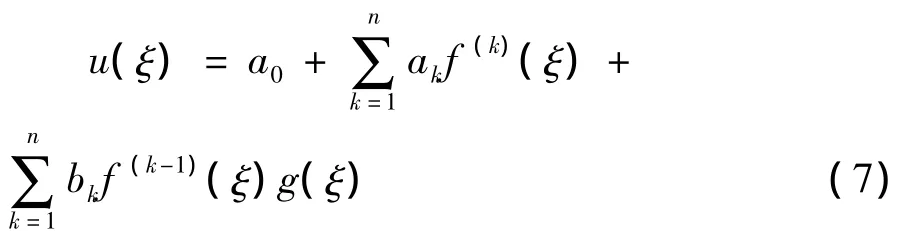
其中,系数ak和bk为待定常数,且ak+bk≠0,n由齐次平衡法来确定.
将(3)式中构造的n阶多项式代入(1)式的常微分方程,结合(6)式使得所得方程的各项中只有f和g的幂次项,合并f和g的同次幂项并取系数为零,就可以得到一个包含所有待定系数的非线性代数方程组.并对该方程组,用吴文俊消元法确定所有的待定系数,最终可得到非线性波动方程的精确行波解.
2 求精确行波解
根据以上介绍的扩展椭圆型辅助方程法,对推广的Klein-Gordon方程进行求解.(1)式对应的常微分方程为:
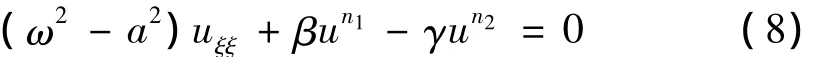
平衡方程(8)的最高阶导数项和具有支配地位的非线性项中,不妨设n1≥n2,则根据平衡原理知又n1和n1均为正整数,其中一种情形为:
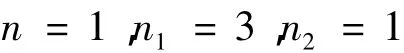
此时方程形式为:
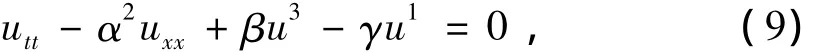
其对应的常微分方程为

因为n=1,所以上式解的形式可以写为

将(5)、(11)式代入方程(10),令多项式
fj(ξ)gk(ξ)的系数为零,可得一个包含所有待定系数的非线性代数方程组,求解得:


3 具体精确解

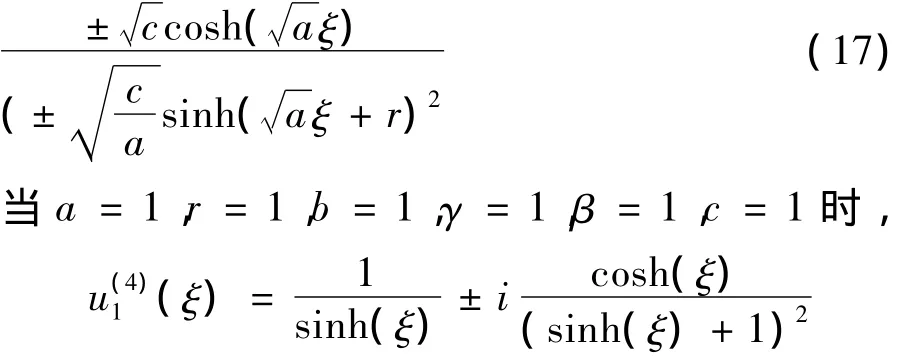
对解(17)进行数值模拟得图1.

图1 数值模拟图
4 结束语
该文通过推广的椭圆型辅助方程法,求推广的Klein-Gordon方程:utt-α2utt+βun1-γun2=0(1)的精确行波解,通过应用齐次平衡原理确定n1,n2的取值,进而对不同取值进行求解,对所求解代入特定值画图,进一步明确解的性质.椭圆型辅助方程法可以对推广的Klein-Gordon的各种形式进行求解,并且能够对f(ξ)和g(ξ)取一般形式的解进行讨论,具有一般性,该文的方法也适用于其他方程求精确行波解.
[1]张春华.再论Klein-Gordon方程解的物理意义[J].渤海学刊,1988(4).
[2]Fan Engui.Two new applications of the homogeneous balance method[J].Phys Lett A,2000,265(2000):353–357.
[3]Ismail Aslan,Yurhut Qzis.Analytic study on two nonlinear evolution equations by using the(G’/G)-expansion method[J].Comput Math Appl,2009,209:425–429.
[4]Shang Yadong,Huang Yong,Yuan Wenjun.The extended hyperbolic functions and new exact solutions to the Zakharov equations[J].Comput Math Appl,2008,200:110–122.
[5]Abdou M A.An improved generalized F-expansion method and its applications[J].Comput Math Appl,2008,214:202-208.
[6]Guo Shimin,Zhou Yubin.Auxiliary equation method for the mkdv equation with variable coefficients[J].Comput Math Appl,2010,217:1476–1483.
[7]Eric Sweet,Robert A.Van Gorder.Trigonometric and hyperbolic type solutions to a generalized Drinfel’d-Sokolov equa-tion[J].Comput Math Appl,2010,217:4147–4166.
[8]Guellal S,Cherruault Y.Application of the Decomposition Method to identify of the Distributed Parameters of an Elliptical Equation[J].Comput Math Appl,1995:51-55.
[9]沈水金.扩展的F展开法及Klein-Gordon方程的精确解[J].绍兴文理学院学报,2010,30(7).
[10]Arash Yavari,Shahram Sarkani.On applications of generalized functions to the analysis of Euler-Bernoulli beam-columns with jump discontinuities[J].International Journal of Mechanical Science,2001,43:1543–1562.
[11]Gan Zaihui,Guo Boling.Sharp threshold of global existence for the coupled nonlinear Klein-Gordon equations in three space dimensions Advance in Mathematics[J].数学进展,2009,38(6).
[12]Sun Qiang.Solving the Klein-Gordon equation by means of the homotopy analysis method[J].Comput Math Appl,2005,169:355–365.
[13]Fabio M.amorin Natali,Ademir Pastor Ferreira.Stability and Instability of periodic standing wave solutions for some Klein- Gordon equations[J].Math Anal Appl,2008,347:428–441.
[14]信春刚,王军帽,张睿,等.扩展椭圆型辅助方程法与Klein-Gordon方程新解析解[J].安徽大学学报:自然科学版,2010(3).

