关于非线性系统降维观测器设计方法的研究*

迟子孟，周 磊，王秋琳，刘 旭

(天津财经大学珠江学院)

0 引言

在文献［1］中针对具有Lipschitz条件系统的降维观测器设计问题进行了讨论，但其结果却不能应用在非Lipschitz非线性系统的观测器设计问题中，其应用具有一定的局限性.对此，该文主要研究此类非线性系统观测器存在的充分条件，并为该类非线性系统的观测器设计提供新的解决方法.

1 符号说明与研究背景

1.1 符号说明

对任意v=(η1，η2，…，ηn，y，u)，ηi∈Rn(i=1，2，…，n)，y∈Rp，u∈Rm，定义

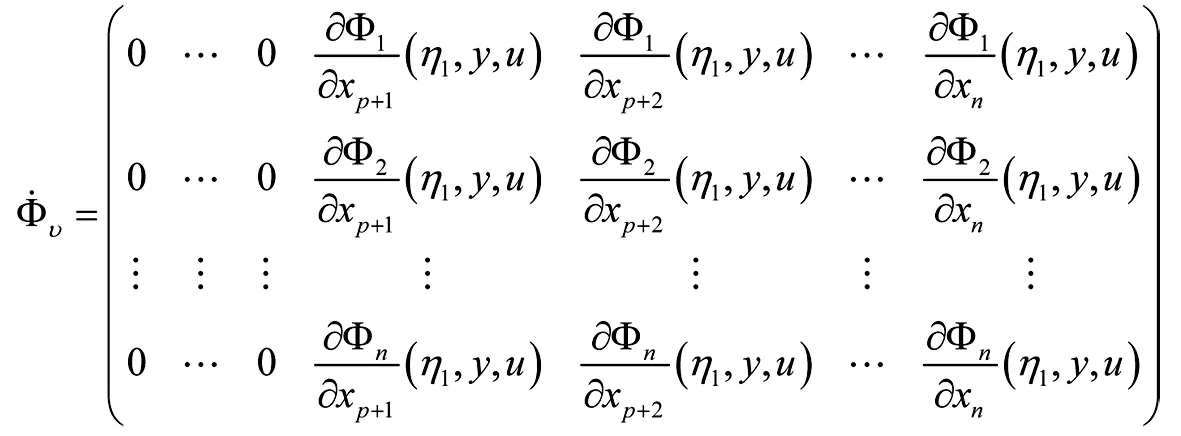
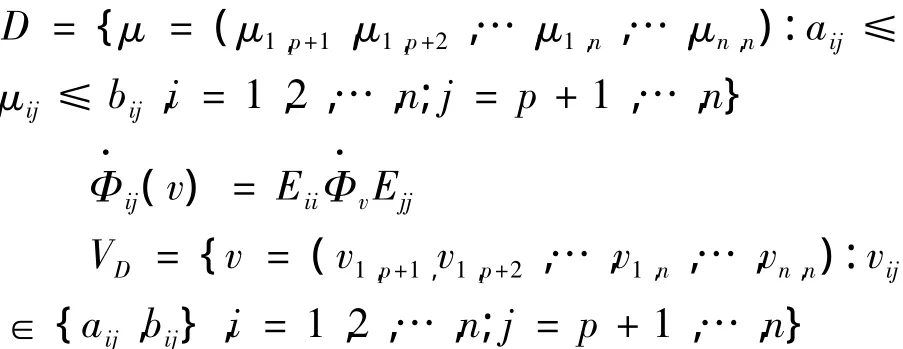
对于正定矩阵P，令

1.2 研究背景

现考虑非线性系统具有如下形式:

其中x(t)∈Rn，u(t)∈Rm，y(t)∈Rp，A∈Rn×n，C∈Rp×n.函数Φ:Rn×Rp×Rm→Rn是关于x可微的非线性部分，并且Φ(x)满足

同时具有下列形式

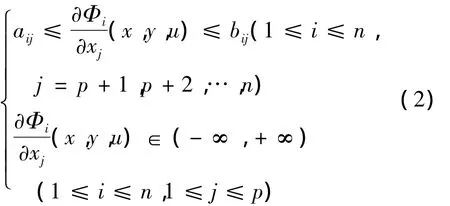
假设C是行满秩的，且(A，C)是可观测的.值得注意的是，如果存在集合{cij;i，j=1，2，…，n}和{dij;i，j=1，2，…，n}使得

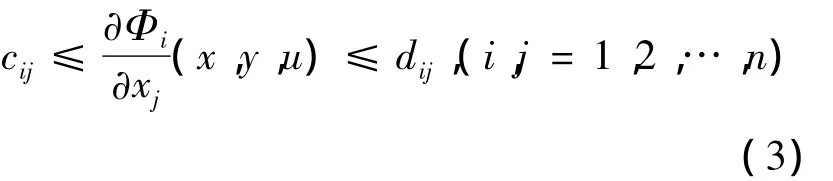
而具有该条件的系统(1)的降维观测器设计问题在文献［1］中已经讨论并也提供了相应的解决方法.可见，该文所研究的非线性系统(1)具有更为广泛的应用性.

为了方便讨论，对下面命题进行简单的论证.

命题1FP(μ)＜0(∀μ∈D⊃VD)的充要条件是FP(μ)＜0(∀v∈VD)(其中P是一个正定矩阵).

证明 由于Fp(Μ)是v∈D的一个仿射变换，利用凸集定理［2］该命题得证.

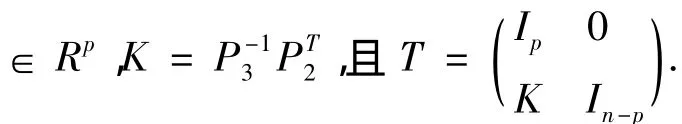
该文中，同样有

命题2 若C=(IP0)且对于=

使得

证明 记x*=(1，2，…，)T∈Rn-p，则不等式(4)左端第二行第二列的块矩阵为:

，其中z1=(x1，x2，…，xp)T=y∈Rn且z2∈Rn-p.那么，根据系统(1)，有如下结果:

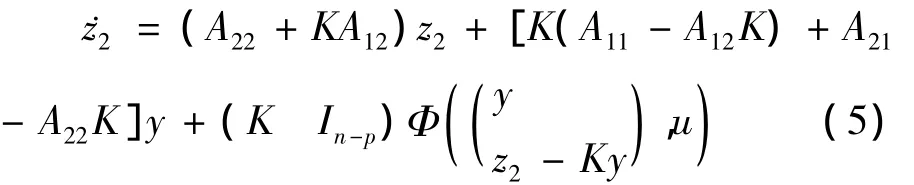
用(5)式减去文献［1］中的(12)式的第一个式子，就能得到

则其导数˙V有如下结果

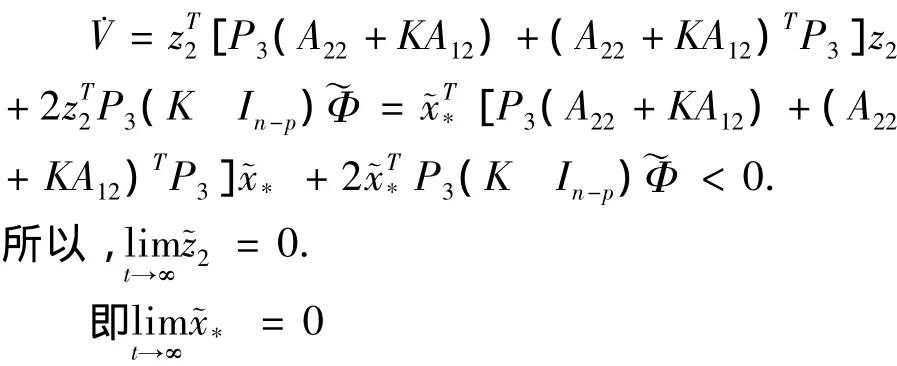
2 主要结果

结合以上的两个命题，主要给出满足条件(2)式非线性系统降维观测器设计的好方法.

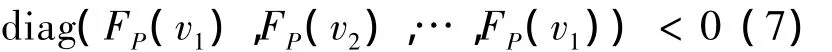
定理 如果系统(1)的非线性部分Φ(x，y，u)满足(2)式，若C=(Ip0)且存在增益矩阵K使得线性矩阵不等式存在对称正定解P，其中vi∈VD(i=1，2，…，l)，FP(v)(v∈VD)由(6)式决定.则系统(1)有如下形式的降维观测器，即

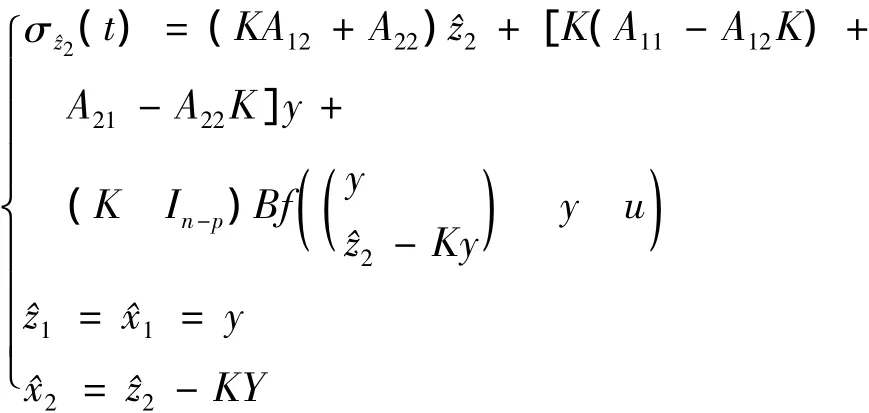
证明 对于任意v=(η1，η2，…，ηn，y，u)，

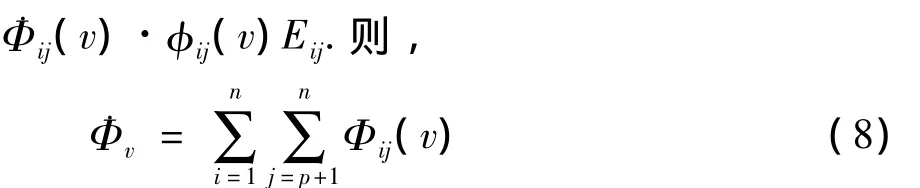
根据(8)式，对于每一个x，x∈Rn满足和正定矩阵P=(pij)n×n∈Rn×n，都存在常数向量η1，η2，…，ηn∈Co(x，)，ηi≠xi，ηi≠(i=1，2，…，n)使得下式成立

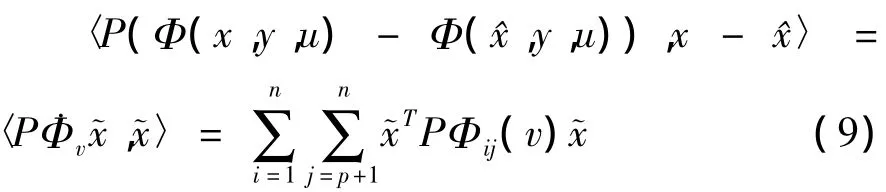
等式(9)说明

命题1和(10)意味着对于

都满足

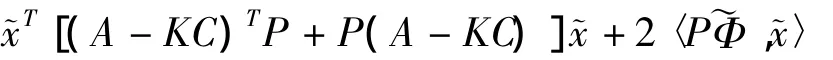
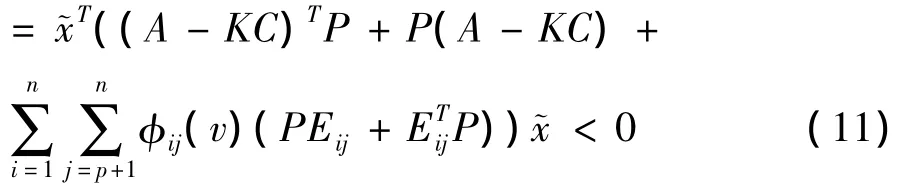
根据命题2和(11)定理得证.

［1］迟子孟，王秋琳，周磊.一类Lipschitz非线性系统降维观测器设计.哈尔滨师范大学自然科学学报，2014，4(30):1－4.

［2］Boyd S.Vandenberghe L.Convex optimization with engineering applications.Stanford University Lecture Notes，2001:101－123.

［3］董丽亚.一类非线性系统观测器设计的新方法.系统工程与电子技术，2009，1(31)153–157.

［4］Yang Fuwen.Robust state estimation for linear state delayed and measurement－ delaye systems with uncertainties［J］.Control Theory and Applications，2003，20(2):211–216.

［5］Zemouche A ，Doutayeb M ，Bara G.Observer design for non－linear systems:An approachbased on the differential mean value theorem［C］.Proc.of the 44th IEEE Conference on Decision and Cont rol and European Cont rol Conf erence，2005:6353－6358.