支持向量分类机灵敏度分析研究*

牛海军，蔡 春

(1.铁岭师范高等专科学校;2.北京联合大学)

0 引言

设有训练集T={(x1，y1)，(x2，y2)，…，(xm，ym)}∈{(X×Y)m}，其中训练输入xi∈X=Rn，训练输出yi∈Y={－1，+1}，i=1，…，m.数据挖掘中的两类分类问题即由训练集T寻找Rn上的实值函数f(x)，以便用决策函数sgnf(x)推断任意输入x相对应的类别［1］.支持向量分类机(Support Vector Classifier，SVC)是数据挖掘的新方法［2］.事实上，支持向量分类机模型中的训练输入数据xi(i=1，2，…，m)是某些特征的测定值，它只是真值的近似，使用这些近似值建立起支持向量分类机模型，数据误差必将影响所对应模型的解以及决策函数.对于已知数据误差上限的情况下，对它所引起解的误差大小能否有一个定量的估计，我们把研究这些问题的方法归于灵敏度分析方法.对于已有成熟求解理论和方法的支持向量分类机问题［3－4］，其稳定性和灵敏度分析问题也就自然成为要研究的问题.

支持向量分类机之所以能表达各种分类数据，这种强大分类功能源于把输入空间映射到高维空间，在高维空间使用线性支持向量分类机.具体的实现技巧是引入核函数，核函数恰在对偶问题中出现［5，8］，为此该文对带有核函数的优化问题进行灵敏度分析研究.参照Fiacco的一般非线性规划灵敏度分析定理［9－10］，该文建立了带有核函数的一般支持向量分类机灵敏度分析定理.

1 支持向量分类机对偶问题灵敏度分析

考虑非线性支持向量分类机原始优化问题:

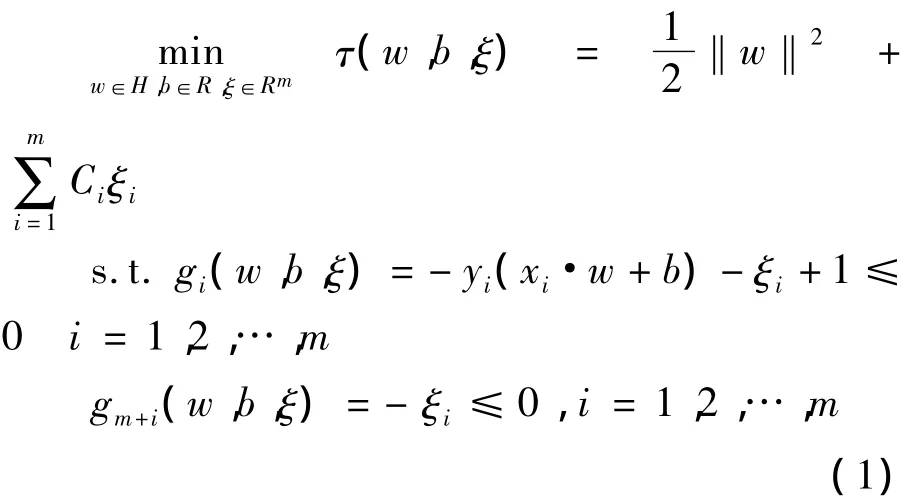
其中x=φ(x).

非线性支持向量分类机原始优化问题(1)的Wolfe对偶问题为:

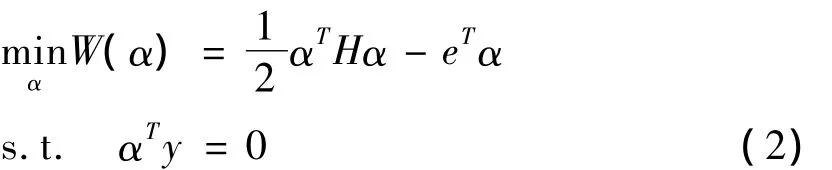
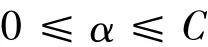
其中Hij=yiyjK(xi·xj)，e=(1，…1)T，y=(y1，y2，…，ym)T，C=(C1，C2，…，Cm)T，核函数K(xi，xj)=φ(xi)φ(xj).

为了后面灵敏度分析定理表述方便，设(w*，b*，ξ*)是问题(1)的最优解，相应于(w*，b*，ξ*)，训练数据(x1，y1)，(x2，y2)，…，(xm，ym)分为如下A、B、C三类:

A类:超平面w*·x+b*=1上yi=+1的点和超平面w*·x+b*=－1上yi=－1的点，为方便，记此类点为(x1，y1)，(x2，y2)，…，(xt，yt).

B类:开半空间w*·x+b*＞1中yi=+1的点和开半空间w*·x+b*＜－1中yi=－1的点，为方便，记此类点为(xt+1，yt+1)，(xt+2，yt+2，…，(xs，ys).

C类:开半空间w*·x+b*＜1中yi=+1的点和开半空间w*·x+b*＞－1中yi=－1的点，为方便，记此类点为(xs+1，ys+1)，(xs+2，ys+2)，…，(xm，ym).

定义了A、B、C三类点后，同时以符号A、B、C记这三类数据点的下标.由起作用约束的定义，有引理 1.1.

引理 1.1 设(w*，b*，ξ*)为(1)的最优解，则起作用约束指标集为:

在给出支持向量分类机对偶问题(2)的灵敏度分析定理前，再给出一个起作用约束梯度组线性无关引理1.2和二阶充分条件引理1.3［11］.

引理1.2 设是对偶问题(2)的最优解，若存在α*的某个分量满足0＜α*i＜Ci，则起作用约束的梯度组线性无关.

证明 对于i∈A，即i=1，2，…，t，不妨设对于;对于;对于i∈B，即i=t+1，t+2，…，s，有

对于i∈C，即i=s+1，s+2，…，m，有α*i=Ci.起作用约束梯度向量集合为ym)T、非支持向量xi对应的起作用约束的梯度、支持向量xi对应的起作用约束的梯度，它们是:

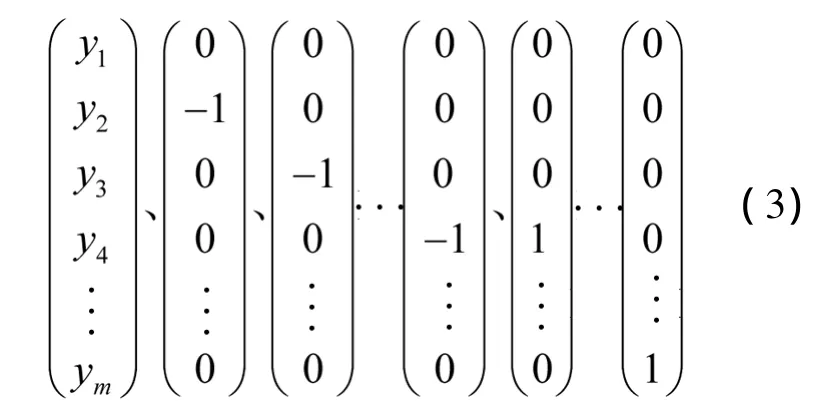
证明完毕.

引理1.3 设是对偶问题(2)的最优解，若A类点对应的向量组线性无关，则α*一定满足二阶充分条件.

有了线性无关引理1.2和二阶充分条件引理1.3，当核映射φ(x)的表达式已知时，得到优化问题(2)的灵敏度分析定理1.4.

用小写字母p表示训练输入变量，p0为已给的训练输入变量取值即训练输入数据，对于训练输入数据误差如何影响分类模型的解及决策函数，该文给出理论结果见定理1.4.

定理1.4 设α*是对偶问题(2)在p=p0的最优解，对应的拉格朗日乘子为b*，g*=，假设

(1)A 类输入x1，x2，…，xt全为支持向量，且对应的乘子αi＜Ci(i=1，…，t).

则有下面结论成立.

(1)α*为(2)的p=p0孤立最优解，并且对应的拉格朗日乘子为唯一的.

(2)存在p0的邻域N(p0)，在N(p0)上存在唯一连续可微函数y(p)=(α(p)，b(p)，g(p)，ξ(p))，使得 ①y(p0)=(α*，b*，g*，ξ*)，② 对任意的p∈N(p0)，对于问题(2)，α(p)为可行解，③起作用集保持不变;即

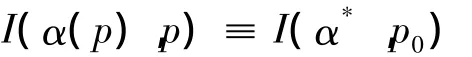
④线性无关性保持成立;⑤α(p)和g(p)，ξ(p)使严格互补性质保持成立;⑥α(p)满足二阶充分条件，相应的乘子为b(p)，g(p)，ξ(p).⑦α(p)为问题(2)的孤立最优解，b(p)，g(p)，ξ(p)为相应的唯一乘子.⑧y(p)=(α(p)，b(p)，g(p)，ξ(p))的偏导数满足

其中(4)中的矩阵:

其中L为(1)的拉格朗日乘子函数.

证明 引理1.2、引理1.3给出在本定理假设下，二阶充分条件和线性无关条件一定成立.下面证明严格互补性:

对于i∈A，i=1，2，…，t，xi为支持向量，且由假设α*i＜Ci，可得i∈A不对应起作用约束.对于i∈B，i=t+1，t+2，…，s，有起作用约束=0，乘子＞0;对于i∈C，i=s+1，s+2，…，m，有起作用约束，乘子＞0，严格互补性得证，为此可以得出定理1.4的全部结论.

2 结论

该文针对支持向量分类机对偶优化问题建立了灵敏度分析定理.通过灵敏度分析定理可以回答支持向量分类机问题解的稳定性问题.该理论研究完善了支持向量机现有的一些优化理论，为其广泛应用奠定坚实基础.

［1］邓乃扬，田英杰.数据挖掘中的新方法——支持向量分类机［M］.北京:科学出版社，2004.

［2］Vapnik V.The Nature of statistical learning theory.Springer N Y，1995.张学工译.统计学习理论的本质［M］.北京:清华大学出版社，2000.

［3］Boser B，Guyon L，Vapnik V.A training algorithm for optimal margin classifier.In fifth annual workshop on computational learning theory［M］.Baltimore，MD:ACM Press，1992:144－152.

［4］Scholkopf B，Burges C J C，Smola A J.Advances in kernel methods－ support vector learning［M］.MIT Press，Cambridge，MA，1999:327－352.

［5］向昌盛，周子英.支持向量分类机的参数选择方法研究［J］.计算机技术与发展，2010，20(9):94–97.

［6］李红英、钟波.支持向量分类机的修正核函数［J］.计算机工程与应用，2009(24):53－55.

［7］刘建伟，李双成，罗雄麟.p范数正则化支持向量机分类算法［J］.自动化学报，2012，38(1):76－87.

［8］陈圣磊，陈耿，薛晖.最小二乘支持向量机分类的稀疏化方法研究［J］.计算机工程，2011(22):146－150.

［9］Fiacco A.Sensitivity Analysis for Nonlinear Programming U-sing Penalty Methods［M］.Mathematical Programming，1976，10:287－331.

［10］刘宝光.非线性规划［M］.北京:北京理工大学出版社，1988.

［11］蔡春，刘宝光，邓乃扬.线性支持向量分类机优化问题解的二阶充分条件［J］.中国农业大学学报，2006，11(6):92－95.