非均匀钹式换能器平面阵布阵设计

彭海军，王刚，徐伟勤，吴永春



非均匀钹式换能器平面阵布阵设计

彭海军1,2，王刚2，徐伟勤1，吴永春3

(1. 海军航空工程学院青岛校区，山东青岛 266041；2. 光电控制技术重点实验室，河南洛阳 471009； 3. 中国人民解放军91055部队，浙江台州 318050)

钹式换能器尺寸小，可以大规模组阵以提高声辐射性能，但是它的工作频段低，其组阵不宜遵循传统压电阵元布阵间距的规律。为提高基阵的空间利用率而降低阵元互干扰的不利影响，提出一种非均匀平面基阵的实现方法。考虑强度非均匀因素，建立了9元基阵的阵元互辐射阻抗模型和基阵的总辐射阻抗模型，分别研究了阵元间距、工作频率和中心阵元强度对阵元互阻抗和基阵总阻抗的影响。在提高基阵总辐射效率，并保证单个阵元能有效辐射声能的原则下，给出了不同工作频率下，阵元的合适间距。为改善基阵的辐射阻抗提供了阵元间距和阵元强度两种调整办法，为研制超多阵元钹式水声设备奠定了理论基础。

钹式换能器；非均匀平面阵；互阻辐射抗；密排基阵

0 引言

钹式换能器(Cymbal)是宾夕法尼亚州立大学材料研究室(MRL)为开发新型轻型低频水下换能器而研制出的一类微型弯张换能器[1]。与传统朗之万(Langevin)型压电水声阵元相比，钹式阵元尺寸小、重量轻、剖面薄；因其独特的钹式结构，可轻松获得极低的工作频率。该型阵元接收灵敏度高，但发射响应偏低，因此必须通过组阵的方式提高发射幅压响应。对于小尺寸低频换能器，若再遵循传统Langevin型压电阵元布阵间隔的规律，那么基阵的空间利用率将极低，因此必须研究紧凑的布阵方式，且要避免阵元之间的互干扰影响基阵辐射性能[2]。

1 研究现状

由于Cymbal尺寸远小于波长，前后钹式金属帽的电压施加方式可灵活配置，这使其组阵方式和规律独具特点，包括阵元数目、声耦合效应、辐射阻抗的调节与匹配等诸多方面都有新的变化。传统形式的Langevin型压电阵元由于压电晶堆长、体积较大，基阵一般都按平面布置成圆形阵或方阵，并且基阵的阵元数目受限；对于圆柱或球形等特殊的阵型，往往使用环形压电换能器布阵；钹式水声阵元尺寸小、重量轻，所以可组成共形阵，而且可形成超多阵元的基阵，阵元的排布形式也可灵活变化。

宾州州立大学材料研究所的Newnham教授及其带领的团队对3×3钹式换能器在空气中和水中的发射和接收性能进行了系统的研究[3]。Tressler对灌封和未灌封的3×3基阵的性能进行了对比实验，结果表明：组阵后第一共振频率受到抑制，带宽变宽，并发现灌封层越厚，对发射响应的抑制越大[4]。Newnham R E等[5]对3×3钹式阵列的声负载效应进行了研究。ZHANG J等[6]计算和实验均指出了阵元互干扰的严重问题，他还制作了一个5×20的阵列，研究其水下性能，并将其安装在一个直径21 inch的铝壳上，展示了该阵列形成共形阵的潜力。文献[7]中对基阵继续进行了深入研究，制成两侧附加刚性盖板的7×7阵和8×8阵，并以7×7阵为子阵进行组合，得到2×3复合基阵。该工作详细研究了两侧附加整体盖板的技术和灌封技术，取得低至2 kHz的水下工作频率，其主要优点是可以得到较高的输出声功率。美国2007年声称已经装艇试验了两万个阵元的基阵。由于水声装置属于研究的敏感领域，所以国外组阵方面的研究成果很难获得和借鉴。组阵规律研究是开发钹式基阵过程中必须完成的工作之一。

目前国内Cymbal基阵的研究主要集中在均匀平面阵的组阵形式和性能研究上，如邢建新等[8]对3×3均匀平面基阵的辐射阻抗进行了建模和计算。唐俊等[9]制做了用钢板和导电碳纤维板夹持9个Cymbal阵元的薄型低频换能器阵，盖板统一了各阵元的辐射振速，获得低至2.5 kHz的水下共振频率。

均匀平面基阵能在一定程度上改善发射电压响应和接收电压灵敏度性能，降低Q值，并取得很低的工作频率。但是在实际应用中，尤其是大规模组阵条件下，均匀平面阵的性能必因阵元互干扰而产生不确定性，两侧附加刚性盖板的方式也限制了Cymbal的应用。本文将在前人对均匀平面基阵的研究基础上，建立3×3非均匀平面基阵的辐射阻抗模型，针对组阵的基本指标，根据阵元在声场中互辐射作用和阵元声压在远场的叠加原理，采用数值计算的方法，研究基阵的阵元间距和中心阵元强度对基阵辐射阻抗的影响，为制作基阵和验证其水下性能提供理论指导。

2 钹式基阵阻抗和阵元互阻抗分析

声辐射器的辐射阻抗决定于声压对其辐射面的作用。因为阵的每个阵元都处于阵的辐射声场之中，它面上的声压是所有阵元(包括自身在内)辐射声场的迭加。因此基阵中单个阵元的总辐射阻抗将包括自身辐射场的作用及其它阵元辐射场作用的总和。如图1所示，假设多个辐射器分布在平面上，组成平面基阵，令声源序号为，各声源的振速为。

文献[10]计算出1号阵元的总阻抗1为

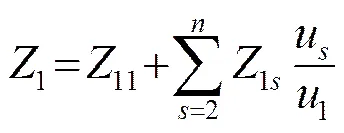
(2)

从式(2)可看出，基阵的总阻抗除了包含每个阵元的自阻抗，还包含由阵元之间互作用而增加的部分，即加号右边部分。这正是密排基阵提高辐射阻抗的原因。对于低频钹式阵列，由于工作在低频段，并且尺寸很小，所以适合于通过密排阵来提高辐射效率。

以无限大平面障板中两个活塞式换能器为例分析阵元之间的互辐射阻抗，假设阵元半径分别为和，面积为和，并且，，源强度分别为，。由文献[11]可知，钹式换能器的声辐射过程可等效为活塞式换能器，其自辐射阻抗为

(3)

活塞2对活塞1的互辐射阻抗为

所以，活塞1的总辐射阻抗为

(5)

其中，活塞1的总辐射阻和总辐射抗分别为：

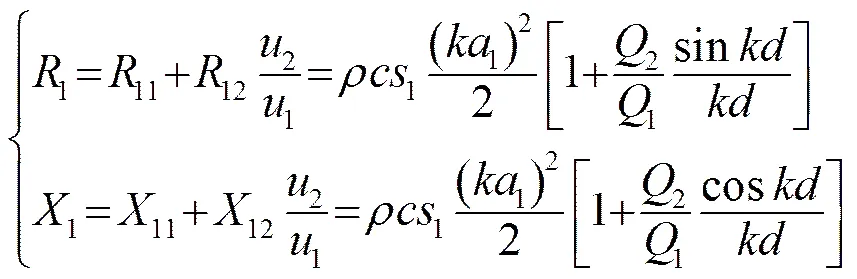
当1=2时，，

12/11、12/11与的关系曲线如图2所示。

由图2可见，由于基阵中其它阵元的互作用，使每个阵元的辐射阻抗发生很大变化。当<3时，也就是时，影响更大。当时，互阻抗的作用比自阻抗的作用小很多，阵元的互作用可以忽略。对于Cymbal一类的小尺寸低频换能器，很难达到的要求。对于密排基阵，需要考虑互阻抗对基阵辐射阻抗的影响。

3 非均匀基阵及其阵元的辐射阻抗推导

假设阵元半径为，阵元间距，阵元强度比为

根据九元阵中各阵元的位置将阵元分为A、B和C三组，对各阵元进行编号，如图3所示。

由位置对称性可知，同一组中阵元的辐射阻抗相等，即

A组中阵元的辐射阻抗为

(7)

B组中阵元的辐射阻抗为

C组中阵元的辐射阻抗为

(9)

，

，，

，，

，，，

基阵总的辐射阻抗为9个阵元的辐射阻抗之和：

(10)

因为辐射阻抗中辐射阻表示向介质中辐射的声能，所以基阵性能主要受到辐射阻的影响。A组、B组和C组中单个阵元的辐射阻分别用、和表示。将九元阵的辐射阻表示为

其中，

(12)

由上式可见，当阵元互作用不能忽略时，九元阵的总辐射阻除了包含九个阵元的自辐射阻，还包含有阵元之间相互作用而引起的互辐射阻[6]。阵的互辐射阻与阵元自辐射阻的比值为，它是阵元间距、波数以及阵元强度比的函数。必须选择合适的参数，使基阵及其阵元工作在最佳状态。

4 阵元间距和阵元强度比对辐射阻的影响

4.1 阵元间距对辐射阻的影响

考虑阵元强度无差异，即=1时，阵元间距对阵元和基阵辐射阻的影响。此时基阵的结构和响应都是均匀对称的，所以是一种均匀换能器阵。

4.1.1 阵元间距对阵元辐射阻的影响

以基本共振频率为5 kHz的钹式换能器为例，分析基阵及其阵元的阻抗特性。将=1代入三组阵元的阻抗表达式(7)、(8)和(9)，利用科学计算软件Mathematica进行数值计算，绘出、和与阵元间距的关系曲线如图4所示。阵元自辐射阻与阵元间距无关，图中纵坐标是阵元总辐射阻对阵元自辐射阻的归一化值(为、或)。

图中结果表明，随着阵元间距逐步增大，各组阵元的辐射阻迅速降低。当=13 cm时各组阵元的辐射阻第一次降低到与自辐射阻大小相近，也就是互辐射的作用变得很小。当继续增大时，阵元的辐射阻在自辐射阻的上下波动，并且波动幅度越来越小。当>30 cm时，阵元之间的互阻基本可以忽略。

从图4的曲线中可看出，A组阵元在15 cm<< 21 cm时为负值，这表示A组阵元在工作时从声场中吸收能量，这对于基阵发射声波很不利，应当避免。根据式(7)可知，使A组阵元辐射阻为负的条件是：3.25<<4.28。据此计算出在不同工作频率下，A组阵元辐射阻为负的阵元间距范围，如表1所示。

表1 使A组阵元辐射阻为负的阵元间距

其最小间距min与通常布阵所要求的阵元间距/2相当。实际应用时为了提高空间效率，布置更加紧凑，并且要保证阵元辐射阻不能为负。在选择阵元间距时，还需要考虑阵元本身直径和阵元之间灌封材料的空间。

考虑阵元间距为5 cm时，各组阵元的辐射阻随工作频率的变化情况，如图5所示：

由图5可以看出，A类阵元的辐射阻随频率的波动最大。文献[6]对9元基阵中各组阵元的法向振速进行了测量。结果显示，在共振频率附近，由于辐射阻抗增大，各阵元的法向振速降低。而A组阵元的振速降低得最大。这与本文的分析一致。A组阵元四周环绕的阵元最多，受到的互辐射作用最大，所以它的法向振速最低。由以上分析可看出，当阵元间距较小或基阵的工作频率较高时，阵元之间互辐射阻抗比较大，而且中心阵元还有可能出现辐射阻为负的情况。这主要是由于中心阵元受周围阵元的互辐射作用太大所致。

4.1.2 阵元间距对基阵辐射阻的影响

根据基阵总辐射阻抗表达式(10)，计算工作频率为5 kHz时，基阵总辐射阻随阵元间距的变化情况，如图6所示，纵坐标是总辐射阻对无辐射9元阵辐射阻的归一化值。图中虚线表示无互辐射9元阵的辐射阻。

由图6可见，当阵元间距无限小时，基阵总辐射阻接近与无辐射情况辐射阻的9倍；随着阵元间距的增大，基阵总辐射阻逐步减小；当阵元间距增加到12 cm时，总辐射阻接近无互辐射情况的总辐射阻，即阵元的互辐射作用可以忽略。如果利用阵元互阻抗来提高基阵的总辐射阻抗，则对于5 kHz工作频率的基阵，阵元间距不应大于12 cm。

当基阵工作在不同工作频率时，归一化的总辐射阻随阵元间距的变化情况如图7所示。

由图7看出，工作频率越高，基阵辐射阻随阵元间距下降越快。当阵元间距增大到z时，基阵的总辐射阻降为9个阵元的辐射阻之和。表2是z与基阵工作频率的关系。

4.2 阵元强度比对阵元和基阵辐射阻的影响

在4.1节研究中看出，依靠调整阵元间距和工作频率不能消除A组阵元工作辐射阻为负的情况。究其原因是A组阵元四周的阵元最多，受到互作用声场过强，而自身产生的声场相对来说太弱，所以在某些条件下出现被动的吸收声能的情况。本节研究通过调整A组阵元的声源强度来调节各组阵元和基阵的辐射阻抗，从而提高基阵的发射效率。

表2 基阵总辐射阻降为9阵元辐射阻之和时的阵元间距

4.2.1 阵元强度比对阵元辐射阻的影响

选取阵元间距为5 cm，工作频率为5 kHz，研究对各组阵元辐射阻的影响。当=1、1.5、2时，各组阵元对的归一化辐射阻如图8~10所示。

图中曲线显示，各组阵元在30 cm内都出现一个辐射阻最小值，此后阵元间距进一步增大时，互辐射效应变小，阵元辐射阻的波动越来越小，最后趋于恒定值。A组和B组阵元的辐射阻最小值受的影响较大。随着的增大，A的最小值上升，当=1.5时，A的最小辐射阻大于零。B组的辐射阻最小值随着的增大而降低，当=2时，最小值接近于零，进一步增大将导致B组阵元出现负的辐射阻。这表示过大时，B组阵元在某些工作频率上将变为吸收外部声能。C组的最小值变化最小，这是因为它与A组阵元的距离较大，所以互作用也小。由上面分析可知，取值在1.5到2之间时，基阵中阵元在各种阵元间距或工作频率下都不会出现辐射阻为负的情况，也就是说各阵元的辐射阻分布更加均匀。

4.2.2 阵元强度比对基阵辐射阻的影响。

当=1、1.5和2时，基阵的辐射阻如图11所示。

由图11可见，对基阵的总的辐射阻影响较小。由此看来，对基阵的调节作用主要体现在对阵元辐射阻的调节，有助于改善各阵元工作状态的均匀性。

5 结论

本文在均匀平面基阵的基础上，考虑强度非均匀因素，建立了9元基阵的阵元互辐射阻抗模型和基阵的总辐射阻抗模型，分别研究了阵元间距、工作频率和中心阵元强度对阵元互阻抗和基阵总阻抗的影响。在提高基阵总辐射效率，并且单个阵元能有效辐射声能的原则下，给出了不同工作频率下阵元的合适间距，如对于5 kHz的工作频率，阵元间距应在12 cm以内。研究结果表明：中心阵元强度变化对基阵总辐射阻抗的影响很小，但是对各阵元的辐射阻抗有显著的调节作用，当强度比值=1.5~2时，可以消除基阵中阵元辐射阻抗为负的情况。本文工作为改善基阵的辐射阻抗提供了阵元间距和阵元强度两种调整办法，为研制超多阵元钹式水声设备奠定理论基础。

[1] Zhang J D, Hughes W J, Meyer R J, et al. A Class V Flextensional Transducer: the Cymbal[J]. Ultrasonics, 1999, 37(11): 387-393.

[2] 周利生, 胡青. 水声发射换能器技术研究综述[J]. 哈尔滨工程大学学报, 2010, 31(7): 932-936.

ZHOU Lisheng, HU Qing. Development of underwater radiator technology[J]. Journal of Harbin Engineering University, 2010, 31(7): 932-936.

[3] Newnham R E, Alkoy S, Hladky A C. Underwater Flat-panel Transducer Arrays[J]. Sensors and Actuators, 2005, 124(1): 393-397.

[4] Tressler J F, Newnham R E, Hughes W J. Capped Ceramic Underwater Sound Projector：the“Cymbal”Transducer[J]. J. Acoust. Soc. Am, 1999, 105(2): 591-600.

[5] Newnham R E, Alkoy S, Hladky A C. Underwater Flat-panel Transducer Arrays[J]. Sensors and Actuators, 2005, 124(1): 393-397.

[6] Zhang J, Hughes W J, Meyer R J. Cymbal Array: A Broad Band Bound Projector[J]. Ultrasonics, 2000, 37(3): 523-529.

[7] Tressler J F, Howarth T R, Carney W L. Thin, Lightweight Electroacoustic Projector for Low Frequency Underwater Applications[J]. J. Acoust. Soc. Am, 2004, 116(3): 1536-1545.

[8] 邢建新, 蓝宇, 王智元. Cymbal基阵的布阵技术研究[J]. 仪器仪表学报, 2005, 26(3): 286-288.

XING Jianxin, LAN Yu, WANG Zhiyuan. A study on building up cymbal array[J]. Chinese Journal of scientific instrument, 2005, 26(3): 286-288.

[9] 唐俊, 秦雷, 王同庆. Cymbal单元的薄型低频宽带水声发射换能器设计[J]. 哈尔滨工程大学学报, 2010, 31(3): 281-285.

TANG Jun, QIN Lei, WANG Tongqing. Design of cymbal underwater radiator with thin profile，low frequency and broad band[J]. Journal of Harbin Engineering University, 2010, 31(3): 281-285．

[10] 何祚庸, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1980.

HE Zuoyong, ZHAO Yufang. Base theory of sound[M]. Beijing: National Defense Industry Press, 1980.

[11] 彭海军. 钹式水声基阵阵元设计与等效性能研究[D]. 武汉: 海军工程大学, 2010.

PENG Haijun. Element design and equal performance of underwater cymbal array[D]. Wuhan: Naval University of Engineering, 2010.

Design of nonuniform planar cymbal array

PENG Hai-jun1,2, WANG Gang2, XU Wei-qin1, WU Yong-chun3

(1.Qingdao Branch, Naval Aeronautical Eng. Institute, Qingdao 266041, Shandong, China;2.Science and Technology on Electro-optic Control Laboratory, Luoyang471009, He’nan, China; 3.The PLA 91055 Army, Taizhou 318050, Zhejiang, China)

The size of cymbal is so small that it needs to be integrated into an array to enhance sound transmitting performance. But its working frequency is very low, and the spacing of elements can’t obey traditional law. In order to maximize the spaceavailability and minimize the interference between elements, a nonuniform planar cymbal array is considered.The cymbal array and its 9 elements’ radiation impedance models are developed and calculated. The effects of elements’ spacing, working frequency and center element’s strength on mutual radiation and the impedance of the array are studied. Proper spacing at different frequencies to insure maximal radiation efficiency is calculated. This article provides two approaches to optimize the array radiation impedance: the elements’ spacing and strength. Results are useful for underwater sound equipments with massive cymbal array.

cymbal array; nonuniform planar array;mutual radiation impedance; compact arranged array

TP212 TB534.2

A

1000-3630(2015)-01-0096-06

10.16300/j.cnki.1000-3630.2015.01.018

2013-11-08;

2014-02-01

光电控制技术重点实验室和航空科学基金联合资助项目(20115185003)

彭海军(1980－), 男, 湖南汨罗人, 博士, 研究方向为航空电子系统。

彭海军, E-mail: penghj0383@sina.com