免疫算法在分数阶Fourier变换域极值优化中的应用

刘清宇，卫红凯

免疫算法在分数阶Fourier变换域极值优化中的应用

刘清宇1，卫红凯2

(1. 海军装备研究院，北京100161；2. 海军工程大学，湖北武汉430033)

利用线性调频(Linear Frequency Modulation, LFM)信号在分数阶Fourier域上的聚焦性，通过搜索可实现LFM信号的检测和参数估计。通常采用步进式搜索法，效率低下。为了克服该缺点，通过对分数阶Fourier域优化问题的研究，将免疫算法引入到分数阶Fourier变换极值搜索中。仿真结果表明：该方法优于传统的步进式搜索法。

免疫算法；分数阶Fourier变换；极值优化

0 引言

传统的傅里叶变换(Fourier Transform, FFT)采用正弦基，适合于处理平稳信号。但实际中，许多信号的统计特性往往随时间变化，表现出非平稳特性。为了描述非平稳信号的时变特征，需要寻求新的时频分析工具，分数阶傅里叶变换(Fractional Fourier Transform, FRFT)[1-3]是基于此出现的一种信号处理新方法。FRFT采用线性调频基，特别适合于处理Chirp类信号。线性调频信号在特定的分数阶Fourier域上能够实现聚焦，称为LFM信号在分数阶Fourier域上具有聚焦性。常用此聚焦特性检测在通信、雷达、声呐等领域中应用广泛的LFM信号。

目前，常用的LFM信号检测方法是步进法[4-6]。即设定参数步长，在分数阶Fourier域平面对LFM信号进行二维步进搜索。但步进式搜索算法效率低下，尤其是当精度要求高时，更是如此。通常离散采样信号经FRFT后，除了对应LFM信号的最大峰值外，在分数阶Fourier域平面还会出现多个局部峰值。因此，分数阶Fourier域的极值搜索本质上是全局寻优问题。免疫算法[7-10]是近年来出现的一种仿生类全局优化算法，该法具有所需函数信息少、全局性和鲁棒性好等优点。因此，本文将免疫算法引入到FRFT中，提出了一种基于免疫算法的分数阶Fourier域极值优化算法，从而实现LFM信号的检测。通过仿真实例，验证了本文所提方法的效率优于传统的步进式搜索方法。

1 分数阶Fourier域优化问题描述

分数阶Fourier变换由Namias于1980年提出[1]，可理解为信号在时频平面的旋转算子。其定义如下：

实际中，信号由离散化采样值表示。因此，需要将连续分数阶Fourier变换离散化，本文采用Ozaktas[3]提出的离散化快速算法，即：

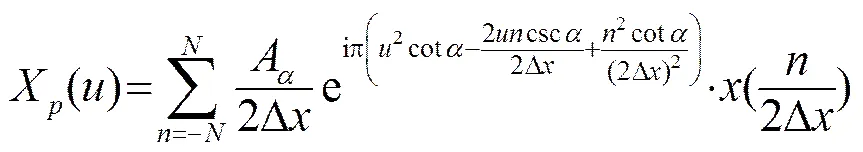
分数阶Fourier域二维极值搜索问题可描述为：在分数阶Fourier域二维平面内，寻找合适的，使得分数阶Fourier域目标函数达到最大，其数学表达式为

(3)

由式(2)和(3)可知，分数阶Fourier域目标函数形式复杂，为多个二维复杂指数函数的非线性叠加。这使得信号经FRFT后，目标函数呈现出非凸、多峰等特性。进一步增加了分数阶Fourier域二维寻优的难度。

2 免疫算法

生物免疫系统是一种复杂的自适应系统，通过学习对“自己”和“非己”抗原的分类识别，形成对应的防御机制，以对抗外部病原体入侵，使系统损害最小化。免疫算法(Immune Algorithm, IA)[7-10]就是研究人员基于免疫原理，提出的一种模拟生物免疫系统功能的智能寻优算法。由于免疫算法具有生物免疫系统的多样性、鲁棒性、并行性、智能性等特点，在优化求解、鲁棒控制、神经网络等方面得到了广泛应用。

IA对最优解的搜索类似于免疫体对抗原识别和应答的进化学习过程。IA的每个解称之为一个抗体个体，每组抗体的集合称之为抗体群，抗原对应具体的优化问题，抗体的适应度表征抗体的亲和度。在免疫应答过程中，亲和度高的抗体，更容易被选择作为优质抗体进行克隆、变异、抑制、刷新等进化操作，而亲和度低的抗体在进化过程中将被淘汰和更新。在最优化问题中，优质抗体通过变异操作，产生有潜力的新抗体，实现局部搜索。通过克隆抑制亲和度低的变异抗体，保留亲和度高的变异抗体进入抗体群。为保持抗体多样性，在抗体群中加入随机抗体实现抗体群刷新。子代抗体对应更接近最优值的解，IA即是通过各子代抗体的迭代，来找到最优解。

IA的计算步骤如下：

(1) 根据待优化问题(抗原)，确定解空间，在解空间内随机产生初始解(抗体群)，并对初始解进行二进制编码。

(2) 以目标函数值作为适应度函数，并计算各抗体的适应度(亲和度)和浓度。

(3) 是否满足终止条件，若满足，则停止运算，以当前解作为最优解输出，否则继续以下步骤。

(4) 根据抗体亲和度和浓度，选择优质抗体进行克隆、变异和克隆抑制。

(5) 以随机生成的新抗体更新抗体群中亲和度较低的抗体，实现抗体刷新，并转入步骤(2)。

算法流程如图1所示。

3 仿真实例

下面通过几个实例来说明免疫算法的良好性能。

表1 0.15s脉宽时直接法与免疫算法性能比较

表2 0.3s脉宽时直接法与免疫算法性能比较

表3 0.5s脉宽时直接法与免疫算法性能比较

表4 0.9s脉宽时直接法与免疫算法性能比较

表5 1.2s脉宽时直接法与免疫算法性能比较

表1~5为不同脉冲宽度下，直接法与免疫算法性能比较，从表中可以看出，随着脉宽的增大，免疫算法的优势越来越明显。各表中估计值和理论值有偏差，这是由于信号的离散化采样及噪声的影响导致的。直接法的计算时间和估计精度与步长有关，随着步长的增加，尽管其估计精度提高，但以牺牲运算效率为代价。免疫算法不仅耗时少于直接法，且其精度高。

4 结论

LFM信号经分数阶Fourier变换后，在分数阶Fourier域上会形成峰值。通常，对该峰值的搜索多是通过步进式搜索法进行。本文将免疫算法引入到分数阶Fourier变换极值搜索中，相比于传统步进法，本文方法精度高、收敛速度快。通过仿真实例验证了本文方法的性能。

当然，由于水声信道的复杂性，例如水声信道是一种多径信道，那么在这种情况下，本文的方法是否有效，有待于今后在实践中去验证。

[1] V Namias. The fractional order Fourier transform and its application to quantum mechanics[J]. J. Inst. Math. Appl., 1980: 25(3): 241-265.

[2] Ozaktas H M, Mendlovic D. Fractional Fourier transforms and their optical implementation[J]. J. Opt. Sco. AM. A., 1993: 10(12): 2522-2531.

[3] Ozaktas H M, Arikan O, Kutay A. Digital Computation of the Fractional Fourier Transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2141-2150.

[4] 张淑宁, 赵惠昌, 吴兵. 基于分数阶傅立叶变换的伪码体制引信线性调频干扰抑制技术[J]. 兵工学报, 2006, 27(1): 32-36.

ZHANG Shuning, ZHAO Huichang, WU Bing. LFM interference excision technique in pseudo-random code fuse based on fractional Fourier transform[J]. Acta Armamentarii, 2006, 27(1): 32-36.

[5] 赵兆, 是湘全. 一种基于分数阶Fourier变换的雷达运动目标检测算法[J]. 电讯技术, 2007, 47(4): 95-98.

ZHAO Zhao, SHI Xiangquan. A moving targets detection algorithm based fractional Fourier transform(FRFT)[J]. Telecommunication Engineering, 2007, 47(4): 95-98.

[6] 董永强, 陶然, 周思永, 等. 含未知参数的多分量Chirp信号的分数阶傅里叶分析[J]. 北京理工大学学报, 1999, 19(5): 612-616.

DONG Yongqiang, TAO Ran, ZHOU Siyong, et al. The fractional Fourier analysis of multicomponent chirp signals with unknown parameters[J]. Journal of Beijing institute of technology, 1999, 19(5): 612-616.

[7] Castro D, Zuben V. Learning and optimization using the clonal selection principle[J]. IEEE Trans on Evolutionary Computation, 2002, 6(3): 239-251.

[8] 蔡自兴, 龚涛. 免疫算法研究的进展[J]. 控制与决策, 2004, 19(8): 841-846.

CAI Zixing, GONG Tao. Advance in research on immune algorithms[J]. Control and Decision, 2004, 19(8): 841-846.

[9] 孙宁, 彭喜原, 乔立岩. 引导型免疫算法研究[J]. 电子学报, 2005, 33(12A): 2401-2405.

SUN Ning, PENG Xiyuan, QIAO Liyan. Study on guiding immune algorithm[J]. Acta Electronica Sinica, 2005, 33(12A): 2401-2405.

[10] 闫家尚, 杜江. 具有可变阈值的免疫算法[J]. 计算机工程与设计, 2009, 30(14): 3281-3287.

YAN Jiashang, DU Jiang. An immunology algorithm with variable threshold[J]. Computer Engineering and Design, 2009, 30(14): 3281-3287.

Application of immune algorithm to extremum searching in the fractional Fourier domain

LIU Qing-yu1, WEI Hong-kai2

(1. Naval Academy of Armament,Beijing 100161, China; 2.Navy Engineering University, Wuhan 430033,Hubei,China)

Based on the concentrated characteristics of linear frequency modulation (LFM) signal in the fractional Fourier domain, the detection and parameter estimation of LFM signal are usually realized by step-based searching method for extremum searching in the fractional Fourier domain. In order to resolve the disadvantage of low efficiency of the step-based searching method, Immune Algorithm is introduced to the fractional Fourier transform for extremum searching with the study of fractional Fourier optimization. Simulation results show that the performance of the Immune algorithm is better than that of the traditional step-based method.

immune algorithm; fractional Fourier transform; extremum searching

TB566

A

1000-3630(2015)-01-0075-04

10.16300/j.cnki.1000-3630.2015.01.014

2014-11-11;

2015-01-13

刘清宇(1968－), 男, 河南商丘人, 研究员, 研究方向为水声数据分析。

卫红凯, E-mail:whk200605@163.com