一种基于相关积分的互谱WVD目标方位估计方法

孙向前，范展，李晴

一种基于相关积分的互谱WVD目标方位估计方法

孙向前1，范展2，李晴2

(1. 广东湛江91388部队，广东湛江 524022；2. 哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨 150001)

针对水下高速运动目标的被动跟踪问题，将魏格纳-威尔分布(Wigner-Ville Distribution, WVD)算法与互谱法相结合，构建了一种矢量信号处理框架下的目标方位估计方法——基于相关积分的互谱WVD算法。该算法利用了矢量水听器声压通道与振速通道信号的相关特性，首先通过计算两者的互相关函数来提取目标信号的特征信息，然后通过短时积分与傅里叶变换将互相关函数从时域转换到频域，最后在频域提取信号的特征参量，并进行方位估计。仿真研究表明，当目标处于远距离且低速运动时，所提算法的方位估计性能与互谱声强法基本一致；而当目标处于近距离且高速运动时，算法的方位估计性能大大优于互谱声强法。

矢量信号处理；相关积分；互谱WVD；方位估计

0 引言

近年来，随着水中兵器机动性能的不断提高，对水下高速运动目标的定位与跟踪提出了更高的要求[1]。由于现有的水下运动目标跟踪系统大多采用主动或合作的工作模式[2]，它们通常只能适用于一些特定的应用场合，这大大限制了其应用与发展。相比之下，被动模式的水下目标跟踪系统具有更广泛的应用空间，因而也受到了越来越多的关注。另一方面，矢量水听器技术经过10多年快速发展之后，显示出越来越多的优势[3-5]，这为我们解决水声问题提供了新的思路和方法。本文以矢量水听器在水下工作平台上的应用为背景，研究水下高速运动目标的被动定位算法。

被动模式的目标跟踪系统直接利用运动目标辐射的噪声对其进行定位。对于水下高速运动的目标，其辐射的噪声中通常包含轴频、叶频以及一系列倍频组成的线谱噪声，这些特征噪声可用来对运动目标进行检测与识别。但是，受目标高速运动的影响，这些线谱噪声的频谱特性会发生多普勒扩展，这对于噪声的检测与参数估计都是非常不利的。为了降低多普勒效应带来的负面影响，需要研究抗多普勒扩展的有效方法。

本文将魏格纳-威尔分布(Wigner-Ville Distribution, WVD)与互谱法[6]有机结合，构建了一种适用于水下高速运动目标方位估计的新算法——基于相关积分的互谱WVD算法。该算法能够有效消除多普勒效应带来的负面影响，提高方位估计的性能。同时，还针对不同运动速度、不同距离和不同信噪比条件进行了仿真研究，仿真结果表明该方法对线谱方位估计及连续谱方位估计均有效。

1 WVD算法原理

WVD变换具有良好的时频聚集特性，是分析非平稳时变信号的重要工具。解析信号的WVD变换定义为

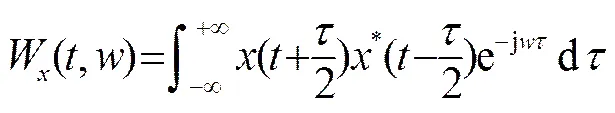
(2)

2 互谱WVD算法基本原理

在矢量信号处理中，互谱法是一种有效的方位估计算法。但是，如果存在由多普勒效应而导致的信号模型失配，线谱信号的能量有可能得不到有效地聚集，使互谱法有可能失效。本文算法利用矢量水听器振速通道与声压通道信号的相关性，将WVD算法与互谱法相结合，来提取目标信号的特征信息，以提高算法对多普勒效应的鲁棒性。下面介绍这种算法。

在目标运动的条件下，矢量水听器三个通道接收到的信号可以表示为

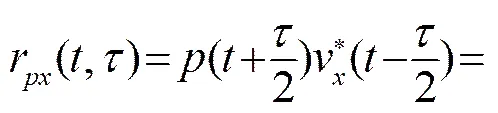
(4)

为了简化起见，将用下标符号表示，用下标符号表示，同时定义函数、和具有如下形式：

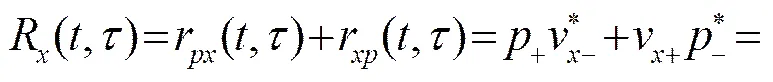
(5)

(7)

对式(5)和式(6)进行适当整理可得：

(9)

3 方位估计方法的实现

第一步：按照式(5)、式(6)和式(7)分别计算相关函数、和；

(11)

(12)

第三步：对式(10)、式(11)和式(12)的运算结果作傅氏变换得到它们的频谱、和，然后根据这三个频谱函数求出它们的互谱强度：

(14)

第四步：利用以上互谱强度估计目标方位：

4 仿真分析

本节中对互谱WVD算法的方位估计精度进行仿真分析。文献[3]推导了方位估计的克拉美罗界，

式中：为信号有效带宽；为积分时间；是信号的谱级信噪比；为矢量水听器测量模型系数。对于线谱分量，取1 Hz。本文考察的是二维模型，取0.5。

4.1 线谱方位估计仿真验证

首先针对线谱情况，为了检验互谱WVD算法的性能，针对不同距离、不同速度和不同信噪比下的线谱方位估计进行了仿真验证，并将估计精度与互谱声强法和文献[3]推导的克拉美罗界进行比较。

实验一：目标静止情况下的性能分析

假设目标发射的是单频线谱信号，信号频率为3000 Hz，噪声带宽为4000 Hz，观测时间为1 s，相关积分时间为0.1 s，目标初始位置设为(100,100)。信号的谱级信噪比变化范围为10~36 dB，每种信噪比下进行1000次实验，然后统计出方位估计标准差，统计结果见图1。

从图1中可以看出，在高信噪比时，两种方法的估计精度基本一致，而在低信噪比时，互谱声强法优于互谱WVD法。这主要与WVD运算有关，当接收信号中包含多个分量时，WVD算法容易产生交叉项干扰，这些交叉项干扰从一定程度上降低了信号的信噪比，并且在低信噪比时尤为显著。从图1中还能看到，当信号的谱级信噪比为29.14 dB时，其方位估计精度达到1°。

实验二：针对不同距离与不同运动速度情况下的方位估计性能分析

在本实验中，分四种场景研究互谱WVD算法的方位估计性能。

(1) 将目标初始位置设为(100, 100)，考察目标分别以15、25和50 m/s运动的情况，其运动方向与轴正向的夹角为135°，三种情况下的相关积分时间分别设为0.1、0.08和0.04 s。得到的仿真结果分别见图2、图3和图4。从图中可以看出，随着目标运动速度的提高，多普勒效应带来的负面影响逐渐加剧，导致互谱声强法的方位估计性能也逐渐降低，由此可以看出，多普勒效应对互谱声强法具有较大的影响。对于本文提出的互谱WVD算法，它能够将线谱分量在频率轴上有效聚集，因此获得了更好的方位估计效果。

(2) 假设目标起始点位于(300, 300)，目标运动速度设置同上，另外，三种运动速度对应的相关积分时间分别设为0.1、0.09和0.05 s，仿真结果见图5、图6和图7。

从图5与图6可以看出，当目标运动速度分别设为15 m/s和25 m/s时，两种算法得到的方位估计性能基本一致，这主要因为随着目标相对距离的增大，多普勒效应逐渐减弱，因此对算法的影响也相应地减弱。但是，从图7可以看出，当目标运动速度变为50 m/s时，互谱声强法依然受到了较大的影响，此时，互谱WVD算法的估计性能明显优于互谱声强法。

(3) 将目标初始位置设为(500, 500)，目标运动速度设置同上，三种速度对应的相关积分时间分别设为0.12、0.1和0.1 s，得到方位估计结果见图8、图9和图10。

(4) 将目标初始位置设为(1000, 1000)，三种运动速度对应的相关积分时间分别设为0.12、0.1和0.1 s，仿真结果见图11、图12和图13。

以上针对不同距离、不同速度下的目标运动过程进行的仿真研究表明：

(1) 当目标处于近距离且高速运动情况下，目标运动带来的多普勒效应对互谱声强法的方位估计性能带来了较大的负面影响，而本文提出的互谱WVD算法能够将线谱分量在频率轴上有效聚集，有效消除了多普勒效应带来的影响，其方位估计性能明显优于互谱声强法；

(2) 随着目标相对距离的增加，目标运动带来的多普勒效应逐渐减弱，对目标方位估计带来的影响也相应减弱，因此在低速度远距离情况下，两种算法得到的方位估计性能比较接近。

4.2 连续谱方位估计仿真验证

采用互谱法对连续谱信号进行处理，方位估计精度与各个通道信号的相关性有很大关系。由矢量水听器的工作原理可知，无论目标运动产生的多普勒效应有多大，各个通道受多普勒的影响是完全相同的，其所接收的信号也是完全相关的。所以多普勒效应对连续谱信号的方位估计影响很小。此时，仅需考虑目标位置变化对方位估计的影响。

下面首先分析目标静止的情况。假设选用的环境噪声与目标信号的带宽均为4000 Hz，积分时间设为1 s，目标初始方位设为45°，信号的谱级信噪比变化范围设为1~28 dB。分别采用两种方法对目标方位进行估计，每种信噪比下统计1000次，得到的结果见图14。

从图中可以看出，两种方法在目标静止时的方位估计精度基本一致。假设目标初始位置坐标为(100, 100)，运动速度为50 m/s，其运动方向与轴正向的夹角为135°，得到的结果见图15。

比较图14和图15不难发现，两种条件下的估计精度基本一致。这说明基于相关积分的互谱WVD算法对连续谱方位估计依然是有效的。

5 结语

本文介绍了一种适用于目标方位估计的新算法——互谱WVD算法。针对不同运动速度、不同距离和不同信噪比条件下的实例进行仿真研究，并将该算法与互谱声强法以及克拉美罗界进行比较。仿真结果表明，对于线谱方位估计而言，当目标处于远距离且低速运动时，两种算法的方位估计性能基本一致；而当目标处于近距离且高速运动时，互谱WVD算法的方位估计性能大大优于互谱声强法。同时，在连续谱方位估计上，两种算法的性能比较接近。

[1] 范展. 目标高速运动对矢量信号处理的影响及匹配技术研究[D]. 哈尔滨: 哈尔滨工程大学硕士学位论文, 2009.

FAN Zhan. The influence and fitting research of target’s high velocity to the vector signal processing[D]. Master dissertation of Harbin: Harbin Engineering University, 2009.

[2] 王燕, 岳剑平, 冯海泓. 双基阵纯方位目标运动分析研究[J]. 声学学报, 2001, 26(5): 405-409.

WANG Yan, YUE Jianping, FENG Haihong. Study on bearings-only target motion analysis based on association of dual arrays[J]. Acta Acustica, 2001, 26(5): 405-409.

[3] 王德俊. 矢量声场与矢量信号处理理论研究[D]. 哈尔滨: 哈尔滨工程大学博士学位论文, 2004.

WANG Dejun. Theoretical studies on vector acoustic field and vector signal processing[D]. Harbin: Doctoral dissertation of Harbin Engineering University, 2004.

[4] 姚直象, 惠俊英, 殷敬伟, 等. 基于单矢量水听器四种方位估计方法[J]. 海洋工程, 2006, 24(1): 122-127.

YAO Zhixiang, HUI Juying, YIN Jingwei, et al. Four approaches to DOA estimation based on a single vector hydrophone[J]. The Ocean Engineering, 2006, 24(1): 122-127.

[5] 惠俊英, 惠娟. 矢量声信号处理基础[M]. 北京: 国防工业出版社, 2009.

HUI Junying, HUI Juan. Vector acoustic signal processing foundation[M]. Beijing: National Defense Industry Press, 2009.

[6] 冯海泓, 梁国龙, 惠俊英. 目标方位的声压、振速联合估计[J]. 声学学报, 2000, 25(6): 516-520.

FENG Haihong, LIANG Guolong, HUI Junying. The direction estimation using combined sensor with pressure and particle velocity[J]. Acta Acustica, 2000,25(6): 516-520.

A method of target DOA estimation based on correlation integral and cross spectrum WVD

SUN Xiang-qian1, FAN Zhan2, LI Qing2

(1.Unit 91388,PLA, Zhanjiang 524022, Guangdong, China;2. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

Considering the problem of passively tracking for high speed underwater moving targets, a method of target DOA estimation based on instantaneous correlation integral and cross spectrum WVD is proposed in the framework of vector signal processing. The proposed algorithm utilizes the correlation features of the vector sensor. The basic idea is firstly to compute the instantaneous correlation of acoustic signals received by vector hydrophone;then to obtain the spectrum through short time integral of the correlation and Fourier Transform; and finally to estimate the direction of target by cross spectrum acoustic intensity method. Simulation results show that the performance of the proposed algorithm is in accordance with that of cross spectrum acoustic intensity algorithm when the target is at long distance and at low speed; however, the former performs remarkably better than the latter when the target is at short distance and at high speed.

vector signal processing; correlation integral; cross spectrum WVD; DOA estimation

TN556

A

1000-3630(2014)-06-0023-06

10.16300/j.cnki.1000-3630.2015.01.005

2013-11-03;

2014-02-02

国家自然科学基金资助项目(51279043, 61201411)、国家“863计划”资助项目(2013AA09A503)、水声技术重点实验室基金资助项目(9140C200802110C2001)、海军装备预研资助项目(1011204030104)。

孙向前(1968－), 男, 工程师, 研究方向为水声测控总体技术。

范展, E-mail: fanzhan@hrbeu.edu.cn