抓住契机，培养学生的思维能力

张莉

摘 要：基础教育课程改革的具体目标是注重知识传授的过程，强调形成积极主动的学习态度，在获得基础知识和基本技能的过程中学会学习，提高能力。所以教师要改变思维方式，调动学生的积极性，抓住契机，提升学生的思维品质。

关键词：数学 思维能力 契机

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2015）08B-0074-02

数学作为一门基础学科，重要性不仅体现在数学知识的掌握和应用上，也反映在学生的思维品质上。所以数学课堂不仅是传授知识，也教会学生分析问题、解决问题，培养学生的思维能力。这就要求教师对授课内容有深刻的认识，对学生有充分的了解，抓住课堂每个契机，激发学生的学习热情，不断提升思维品质。

一、借题发挥引其思

数学课堂有很多时间是习题教学，很多教师喜欢讲一道例题，马上做一个练习。表面上教师讲得清楚明白，学生的当堂反馈效果较好，实际上很多学生只是被动模仿，并没有养成思考的习惯，久而久之，学习热情减退，思维能力下降，成绩不尽理想。如果教师能够精心准备，选出一些具有代表性的习题，或者找出题目之间的联系，或者对题目进行“再创造”，或者进行一题多解，层层递进，从不同的角度刺激学生的思维，培养学生的探究能力，可以达到事半功倍的目的。我听过一节同行的习题评讲课，题目如下：

如图，直线 l过正方形 ABCD 的顶点 B ， 点A、C 到直线l的距离分别是 1 和 2 ， 则正方形的边长是？

学生通过构造全等形很快求出了边长，洋洋得意之时，老师对这道题进行了更深一层的挖掘，提出如下问题：

1.如图1，你有办法解决点D到直线 l的距离DH的长吗？

∵∠ADG=∠HBG，tan∠HBG= ，∴G为AB的中点，

∴GH= AE= ，DG= ，即DH=3.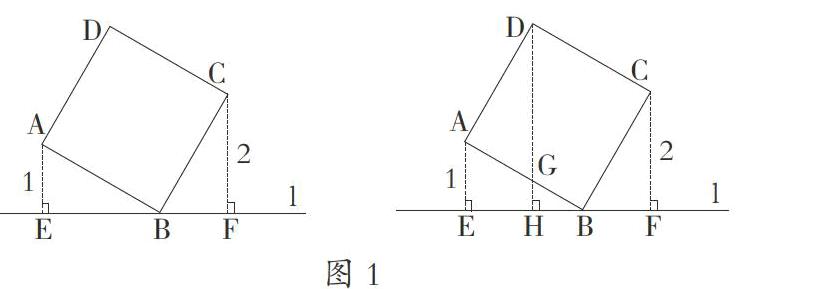

2.若我将正方形进行旋转，如图2，令AE=CF，且AB= BC.则AE、CF、DH的长可否求出？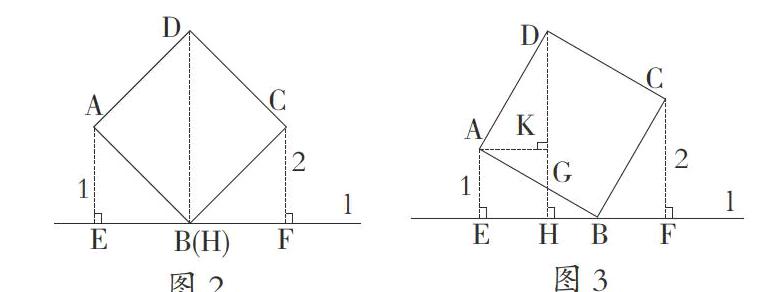

3.根据以上的计算结果，你能找到AE、CF、DH三条线段的关系吗？（AE+CF=DH）这个关系具有一般性吗？利用图3进行证明。

根据学生的解题情况，教师温故了“截长补短”的证明方法，作AK⊥DH于点K，易证：AE=KH，CF=DK，从而结论成立。

学生经过一系列的探索，得到了一般的规律，如图4。教师又高瞻远瞩，提出新问题：在刚才的问题中，直线l始终经过点B，若是它不经过任何一个顶点，结果又如何？易证△ADM≌△CBN，得DM=BN，即点A、D到直线 l的距离之和与点B、C到直线 l的距离之和相等。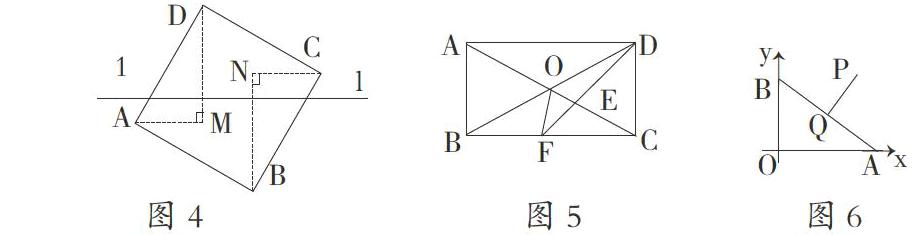

教师通过对这道中考题的引申，拓宽了学生的知识面，同时锻炼了学生的观察能力、归纳能力和类比思想；学生在自我探索的过程中体会到数学题的奇妙，体验了成功的喜悦。

二、指点迷津导其行

课堂上，教师的主要工作就是指点迷津。我觉得这个“指点”突出两个意思：一是指导作用。教师是课堂的引导者，是用简明扼要的语言引导学生思考，而不是灌输，不是把问题一步不落地讲解。二是点到为止。教师指点的面不要太宽，不能追求面面俱到，要有针对性，如学生的易错点、困惑点、知识的重难点或是可以培养学生创新能力、发散思维的点。当然指点的时机要掌握得恰到好处，过晚会失去指点的意义，过早则会影响学生的思考。

如图5，在矩形ABCD中，DE平分∠ADC交AC于E，交BC于F，∠BDF=15°。

（1）证明：CO=CF；（2）求∠COF的度数。

解法分析： DE平分∠ADC，能得到∠ADF=∠CDF，从而得到△CDF是等腰直角三角形，所以有CF=CD。因为∠BDF=15°，所以∠BDC=60°，从而出现了等边三角形，有CO=CD。综合上述结论，得到CO=CF。在这个结论下，再求底角∠COF的度数就很简单了。

学生在解决这道题时往往先考虑证明∠COF=∠CFO，再通过等角对等边证明CO=CF，从而陷入困境。在学生深思熟虑以后，教师只要点拨一下：不能直接证明相等，是不是可以尝试间接证法？看看能不能找到中间量？这样的点拨能让学生有“柳暗花明又一村”的感觉。

课堂点拨是一门精妙的启发艺术。“点”，即点出问题的实质，击中解题的要害；“拨”就是拨开遮掩问题的雾障，展现解题方法。巧妙机智的点拨，不仅能引领学生思考问题的方向，也能让学生在解决问题的过程中，突破原有的思维束缚，获得新的思维发展。所以，教师要认真钻研教材，了解学生的学习基础，分析学生的学习情况，正确估计学生有困难的地方，以便在关键时刻给学生指明方法，让学生在解决问题的过程中，迸发出创新思维的火花，逐步树立创新意识。

三、不断渗透入其心

数学思想方法是数学知识发生过程中的概括和提炼升华，是数学的灵魂。在数学教学过程中有意识地渗透一些基本的数学思想方法，有利于培养学生的能力，发展学生的思维。目前，仍有部分老师让学生机械模仿，把强化训练当作课堂的主要内容，就题论题，忽视知识的形成过程，无视学生的认知水平，削弱数学思想方法的提炼，学生苦不堪言，收效甚微。想改变这一模式，需要教师更新教学观念，不断提高专业理论水平，充分挖掘教材和习题中蕴含的数学思想方法，有目的、有计划地渗透到课堂中。

例如，在讲《二元一次方程组的解法》时，教师应让学生明白，代入消元法、加减消元法只是一种手段，目的就是变二元为一元，渗透化归思想。学习《一元二次方程的解法》时再次运用化归思想，变二次方程为一次方程，而直接开方、因式分解等只是解决问题的方法。又如在学习《一次函数的图像和性质》时不断渗透数形结合的思想，为反比例和二次函数的性质研究埋下伏笔。

数学思想方法很难通过言语直接传递给学生，而是需要教师不断渗透，让学生在解决问题的过程中慢慢体会和领悟。

例如：如图6，点A、B分别在 轴和y轴的正半轴上运动，在运动过程中保持AB=4不变，点Q为AB的中点，已知点P的坐标为（4，3），联结PQ，则PQ长的最小值是？

这一道题学生如果仔细研究动点Q的轨迹，不难发现在以O为圆心，2为半径的圆上运动，求PQ长度的最小值实际上就是求点P到圆上点的最小值问题，整个解题过程让学生体验到转化思想的奥妙。

总之，只有让学生摆脱题海战术的煎熬，变被动为主动，变机械训练为发展能力，把培养学生的学习习惯和思维品质摆在首位，才是成功的教学。因此，教师应当不断反思，不断改进，找到适合学生发展的方法，促进师生共同进步。

参考文献：

[1]黄金生.讲题的四种境界[J].数学通报，2009，（10）.

[2]刘儒德.探究学习和课堂教学[M].北京：人民教育出版社，2005.

[3]刘利民.课堂教学中培养学生数学创新意识的三条途径[J].中学数学教学参考，2000，（7）.