同轴微波共振探针诊断大气压等离子体射流的仿真

汪金凤，严 威，陆知遥，张 弛，徐金洲

(东华大学 理学院，上海 201620)

同轴微波共振探针诊断大气压等离子体射流的仿真

汪金凤，严 威，陆知遥，张 弛，徐金洲

(东华大学 理学院，上海 201620)

介绍了一种用于诊断大气压等离子体射流的同轴微波共振探针，利用微波传输线理论分析了探针共振谱与等离子体参数之间的关系.通过仿真模拟得知，探针的共振频率不受等离子体参数的影响，其共振频率与在空气中的共振频率一致；共振半高宽与等离子体的电子密度成正比，与电子温度成反比.根据分析与模拟结果，获得了一种诊断大气压等离子体射流的方法，研究同时表明，探针材料的电导率是产生误差的重要原因.

大气压等离子体射流；同轴共振探针(CRP)；模拟

大气压等离子体有诸多优势，在不需要真空系统的条件下可生成高活性的物种，因而在薄膜沉积、废气处理、杀菌消毒、材料表面改性等方面有广泛的应用.大气压非热等离子体射流可克服传统放电结构中等离子体局限于电极之间的不足，将含有反应活性物种的等离子体引到电极外面，对在任意形状材料表面进行刻蚀处理[1]以及用于医学中的血凝固、创伤修复、对付癌细胞和牙齿美白等方面展现了巨大的潜力[2].目前，大气压等离子体射流主要利用发射光谱来诊断[3-4]，而将低气压等离子体的较为成熟的探针诊断技术如朗缪尔探针和微波共振探针[5]用于高气压等离子体具有一定的局限性[6].为此，本文提出一种基于同轴共振腔结构的探针技术,即采用同轴微波共振探针诊断大气压等离子体射流.

1 同轴微波共振探针共振谱特性分析

同轴微波共振探针是由一个一端短路而另一端开路的同轴谐振腔(同轴传输线)构成，微波能量馈入和反射的测量通过小环耦合实现，如图1(a)所示，即在靠近短路端开一个小孔，将微波电缆芯线与同轴腔的芯线连接，电缆外导体与腔体焊接.

在微波频段，同轴传输线可以等效为分布着电容和电感的电路，因此有图1(b)所示的同轴共振探针等效电路图和表1所示的同轴传输线的分布参数[7].

(a) 同轴传输线

(b) 等效电路图

表1 同轴传输线的分布参数Table 1 The coaxial transmission line distributed parameters

注:R为传输线的电阻；L为传输线的电感；G为传输线的电导；C为传输线的电容；a为内导体外半径；b为外导体内半径；σd为同轴腔中介质的电导率；εd为介质的介电常数；ε0为真空介电常数；μ0为真空磁导率；Rc为趋肤电阻.

根据传输线的理论，输入阻抗Zin可以表达为[7]

(1)

其中：Z0为同轴腔的特征阻抗；α为衰减常数；β为相位常数；l为传输线长度.α和β可以通过同轴共振探针的分布参数表示为

(2)

(3)

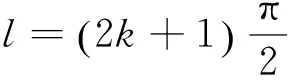
(4)

微波共振谱归一化的半高宽Δf(在共振峰两边功率的值等于最大功率值的1/2处频率之间的宽度)可以表示为[8]

(5)

根据式(2)和(4)，当同轴探针中充满空气时，其中空气的电导率为0，可以得到式(6).

(6)

(7)

其中：等离子体电导率σp和相对介电常数εpr分别为[9]

(8)

(9)

(10)

根据式(10)可知,同轴微波共振探针共振谱的特性由等离子体的参数决定，即半高宽正比于等离子体电子密度，反比于等离子体中电子弹性碰撞频率.

2 仿真结果与讨论

2.1 仿真模型

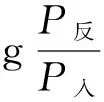
图2 同轴微波共振探针仿真模型Fig.2 The simulation model of coaxial microwave resonant probe

2.2 仿真结果

不同电子温度下探针共振谱随等离子体电子密度的变化如图3所示.从图3可以观察到，探针的共振频率不随等离子体参数的改变而改变，而等离子体密度对共振谱的半高宽的影响非常明显.由于电子的碰撞吸收，随着等离子体电子密度的增加，共振曲线越来越平缓，即共振半高宽随等离子体密度的增加而变宽.如在电子温度为0.8 eV时，当等离子体密度由1.00×1016m-3增加到3.16×1016m-3，

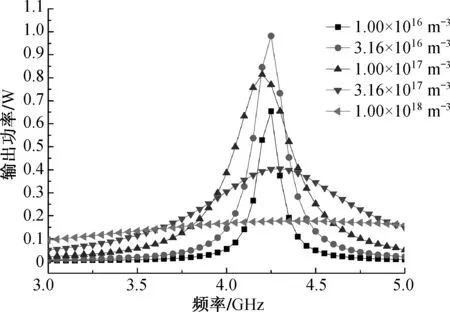
(a) 0.5 eV

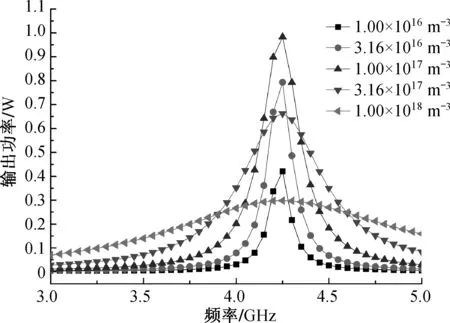
(b) 0.8 eV

(c) 1.1 eV图3 不同电子温度下探针共振谱随电子密度的变化Fig.3 The resonant spectroscopy of coaxial resonator probe versus plasma density at different electron temperature

半高宽由0.140 GHz增加至0.532 GHz. 此外，电子温度对探针共振谱(共振曲线半高宽)也有影响，如等离子体的密度为1.00×1016m-3时,电子温度分别为1.1,0.8,0.5 eV时对应的共振半高宽分别为0.135,0.149,0.161 GHz，即随着电子温度的降低，共振曲线的半高宽变宽.

不同电子温度条件下，归一化半高宽与电子密度的关系如图4所示.从图4可知，共振曲线归一化的半高宽与电子温度成反比，与电子密度成正比.当电子温度为1.1 eV时，随着电子密度的增加，共振曲线归一化半高宽由0.032增加至0.088；当电子温度为0.8 eV时，归一化半高宽随着电子密度的增加由0.032增加至0.129；当电子温度为0.5 eV时，共振曲线归一化半高宽随着电子密度的增加由0.032增加至0.274.上述结果与理论分析结果即式(10)一致.

图4 不同电子温度下归一化半高宽与电子密度的关系Fig.4 The normalized resonance width versus plasma density at different electron temperatures

2.3 大气压等离子体射流诊断方法

由仿真结果可知，共振曲线归一化的半高宽与等离子体电子密度成正比，与电子温度成反比，由式(9)可知，其与电子弹性碰撞频率也成反比.因此，由式(10)可得到同轴微波共振探针测量大气压等离子体射流的电子密度计算式如式(11)所示.

(11)

广泛用于材料处理的AtomfloTM500常压等离子体射流装置在放电区域产生的等离子体电子密度为1017～1018m-3,且其喷射出来的等离子体的电子密度会有所降低，所以本文在仿真过程中设定电子密度值为1016～1018m-3.

当等离子体电子温度为0.5 eV时，由仿真得到的共振频率与共振谱的半高宽代入式(11)计算出的电子密度，以及计算值与设定值之间的相对误差如表2所示.由于当电子密度为1018m-3时，共振峰已不明显，相应的半高宽很宽，此时已经无法计算出电子密度，所以利用本文的探针进行诊断时，等离子体的电子密度需低于1018m-3.从表2可以观察到，探针测量大气压等离子体射流电子密度的相对误差均低于26%.其中探针材料的电导率是造成误差的重要因素，利用仿真模拟的方法，在等离子体电子密度为1.00×1016m-3时，将探针材料的电导率从5.998×107S/m增加到 5.998×1010S/m，则相对误差由25.0%降低到5.4%；当电子密度为1017m-3时，相对误差由8.0%降低到0.5%.因此，选择较好的导体来制作探针是十分必要的.

表2 仿真的计算结果及其与设定值间的误差Table 2 The simulation calculation results and error between the calculation results and the set points

3 结 语

大气压等离子体射流在众多领域都有着非常重要的应用.为了更好地利用这种等离子体源，对其参数的诊断是十分必要的.基于同轴共振腔的结构，本文提出一种同轴微波共振探针结构，并利用传输线理论对其共振频率和微波功率共振谱的特征进行分析，建立探针模型并采用COMSOL 4.2a对其进行仿真研究，验证了大气压等离子体射流参数(电子密度与电子温度)与探针共振频率和共振谱特征参数(半高宽)的关系，即共振曲线归一化的半高宽随电子密度的增加线性增加，而与电子温度(碰撞频率)成反比.由此提出了一种同轴微波共振诊断大气压等离子体射流参数的方法.

[1] JEONG J Y,BABAYAN S E,TU V J,et al.Etching materials with an atmospheric-pressure plasma jet [J]. Plasma Sources Science and Technology,1998,7(3): 282-285.

[2] PARK G Y,PARK S J,CHOI M Y,et al.Atmospheric-pressure plasma sources for biomedical applications [J]. Plasma Sources Science and Technology,2012,21(4): 43001-43021.

[3] SCHULZ-VON DER GATHEN V,SCHAPER L,KNAKE N,et al.Spatially resolved diagnostics on a microscale atmospheric pressure plasma jet [J]. Journal of Physics D: Applied Physics,2008,41(19): 94004-94011.

[4] XIONG Q,NIKIFOROV A Y,GONZALEZ M,et al. Characterization of an atmospheric helium plasma jet by relative and absolute optical emission spectroscopy [J]. Plasma Sources Science and Technology,2013,22(1): 15011-15023.

[5] PIEJAK R B,GODYAK V A,GARNER R,et al. The Hairpin resonator: A plasma density measuring technique revisited [J]. Journal of Applied Physics,2004,95(7): 3785-3791.

[6] SANDS B L,SIEFERT N S,GANGULY B N. Design and measurement considerations of hairpin resonator probes for determining electron number density in collisional plasmas [J]. Plasma Sources Science and Technology,2007,16(4): 716-727.

[7] 王一平，郭宏福.电磁波：传输·辐射·传播[M].西安：西安电子科技大学出版社，2007:26-30.

[8] XU J,NAKAMURA K,ZHANG Q,et al. Simulation of resistive microwave resonator probe for high-pressure plasma diagnostics [J]. Plasma Sources Science and Technology,2009,18(4): 45009-45018.

[9] 迈克尔·A·力伯曼，阿伦·J·里登伯格.等离子体放电原理与材料处理[M].蒲以康，等，译. 北京：科学出版社，2007：72-73.

Simulation of Coaxial Microwave Resonator Probe for Diagnosing Atmospheric Pressure Plasma Jet

WANGJin-feng,YANWei,LUZhi-yao,ZHANGChi,XUJin-zhou

(College of Science,Donghua University,Shanghai 201620,China)

The coaxial microwave resonator probe used in the diagnosis of atmospheric pressure plasma is introduced,the relation between the resonant spectroscopy of coaxial resonator probe (CRP) and atmospheric pressure jet plasma parameters is analyzed by using the theory of microwave transmission line. The simulation result shows that the resonant frequency does not change with the plasma parameters,and it is consistent with the resonant frequency in the air. The resonant full width of half maximum is proportional to plasma electron density and inversely proportional to electron temperature. According to the results of analysis and simulation,the method of diagnosing atmospheric pressure plasma jet with CRP is obtained. The electrical conductivity of probe material is the important cause of the error.

atmospheric pressure plasma jet; coaxial resonator probe (CRP); simulation

1671-0444(2015)01-0125-05

2013-10-21

国家自然科学基金资助项目(11075033)

汪金凤(1988—)，女，辽宁锦州人，硕士，研究方向为等离子体物理.E-mail: jfengw@163.com

徐金洲(联系人)，男，教授,E-mail: jzxu@dhu.edu.cn

O 536

A