基于阿苏尔杆组的混合驱动机构动力学建模分析

孙志宏， 翟祥勇， 李子军

(1. 东华大学 机械工程学院，上海 201620； 2. 山东日发纺织机械有限公司，山东 聊城 252000)

基于阿苏尔杆组的混合驱动机构动力学建模分析

孙志宏1， 翟祥勇1， 李子军2

(1. 东华大学 机械工程学院，上海 201620； 2. 山东日发纺织机械有限公司，山东 聊城 252000)

通过对定轴转动的刚体构件、II级杆组和RR-RR-RR型III级杆组进行动力学分析，建立了一种新的机构动力学分析计算模型，根据模型对混合驱动机构进行拆分，并对得到的相应杆组模块进行计算. 最后，运用该计算模型对一种混合驱动九杆机构进行实例分析，得到常速电机和伺服电机的平衡力矩，证实此建模计算分析方法可用于简化混合驱动机构动力学参数的计算.

混合驱动；阿苏尔杆组；机构分析；动力学分析

混合驱动机构通常指由常速电机和伺服电机驱动的具有2自由度的机构[1-2].文献[3]对由常速电机和伺服电机组成的混合驱动机构进行动力学仿真试验可知，常速电机承担了系统的大部分功率，伺服电机为运动调节驱动件.文献[4]建立了一个2自由度的混合驱动七杆机构动力学模型，并将自动控制引入到该机构中.文献[5]在对一种混合驱动七杆机构运动分析的基础上，基于拉格朗日方程的方法，建立了混合驱动机构系统的刚性全局动力学方程模型.文献[6]以一种几何位置关系为基础，介绍了可控连杆机构动力学分析的简明通用方法.文献[7]从连杆机构学与机器人的理论比较中得到混合驱动机械系统建模的理论依据，并介绍了混合驱动机械系统成组运动规律.文献[8-9]对混合驱动五杆机构系统全局动力学模型建模进行研究.文献[10]提出了一种模块化机器人系统运动学和动力学建模方法.上述研究都没有考虑基于阿苏尔杆组的动力学建模方法.为此，本文提出一种基于阿苏尔杆组的混合驱动机构动力学问题的建模分析方法.

1 定轴转动的刚体构件动力学分析

图1所示为定轴转动的刚体，其质心为s1，合外力为(F1x,F1y)，合外力矩为T1，铰链点P1和P2对杆1作用的力分别为(FP1x,FP1y)和(FP2x,FP2y)，驱动力矩为Md，质心加速度为(as1x,as1y)，转动惯量为Js1，角加速度为β1，根据力的平衡条件有

图1 刚体机构动力学分析Fig.1 Dynamic analysis of rigid body

(1)

即

(2)

其中：xP1P2=xP2-xP1； yP1P2=yP2-yP1； xs1P1=xP1-xs1；ys1P1=yP1-ys1.

(3)

若式(2)中任意时刻的as1x,as1y,β1,m1,Js1,T1,F1x,F1y,FP2x,FP2y为已知量,根据式(3)即可计算得到电机的驱动力矩Md及固定铰链点P1处的约束力FP1x和FP1y.

2 II级阿苏尔杆组动力学分析

II级阿苏尔杆组有RRR,RRP,RPR,PRP,PPR这5种类型，如图2所示.

图2 II级阿苏尔杆组类型Fig.2 II Assur group types

2.1 RRR型II级杆组动力学分析

图3(a)所示为RRR型II级杆组动力学分析示意图,设各杆质心分别为s1和s2，在质心s1和s2处分别受到的合外力为(F1x,F1y)和(F2x,F2y)，合外力矩为T1和T2，且转动惯量分别为Js1和Js2.外副铰链点P1和P2处受到外界作用力分别为(FP1x,FP1y)和(FP2x,FP2y);内副铰链点P3处无外界作用力约束.将其拆开进行力平衡分析，如图3(b)和3(c)所示.

图3 RRR型II级杆组动力学分析Fig.3 Dynamic analysis of RRR II Assur group

根据力的平衡条件，由图3(b)可得

(4)

即

(5)

其中：xP1P3=xP3-xP1； yP1P3=yP3-yP1； xs1P3=xP3-xs1； ys1P3=yP3-ys1.

根据力的平衡条件，由图3(c)可得：

(6)

即

(7)

其中：xP2P3=xP3-xP2； yP2P3=yP3-yP2； xs2P3=xP3-xs2； ys2P3=yP3-ys2.

将式(5)和(7)联立并消去(FP3x,FP3y)得

(8)

写成矩阵形式：NX=B-B0

(9)

其中：

B=[m1as1x+m2as2xm1as1y+m2as2y

Js1β1Js2β2]T,

且b1=F1x+F2x,b2=F1y+F2y,b3=T1+ys1P3F1x-xs1P3F1y,b4=T2+ys2P3F1x-xs2P3F1y;

xpipj=xpj-xpi,ypipj=ypj-ypi,

(i=1,2; j=1,2).

对任意时间t，矩阵N=N(t)是可逆的，将矩阵N,B,B0作为已知条件可得

X=N-1(B-B0)

(10)

显然，如果该RRR型杆组在P3点处有外力作用，仍可用上述方法进行分析.

2.2 RRP,RPR,PRP,PPR型II级杆组动力学分析

RRP,RPR,PRP,PPR型II级杆组都含有移动副.如图4所示为RRP型II级杆组，在移动副P2处受到外力的作用，对其进行力的平衡分析可得式(8)，与RRR型II级杆组相同.同理对其他类型含有移动副的II级杆组进行动力学分析，得到的计算方程式与RRR型II 级杆组计算方程式相同.

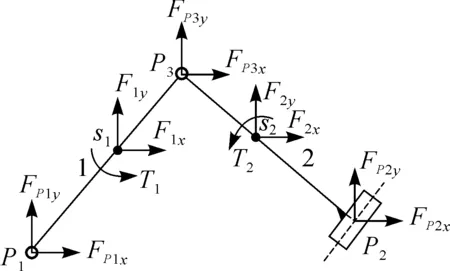
图4 RRP型II级杆组动力学分析Fig.4 Dynamic analysis of RRP II Assur group

3 III级杆组动力学分析

III级杆组的类型有很多种，但常用类型是RR-RR-RR型III级杆组，本文主要对RR-RR-RR型III级杆组进行动力学建模分析，其过程如下所述.

如图5(a) 所示为RR-RR-RR型III级杆组动力学分析示意图,设其各杆质心分别为s1,s2,s3,s4，在质心处受到的合外力分别为(F1x,F1y)，(F2x,F2y)，(F3x,F3y)，(F4x,F4y)，合外力矩分别为T1,T2,T3,T4，各杆质量分别为m1,m2,m3,m4，转动惯量分别为Js1,Js2,Js3,Js4，外副铰链点P1,P2,P3处受到的合外力为(FP1x,FP1y)，(FP2x,FP2y)，(FP3x,FP3y)，内副铰链点Q1,Q2,Q3处无外界作用力约束.对该III级杆组拆开进行力平衡分析，如图5(b)～5(e)所示.

根据力的平衡条件，由图5(b)可得

(11)

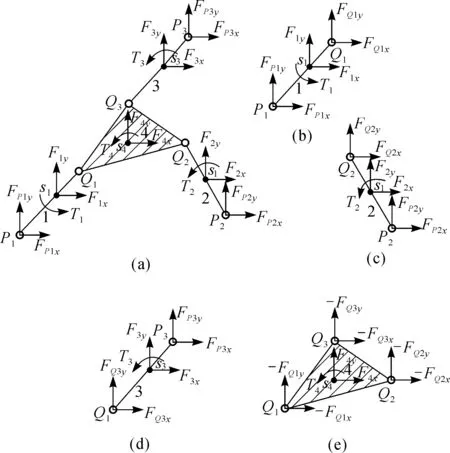
图5 RR-RR-RR型III级杆组动力学分析Fig.5 Dynamic analysis of RR-RR-RR III Assur group

即

(12)

其中:xP1Q1=xQ1-xP1； yP1Q1=yQ1-yP1； xs1Q1=xQ1-xs1； ys1Q1=yQ1-ys1.

同理，根据力的平衡条件，由图5(c)～5(e)分别得式(13)～(15).

(13)

其中：xP2Q2=xQ2-xP2； yP2Q2=yQ2-yP2； xs2Q2=xQ2-xs2； ys2Q2=yQ2-ys2.

(14)

其中：xP3Q3=xQ3-xP3； yP3Q3=yQ3-yP3； xs3Q3=xQ3-xs3；ys3Q3=yQ3-ys3.

(15)

其中：xQis4=xs4-xQi；yQis4=ys4-yQi,i=1,2,3.

将式(12)～(15)联立，得

NX=B-B0

(16)

其中：

B=

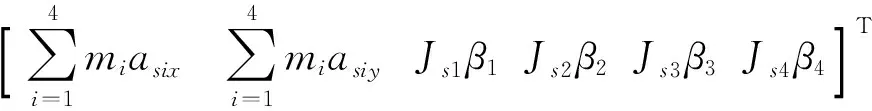
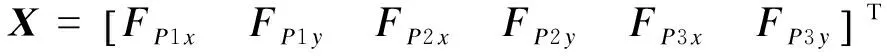
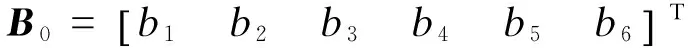
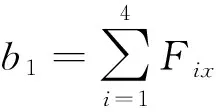
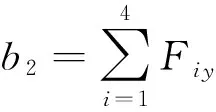
b3=T1+ys1Q1F1x-xs1Q1F1y,

b4=T2+ys2Q2F2x-xs2Q2F2y,

b5=T3+ys3Q3F3x-xs3Q3F3y,

xPiQi=xQi-xPi,yPiQi=yQi-yPi,

xQis4=xs4-xQi,yQis4=ys4-yQi,

i=1,2,3.

对任意时间t，矩阵N=N(t)是可逆的，将式(16)中矩阵N,B,B0作为已知条件代入可求出：

X=N-1(B-B0)

(17)

显然，如果该RR-RR-RR型III级杆组在Q1,Q2,Q3这3点处有外力作用时，仍可用上述方法进行分析.

4 实例分析

图6 混合驱动九杆机构Fig.6 Hybrid machine nine-bar mechanism

将图6(a)所示的混合驱动九杆机构进行拆分，得到2个定轴转动的刚体构件和3个RRR型II级杆组，如图6(b)所示. 采用基于阿苏尔杆组的建模方法，由已知条件可知，铰链点P7处无外界约束力作用，对杆6和杆7组成的RRR型杆组进行分析，可求得P6和P8点处外界作用约束力FP6和FP8.利用FP8对杆8进行分析，可得伺服电机平衡力矩.利用FP6对杆4和5组成的RRR型杆组进行分析，可求得P4和P5点处外界作用的约束力FP4和FP5.利用FP4对杆2和3组成的RRR型杆组进行分析，可求得P2和P3点处外界作用的约束力FP2和FP3.利用FP2对杆1进行分析，可求得常速电机的平衡力矩.通过Matlab编程分析得到常速电机和伺服电机的平衡力矩分别如图7和8所示.显然，本文这种将混合驱动九杆机构拆分成阿苏尔杆组依次进行动力学分析的方法是可行的，其取代了基于单构件进行动力学分析[11]的方法，简化了混合驱动机构动力学参数的计算过程.

图7 常速电机平衡力矩图

图8 伺服电机平衡力矩图

5 结 语

本文通过对定轴转动刚体构件、II级杆组和RR- RR-RR型III级杆组进行动力学分析，提出了对其进行阿苏尔杆组动力学模型建立的方法，并通过实例计算分析，验证了该方法的有效性.这种计算分析方法简化了混合驱动机构动力学参数的计算过程.但是本文的建模方法是在刚性机构的基础上建立的，同时也没有考虑常速电机的速度波动等因素的影响，因此该建模方法有待再深入研究分析.

[1] TOKUZ L C. Hybrid machine modeling and control[D]. Liverpool: Liverpool Polytechnic University,1992.

[2] 张珂,王生泽,王永兴.基于重复控制的平面可控机构控制系统研究[J]. 东华大学学报:自然科学版,2006,32(3): 52-55.

[3] GREENOUGH J D,BRADSHAW W K,GILMARTIN M J. Design of hybrid machines[C]//Proceedings of the 9th IFTMM World Congress. Milan,Italy,1995: 2501-2505.

[4] KIRECCI A,DLULGER L C. A study on a hybrid actuator[J]. Mechanism and Machine Theory,2000,35 (8): 1141-1149.

[5] DLULGER L C,KIRECCI A,TOPALBEKIROGLU M. Modeling and simulation of a hybrid actuator[J]. Mechanism and Machine Theory,2003,38 (5): 395-407.

[6] 王生泽,刘素平.可控连杆机构动力学分析的一般方法研究[J]. 机械设计与研究,2002(S): 89-90.

[7] 张新华,张策.混合驱动机械系统建模的理论依据[J].机械科学与技术,2001,20(6): 857-859.

[8] 张珂. 混合驱动连杆机构系统动力学建模、优化与控制研究[D]. 上海：东华大学机械工程学院，2005: 12-13.

[9] OUYANG P R,LI Q,ZHANG W J,et al,Design,modeling and control of a hybrid machine system[J]. Mechatronics,2004,14(10): 1197-1217.

[10] BI Z M,GRUVER W,ZHANG W J,et al. Automated modeling of modular robotic configurations[J].Robotics and Autonomous Systems,2006,54(12): 1015-1025.

[11] 张策.机械动力学[M].2版.北京:高等教育出版社,2008:24-30.

Dynamic Modeling Analysis by Assur Groups on Hybrid Actuation Mechanisms

SUNZhi-hong1,ZHAIXiang-yong1，LIZi-jun2

(1.CollegeofMechanicalEngineering,DonghuaUniversity,Shanghai201620，China;2.ShandongRifaTextileMachineryLimitedCompany,Liaocheng252000,China)

Based on the dynamics analysis of the fixed axis rotation of rigid body components,II groups and RR-RR-RR III group,a new mechanism dynamic analysis and calculation model was built. Then the model was used to calculate the group models which divided by the hybrid actuation mechanism. At last,the count-balance moment of the constant speed motor and the servo motor were got by the analysis of hybrid actuation nine-bar mechanism,which confirmed that the mentioned method could be used to simplify the kinetic parameters calculation of the hybrid actuation mechanism.

hybrid actuation; Assur groups; mechanism analysis; dynamic analysis

1671-0444(2015)01-0091-05

2013-09-24

孙志宏(1968—)，女，上海人，教授，博士，研究方向为机械设计及理论、立体织造技术与装备.E-mail: zhsun@dhu.edu.cn

TH 122

A