伪Fibonacci数列及其推广
邓勇
(喀什师范学院 数学系,新疆 喀什市 844006)
伪Fibonacci数列及其推广
邓勇
(喀什师范学院 数学系,新疆 喀什市 844006)
探讨了由非齐次线性递推关系gn+2=gn+1+gn+Atn,n≥0,A≠0且t≠0所定义的数列{gn}的一些基本性质;利用Elmore技巧和{gn}的指数生成函数推广了{gn},得到一个新的序列G(nx),并证明了Gn(x)满足线性递推关系Gn+2=Gn+1+Gn+Atnext;最后,利用广义三角函数和新定义的序列{Q(nx)}再次扩展了序列{G(nx)},给出并证明了它所满足的递推关系.
递推关系;广义三角函数;伪Fibonacci数列
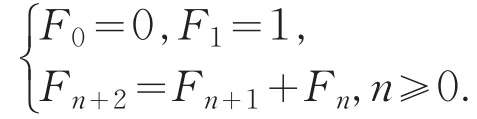
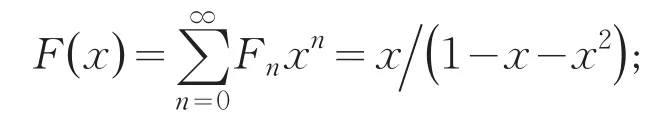

本文将探讨由更一般的二阶非齐次线性递推关系所定义的数列——伪Fibonacci数列{gn}以及由其指数生成函数所定义的新序列{Gn(x)};随后,对三角函数进行了推广,并利用广义三角函数和Pethe-Phadte技巧再次将{gn}推广到了新的序列{Qn(x)}.
1 伪Fibonacci数列{gn}的定义
设α,β是Fibonacci数列{Fn}的特征方程x2-x-1=0的两个互异根.所谓伪Fibonacci数列{gn}是指由二阶非齐次线性递推关系

所确定的数列.显然,当A=0时,{gn}则退化为{Fn}.
不难推出{gn}的通项公式、生成函数和指数生成函数分别为
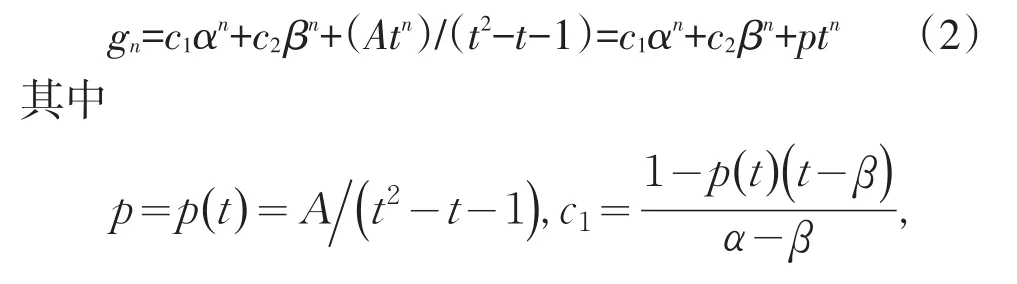
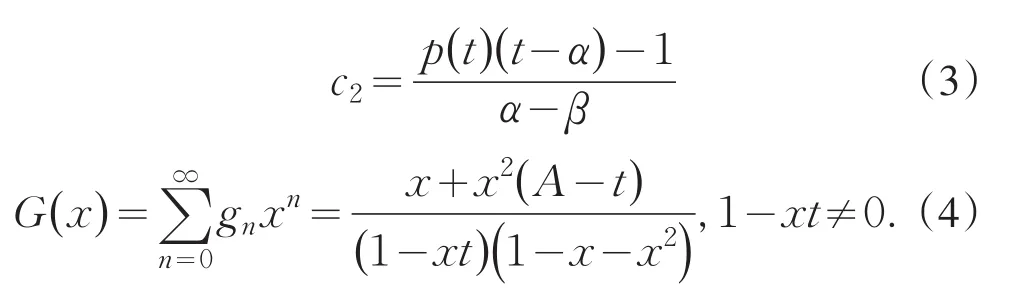
特别地,当A=0时,G(x)=x/(1-x-x2)恰好是{Fn}的生成函数.
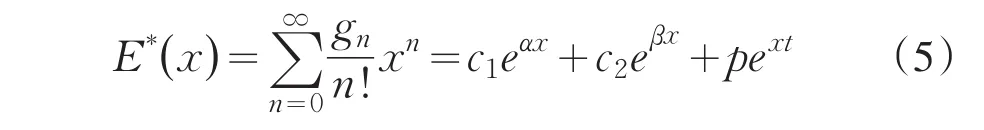
其中c1和c2如(3)所定义且当A=0时,p=0,.此时,恰为{Fn}的指数生成函数[5].
2 应用Elmore方法推广{gn}
根据Elmore方法,利用伪Fibonacci数列{gn}来定义一个新序列.为此,设
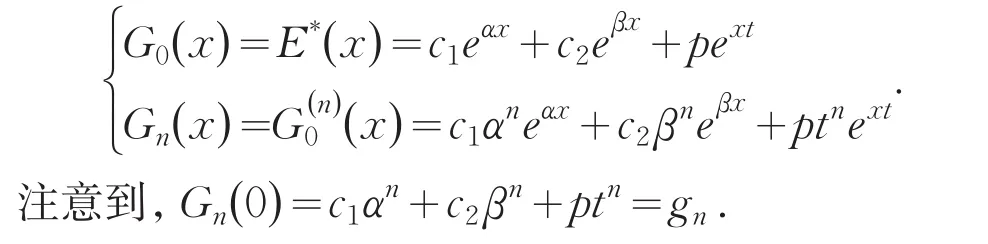
定理1序列{Gn(x)}满足非齐次线性递推关系

特别地,当A=0时,{Gn(x)}就退化为{Fn}.
证明 递推关系(6)的右边等于
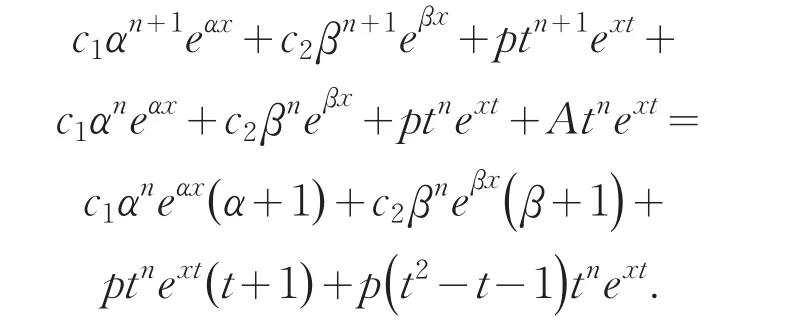
因α和β是x2-x-1的根,即α+1=α2且β+1=β2,故上式可进一步化简为

3 应用广义三角函数推广{gn}
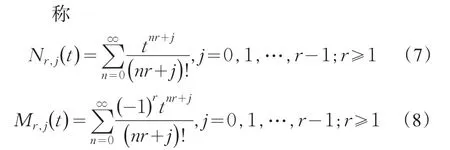
为广义三角函数[6].由函数的幂级数表示,容易看出

若对(7)逐项微分,则有

下面,利用广义三角函数首先推广伪Fibonacci数列{gn},然后再应用Pethe-Phadte[7-8]技巧定义一个新序列{Qn(x)}.为此,设

其中α*=α1/r,β*=β1/r,t*=t1/r,r∈Z+.陆续定义序列{Qn(x)}的其他各项分别如下:
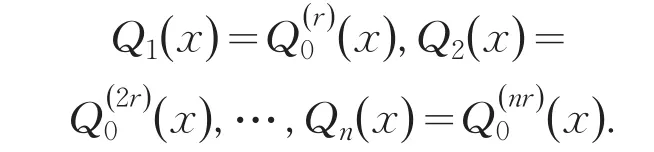
即Q1(x)是Q0(x)关于x的r阶导数,Q2(x)是Q0(x)关于x的2r阶导数,…,Qn(x)是Q0(x)关于x的nr阶导数.由Q0(x)的定义,并利用可得

显然,当r=1,x=0,A=0时,{Qn(x)}就退化为{Fn}.
定理2序列{Qn(x)}满足非齐次线性递推关系

证明 递推关系(9)的右边等于
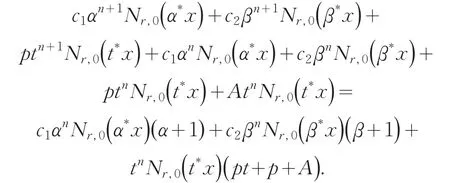
因α和β是x2-x-1的根,故将

代入上式并经化简后,(9)的右边最终可化为

[1]劳会学.Fibonacci数列通项公式的四个直接证明[J].数学的实践与认识,2007,37(15):180-182.
[2]张新娟.斐波那契数列通项公式的求法[J].高等数学研究,2009,12(4):56-59.
[3]吴振奎.斐波那契数列欣赏[M].黑龙江:哈尔滨工业大学出版社,2012.
[4]Elmore M.Fibonacci Functions[J].Fibonacci Quarterly,1967,5(4):371-382.
[5]周炜.组合数学[M].北京:清华大学出版社,2011.
[6]耿济.自然指数函数展开式的多重分割法(四)——抽象三角函数[J].海南大学学报:自然科学版,1997,15(1):1-8.
[7]梁艳楠.Fibonacci数列的推广与应用[D].大连理工大学,2008.
[8]Pethe S P,Phadte C N.A generalization of the Fibonacci se⁃quence[J].Applications of Fibonacci numbers,1992(5):465-472.
责任编辑:毕和平
Pseudo Fibonacci Sequence and Its Generalization
DENG Yong
(Department of Mathematics,Kashgar Teacher’s College,Kashgar844006,China)
First,the basic properties of the sequence{gn}that was defined by a non-homogeneous linear recurrence rela⁃tiongn+2=gn+1+gn+Atn,n≥0,A≠0t≠0 were discussed;Secondly,the sequence{gn}was generalized by using the techniques of Elmore and exponential generating function of{gn}.Thus,we got a new sequence that satisfied a linear recurrence relationGn+2=Gn+1+Gn+Atnext;finally,the sequence{Gn(x)}was generalized again by using generalized trigonometric functions and rede⁃fined sequence{Gn(x)},in addition,its recurrence relation was given and proved.
recurrence relation;generalized circular function;pseudo Fibonacci sequence
O 171
A
1674-4942(2015)02-0139-03
2015-01-07

