考虑误差的行星滚柱丝杠副滚柱承载分布

马尚君，刘 更，付晓军，张文杰，乔 冠

(陕西省机电传动与控制工程实验室(西北工业大学)，710072西安)

行星滚柱丝杠副(planetary roller screw mechanism，PRSM)是一种可将旋转运动转换成直线运动的机械传动装置［1］，广泛应用于直线机电作动系统［2-3］、医疗设备［4］和精密机床［5］等需要直线作动的场合.建立考虑误差的滚柱螺纹牙承载分布计算模型对于PRSM参数设计和研究其传动性能具有重要意义，但目前关于PRSM的研究主要集中于运动学［6］、接触特性［7］及传动效率［8］和传动精度［9］等方面，关于滚柱承载分布的研究还不深入.杨家军等［10］基于赫兹接触变形与轴向变形的关系，建立了承载分布计算公式，并进一步研究了PRSM刚度特性.Jones等［11］采用直接刚度法，计算了丝杠侧和螺母侧螺纹承载分布，研究了滚柱和螺纹牙数目对PRSM刚度的影响规律.Rys等［12］将滚动体等效成矩形单元，建立了剪切力作用下丝杠侧和螺母侧承载分布计算公式，并与有限元解进行了对比验证.上述研究为PRSM承载分布和传动性能研究奠定了理论基础，但均未计入误差影响，而且螺纹结构参数等因素对滚柱承载分布的影响规律研究尚不充分.

本文基于文献［10］承载分布求解思路，即在丝杠受轴向拉力和螺母受轴向压力作用下，其相对应的丝杠伸长量和螺母的压缩量与在第i个和第i+1个螺纹牙处的赫兹变形的轴向分量之差相等，考虑误差影响构建PRSM滚柱承载分布计算模型，并进一步研究负载、接触角、螺旋升角、滚柱螺纹牙数和螺纹副材料弹性模量比等因素对滚柱承载分布的影响规律.

1 PRSM滚柱承载分布建模

1.1 模型假设

根据PRSM结构特点和传动原理，作如下假设:1)多个滚柱承载分布相同;2)丝杠侧与螺母侧承载分布一致，且丝杠侧和螺母侧误差分布相同;3)丝杠和螺母材料属性一致，滚柱材料属性不同于丝杠和螺母;4)在轴向载荷作用下，几何误差不会导致丝杠、螺母和滚柱接触角发生变化.

1.2 考虑误差的PRSM滚柱承载分布建模

在PRSM传动中，滚柱螺纹牙型通常加工成球面，多个滚柱同时参与啮合，以提高承载能力和传动平稳性.滚柱螺纹牙具有多体多点接触特征.基于模型假设，滚柱与丝杠和螺母的接触状态如图1.

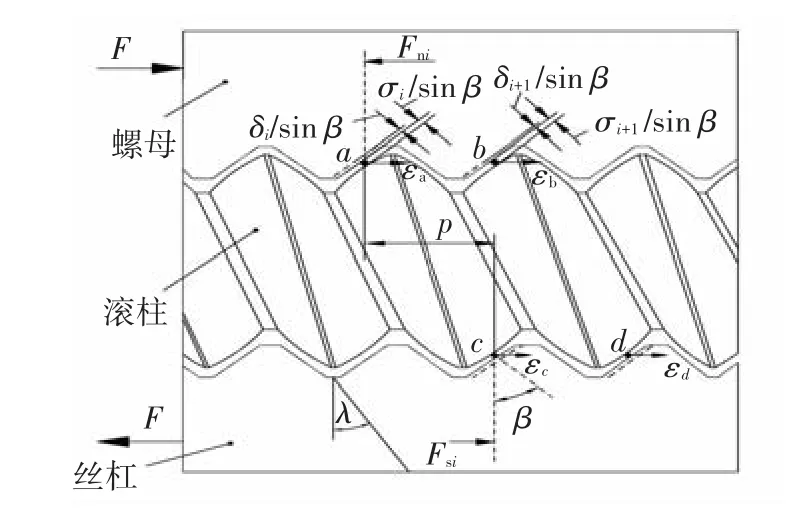
图1 考虑误差的滚柱承载分布模型

图1为滚柱第i个螺纹牙在丝杠轴向力Fsi和螺母轴向力Fni作用下的平衡状态，实线和虚线分别表示滚柱螺纹牙与丝杠和螺母螺纹牙接触发生弹性变形前后的状态.a点和b点为第i个螺纹牙和第i+1个螺纹牙与螺母的接触点，c点和d点为第i个螺纹牙和第i+1个螺纹牙与丝杠的接触点.σi+1和σi分别表示第i+1个螺纹牙与第i个螺纹牙总的几何误差.εa、εb、εc和εd分别表示 4个接触点的轴向偏差.δi+1和δi分别表示第i+1个螺纹牙与第i个螺纹牙弹性变形量.由图1可知，滚柱相邻螺纹牙上接触点a和b的几何误差在轴截面的法向分量分别为σi+1/sinβ和σi/sinβ，同理，滚柱相邻螺纹牙上接触点a和b的弹性变形量在轴截面的法向分量分别为δi+1/sinβ和δi/sinβ.根据力平衡关系可知［13］

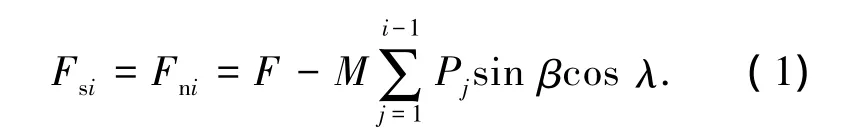
其中:Fsi和Fni分别为滚柱第i个螺纹牙在丝杠侧和螺母侧所受轴向力，Pj为第j个螺纹牙所受法向力，β为接触角，λ为螺旋升角.F为总轴向力.总轴向力与滚柱螺纹牙载荷的关系可以表示为

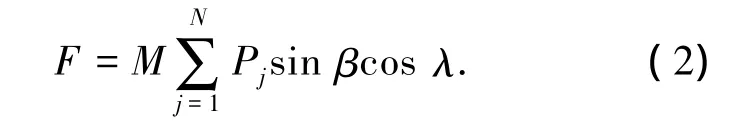
其中:M为滚柱数量，N为单个滚柱上螺纹牙数目.

由图1几何关系可知，第i个螺纹牙和第i+1个螺纹牙的几何误差在轴向的分量分别为σi/sinβcosλ和σi+1/sinβcosλ，则第i个螺纹牙和第i+1个螺纹牙产生的弹性变形量在轴向的分量分别为δi/sinβcosλ和δi+1/sinβcosλ.

由于在第i到i+1个螺纹牙之间，PRSM受到丝杠及螺母对滚柱的轴向拉力及压力作用，故在i与i+1螺纹牙处的丝杠侧和螺母侧的轴向偏差分别为

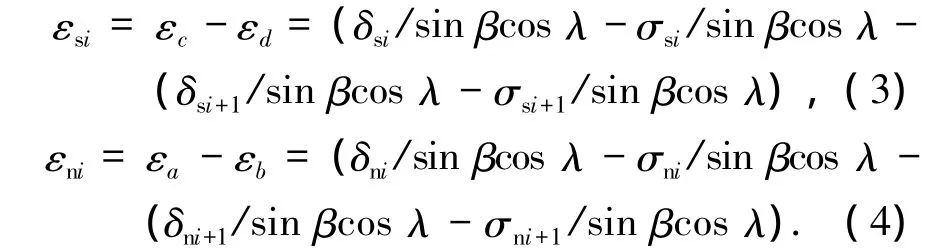
式(3)和式(4)等号右边第一项表示第i个螺纹牙的两个接触点含误差的相对轴向偏差，第二项表示第i+1个螺纹牙的两个接触点含误差的相对轴向偏差.根据赫兹接触理论可知［14］

式(5)、(6)中，fs、fn分别表示两接触侧刚度系数.

根据PRSM受力状态，将丝杠和螺母分别等效为圆柱和空心圆柱，则丝杠受到的轴向拉伸量和螺母受到的轴向压缩量分别为

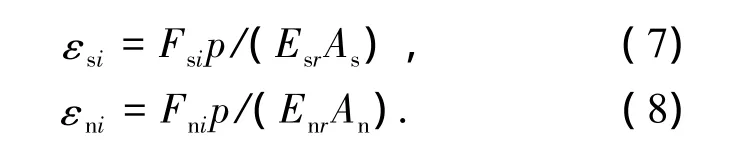
其中:Esr、Enr分别为两接触物体材料的当量弹性模量，As和An分别为丝杠和螺母的有效接触面积，p为螺距.

根据赫兹接触变形与轴向变形关系，在丝杠受轴向拉力和螺母受轴向压力作用下，相对应的丝杠伸长量及螺母的压缩量与在第i到i+1个螺纹牙的赫兹接触变形量的轴向分量之差相同.

将式(1)、(2)、(5)～(8)代入式(3)、(4)，再将式(3)和式(4)相加，可得考虑误差的滚柱螺纹牙承载分布计算模型:

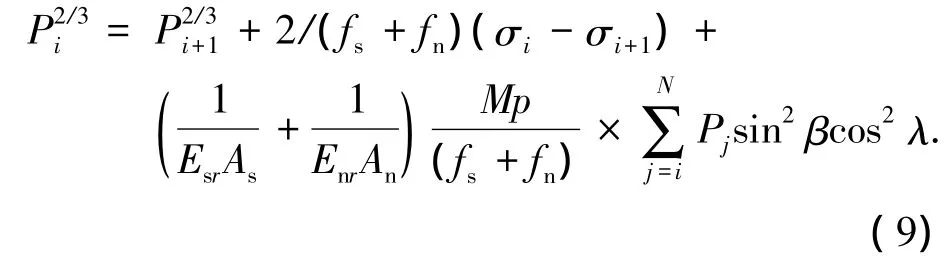
由式(9)可见，误差项(等式右边第二项)直接影响接触点接触状态，导致滚柱螺纹牙各接触点承载分布发生变化.

1.3 模型验证

为了验证本文模型的正确性，并与文献［11］采用直接刚度法的计算结果进行对比，故采用文献［11］初始参数(如表1所示).直接刚度法是将PRSM等效成一个弹簧系统，根据接触点变形、刚度和力的关系建立矩阵方程，求解各接触点力.本文是根据PRSM两接触侧相邻螺纹牙变形协调关系导出了含误差的承载分布计算模型.文献［11］求解承载分布没有考虑误差影响，故式(9)中等号右边第二项为零，计算结果如图2所示.

表 1 PRSM 参数［11］

由图2可见，本文滚柱承载分布计算结果与文献［11］计算结果吻合很好，特别是滚柱各螺纹牙承载比例范围和前几个螺纹牙承载变化趋势吻合程度较高，故验证了本文所建模型的正确性.

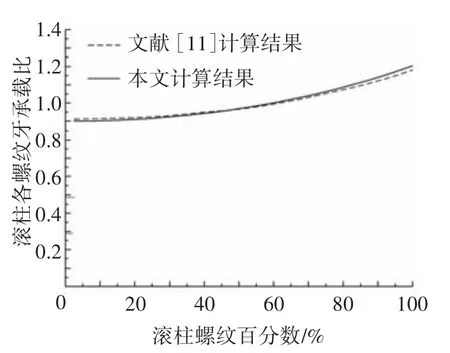
图2 滚柱各螺纹牙承载比例对比

2 PRSM滚柱承载分布规律

2.1 随机误差分布

为了便于研究，将各个螺纹牙载荷Fi对总载荷F进行量纲一化，并假设PRSM的几何误差是一种随机误差，且服从正态分布，图3给出了平均误差为 0，标准方差Sd=0.002 7 μm 的误差曲线图.

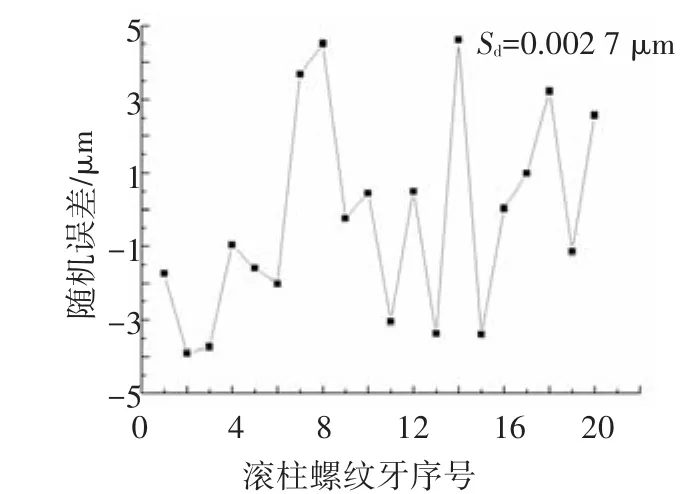
图3 滚柱螺纹牙随机误差分布

2.2 不同轴向力对承载分布的影响

滚柱螺纹牙承载分布与负载大小直接相关，选取负载为 5、10、20、50、80 kN，接触角和螺旋升角分别为45°和11.532 6°，采用图3所示误差分布.Es/Er=1∶1，表示丝杠和滚柱材料弹性模量相同.计算结果如图4所示.

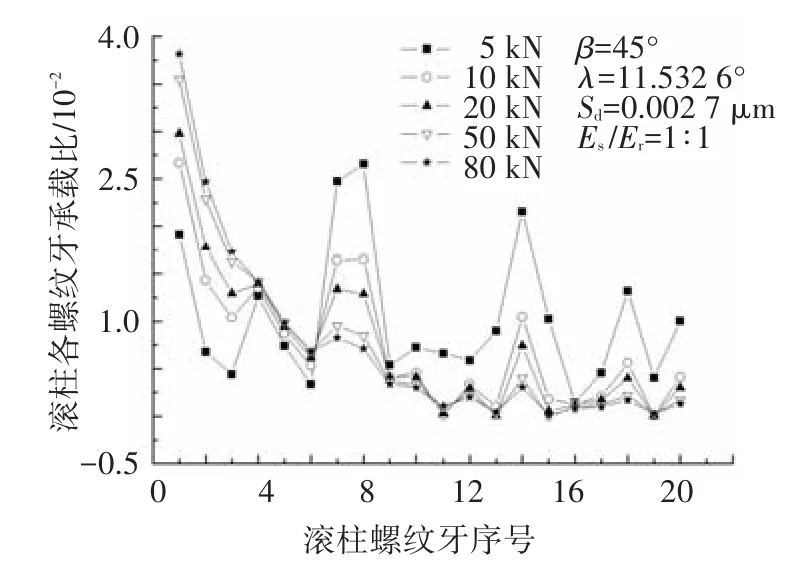
图4 载荷对滚柱螺纹牙承载分布的影响

由图4可见，在相同误差分布下，负载越小，滚柱承载分布波动越大，而且前3个螺纹牙承载比例相差较大.当负载达到50 kN以上时，滚柱螺纹牙的承载分布基本保持不变，且波动减小.随着负载增大，各个螺纹牙的承载比例变化减小，这恰好反映了PRSM在承受较大轴向载荷时，能够保持较高的传动精度和平稳性的特点.结合图3可知，正误差螺纹牙承载较大，说明负误差能够改善螺纹牙承载分布，而且负误差更有利于降低前3个螺纹牙承载比例，从而避免过载导致牙断裂和出现脱啮现象.

2.3 接触角对承载分布的影响

选取接触角分别为 25°、30°、35°、40°、45°和50°，负载为50 kN，螺旋升角、误差分布和材料弹性模量比不变.接触角对滚柱螺纹牙承载分布的影响规律如图5所示.

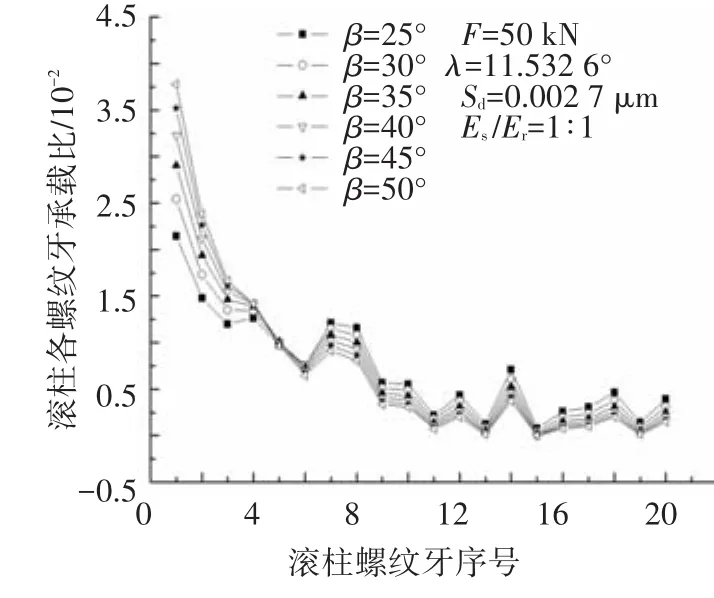
图5 接触角对滚柱螺纹牙承载分布的影响

由图5可见，取不同接触角值，滚柱螺纹牙承载分布变化趋势保持不变.接触角越大，前3个螺纹牙承载比例变化越大，均呈增大趋势，这主要是因为接触角增大，刚度系数fs和fn均减小.在相同误差分布和负载下，接触角越小，滚柱螺纹牙承载分布相对更均匀，而且在给定接触角下，负误差更有利于降低前3个螺纹牙承载比例.

2.4 螺旋升角对承载分布的影响

选取螺旋升角分别为 2.336 9°、4.666 0°、6.979 8°、9.271 0°和 11.532 6°，对应螺距分别为p=1、2、3、4、5，负载为 50 kN，接触角、误差分布和材料弹性模量比不变.接触角对滚柱螺纹牙承载分布的影响规律如图6所示.

对比图6和图5可知，误差分布和螺旋升角对滚柱螺纹牙承载分布的影响规律与接触角相似，负误差更有利于降低前3个螺纹牙承载比例，螺旋升角越大，对前3个滚柱螺纹牙承载分布影响越大.当螺旋升角为2.336 9°时，滚柱螺纹牙承载比为 0.005 4～0.014 6，螺旋升角为 11.532 6°时，滚柱螺纹牙承载比为 0.001 7～0.035 1.可见，螺旋升角较小时，螺纹牙承载分布更加均匀.与此同时，螺旋升角的大小决定了PRSM的直线进给速度，因此，在进行结构参数设计时，应综合考虑速度指标和承载要求.

2.5 滚柱螺纹牙数对承载分布的影响

选取滚柱螺纹牙数分别为5、8、10、15和20，考察其对滚柱螺纹牙承载分布的影响.接触角和螺旋升角分别为 45°和 11.532 6°，负载为50 kN，误差分布和材料弹性模量比不变.计算所得承载分布结果如图7所示.

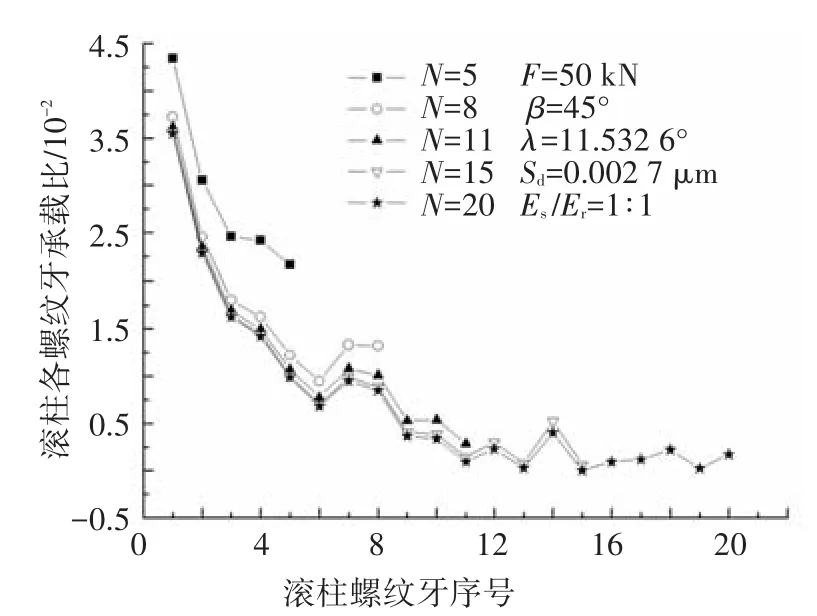
图7 滚柱螺纹牙数对滚柱承载分布的影响

由图7可得，滚柱第1个螺纹牙承载比例最大，随着螺纹牙数的增大，各螺纹牙承载比例逐渐降低，载荷主要集中在前3个螺纹牙上.在本例所取参数条件下，当螺纹牙数＞8时，后面各螺纹牙承载比例基本保持不变，而且误差对承载比例的影响较小，是导致承载波动的主因.由此，在PRSM结构参数设计中，在满足结构承载条件下，应尽量减小滚柱螺纹牙数，因为牙数越多，滚柱结构尺寸越大，使得整个螺母尺寸变大，PRSM总的行程减小，而且螺纹牙接触点越多会产生更多的摩擦损耗和摩擦热，进而降低PRSM的传动效率.

2.6 材料弹性模量比对承载分布的影响

本节假定螺母和丝杠的材料弹性模量相等，考察材料弹性模量比在1∶10和10∶1之间变化时滚柱螺纹牙承载分布规律.负载为50 kN，接触角、螺旋升角、误差分布不变.计算结果如图8.

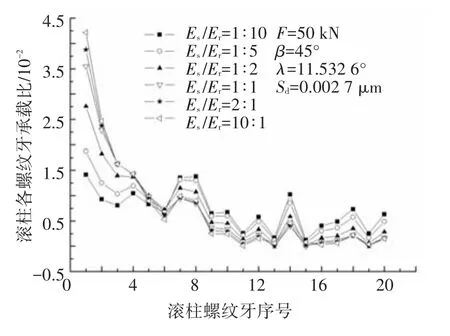
图8 材料弹性模量比对滚柱承载分布的影响

由图8可以看出，在相同误差分布下，随着丝杠(或螺母)弹性模量的增大，滚柱螺纹牙承载分布均匀性变差，第1个螺纹牙承载比例较快增大，且当丝杠(或螺母)弹性模量小于滚柱弹性模量时，前3个螺纹牙承载比例明显下降.因此，在给定误差分布下，降低丝杠(或螺母)弹性模量，特别是保证Es/Er＜1，可有效地改善滚柱螺纹牙承载分布.这是因为丝杠(或螺母)弹性模量刚度降低，丝杠或螺母易于变形，前几个螺纹牙承载分布集中程度降低，可将更多负载传递到后面各螺纹牙.但是，根据PRSM结构特点和传动原理可知，若滚柱和螺母啮合时产生的弹性变形量过大，会导致滚柱相对于螺母发生轴向位移［15］，并产生较大滑动摩擦，最终降低传动效率和位置精度.所以，为了达到改善滚柱螺纹牙承载分布的目的，通常仅在丝杠侧保证Es/Er＜1即可.

3 结论

1)建立了考虑误差影响的PRSM滚柱螺纹牙承载分布计算模型，系统分析了不同负载F、接触角β、螺旋升角λ、滚柱螺纹牙数N和材料弹性模量比Es/Er对滚柱螺纹牙承载分布的影响.

2)在相同误差分布下，负载越小，滚柱螺纹牙承载分布波动越大，而且前3个螺纹牙承载比例相差较大.随着负载增大，各个螺纹牙的承载比例变化减小.

3)接触角和螺旋升角对滚柱螺纹牙承载分布的影响规律相同，随着二者的增大，对前3个滚柱螺纹牙承载分布影响越大.在相同误差分布和负载条件下，接触角和螺旋升角越小，滚柱螺纹牙承载分布相对更加均匀.

4)随着螺纹牙数的增大，各螺纹牙承载比例逐渐降低，载荷主要集中在前3个螺纹牙上，且滚柱第1个螺纹牙承载比例最大.

5)降低丝杠弹性模量，特别是保证Es/Er＜1可有效地改善滚柱螺纹牙承载分布.该分析方法可扩展至考虑丝杠、滚柱和螺母材料均不相同的情况.

［1］MA S J，LIU G，ZHOU J X，et al.Optimal design and contact analysis for planetary roller screw［J］，Applied Mechanics and Materials，2011，86:361-364.

［2］CLAEYSSEN F，JÄNKER P，LELETTY R，et al.New actuators for aircraft，space and military applications［C］//12th International Conference on New Actuators.Bremen:［s.n.］，2010:324-330.

［3］ LISCOUËT J，BUDINGER M，MARE J C，et al.Modelling approach for the simulation-based preliminary design of power transmissions［J］.Mechanism and Machine Theory，2011，46:276-289.

［4］OHASHI Y，ANDRADE A D，NOSÉ Y.Hemolysis in an electromechanical driven pulsatile total artificial heart［J］.Artificial Organs，2003，27(12):1089-1093.

［5］ BRANDENBURG G，BRÜCKL S，DORMANN J.Comparative investigation of rotary and linear motor feed drive systems for high precision machine tools［C］//Proceedingsofthe6th InternationalWorkshop on Advanced Motion Control.Piscataway:IEEE，2000:384-389.

［6］VELINSKY S A，CHU B，LASKY T A.Kinematics and efficiency analysis of the planetary roller screw mechanism［J］.Journal of Mechanical Design，2009，131(1):011016-8.

［7］JONES M H，VELINSKY S A.Contact kinematics in the planetary rollerscrew mechanism［J］.Journalof Mechanical Design，2013，135(5):051003-10.

［8］马尚君，刘更，佟瑞庭.行星滚柱丝杠副摩擦力矩及传动效率研究［J］.哈尔滨工业大学学报，2013，45(11):74-79.

［9］ YOUSEF HOJJAT M，MAHDI A.A comprehensive study on capabilities and limitations of roller-screw with emphasis on slip tendency［J］.Mechanism and Machine Theory，2009，44:1887-1899.

［10］杨家军，韦振兴，朱继生，等.行星滚柱丝杠副载荷分布及刚度计算［J］.华中科技大学学报，2011，39(4):1-4.

［11］JONES M H，VELINSKY S A.Stiffness of the roller screw mechanism by the direct method［J］.Mechanics Based Design of Structures and Machines，2014，42:17-34.

［12］RYS J，LISOWSKI F.The computational model of the load distribution between elements in planetary roller screw［C］//9th International Conference on Fracture ＆Strength of Solids.Jeju:［s.n.］，2013.

［13］MEI X S，MASAOMI T，TAO T，et al.Study on the load distribution ofballscrews with errors［J］Mechanism and Machine Theory，2003，38:1257-1269.

［14］MA，S J，LIU G，TONG R T，et al.A new study on the parameter relationships of planetary roller screws［J］.Mathematical Problem in Engineering，2012，29pages，DOI:10.1155/2012/340437.

［15］JONES M H，VELINSKY S A.Kinematics of roller migration in the planetary roller screw mechanism［J］.Journal of Mechanical Design，2012，134(6):061006-6.