数控车床进给系统基于模糊理论的故障树分析

张义民，肖 洁，李常有

(东北大学机械工程与自动化学院，110004沈阳)

对数控车床进给系统进行可靠性研究是十分必要的，故障树分析是可靠性研究的重要内容，故障树分析把系统的故障与组成系统各部件的故障有机地联系在一起，可以找出系统的全部可能失效状态和薄弱环节［1-5］.目前，国内还没有学者专门针对数控车床进给系统做故障树分析，而故障树分析理论本身，也存在着一些问题，比如底事件概率获取比较困难.文献［6-8］对数控车床做了故障树分析，建立故障树并对其进行定性分析求出最小割集，但未进行定量分析;主要原因是底事件概率获取比较困难.

本文针对ETC36数控车床进给系统建立故障树，并对其进行定性和定量分析，得到进给系统的最可能失效状态和薄弱环节.同时，采用专家语言评价的方法来获取底事件的模糊概率值，由此计算顶事件的模糊概率，并将计算结果与实际值进行对比，验证了此方法的可行性，可以有效地解决故障树底事件概率获取困难的问题.

1 建立故障树

1.1 ETC36数控车床进给系统工作原理

ETC36数控车床的进给系统由伺服系统、电气系统和机械结构系统组成［9］，伺服系统由控制器、传感器等组成，电气系统由步进电机、限位开关和各种导线等组成，机械结构主要有两部分，分为X轴方向进给结构和Z轴方向进给结构，两部分结构差异不大，所以统一考虑，其组成主要有以下几个部件:丝杠、轴承、螺母、滚动导轨、联轴器.步进电机通过弹性联轴器与丝杠相连，丝杠由角接触轴承支撑，步进电机带动丝杠转动，使得套在丝杠上的螺母沿着丝杠轴向运动，带动与螺母固定的工作台移动，工作台支撑在滚动导轨上.其机械结构简图如图1所示.

1.2 建树

顶事件为进给系统故障，分为不能进给和不能准确进给.按其组成结构，分为伺服系统、电气系统和机械结构故障.伺服系统故障由驱动器故障和传感器故障引起;电气故障由行程开关故障和伺服电机故障引起;机械故障，按其组成结构，分为联轴器、滚珠丝杠、导轨、支撑轴承等部位的故障，将其定为机械结构故障下的中间故障类型;再下一级定为底事件.所建故障树如图2:(其中T为顶事件，M开头为中间事件，X开头为底事件).

图1 进给系统示意图

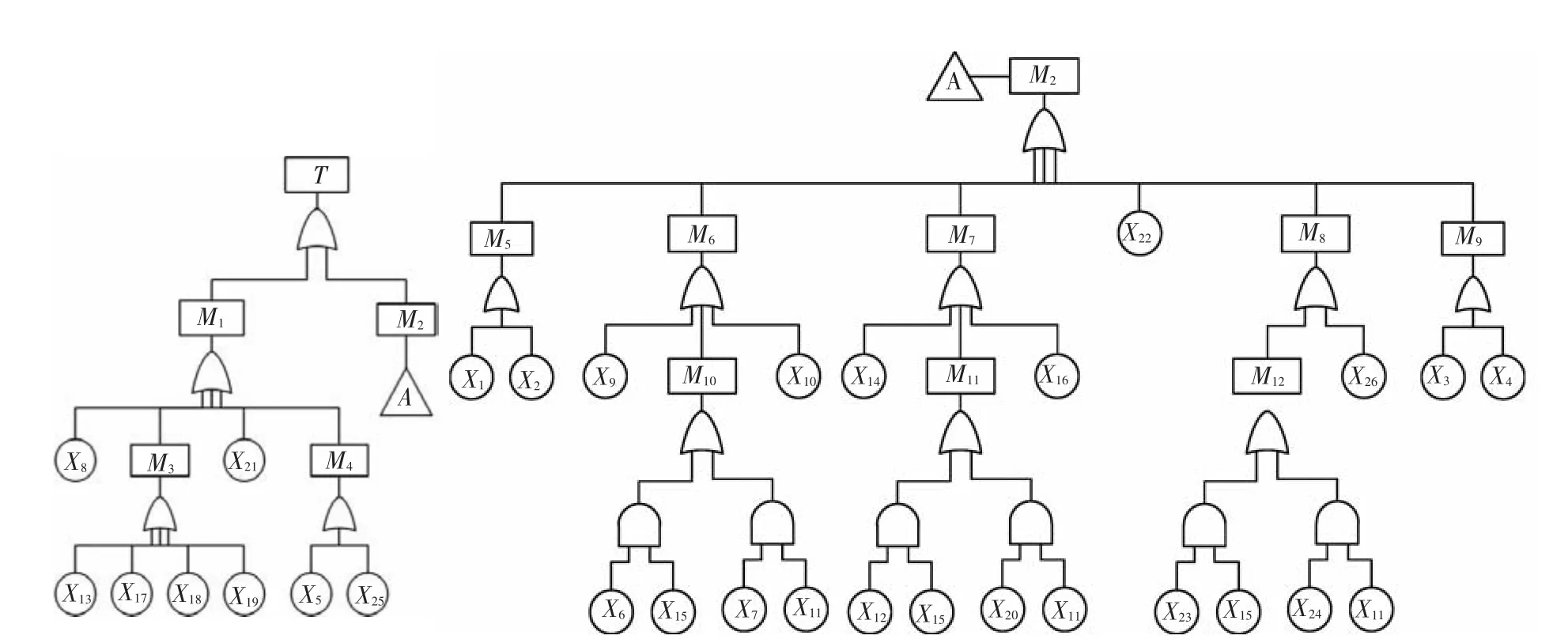
图2 数控车床进给系统故障树

2 定性分析

定性分析就是找出最小割集，在故障树中，割集是能使顶事件发生的一些底事件的集合，如果割集中的任一底事件不发生，顶事件也就不发生，这样的割集称之为最小割集［10］.本文所建的故障树，要求最小割集，根据与门用乘、或门用加的原则，有

简化得

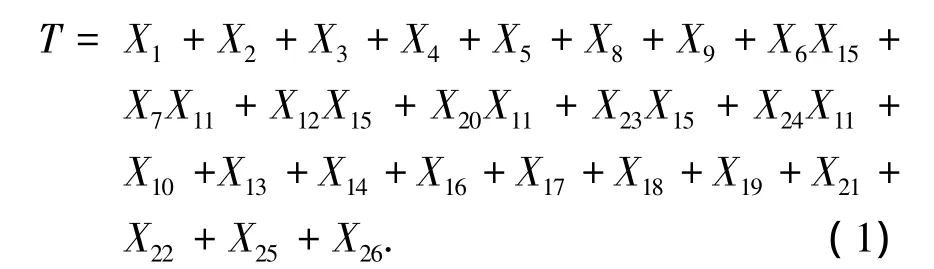
由式(1)可得24个最小割集:{X1}，…，{X26}.代表ETC36数控车床进给系统的24种失效模式.

3 定量分析

3.1 底事件模糊概率值确定

由于底事件没有具体统计数据，在没有试验验证的前提下，可以根据生产一线故障专家的经验判断，将底事件发生的概率用语言描述，分7个等级，分别是非常低、低、较低、中等、较高、高、非常高.沈阳机床ETC36数控车床各类型零件的设计可靠性在0.99以上，而底事件均是各类零件的故障，所以底事件的发生概率理论上＜0.01.假设底事件发生的概率为0～0.02，7个等级所对应的概率 分 别 为 0 ～ 0.000 1、0.000 1 ～ 0.000 5、0.000 5～ 0.001、0.001 ～ 0.003、0.003 ～ 0.005、0.005～0.010、0.01～0.02.对每个底事件，由 3 位专家给出评价，然后综合3位专家的意见，给出参考概率.通过沈阳机床生产一线专家对底事件的评价，得到底事件的语言描述和参考概率如表1所示.

表1 专家语言评价表

参考概率不是真实概率，可能会偏离真实概率，但偏离的程度无从得知，为简化计算，假定与真实概率的偏差不超过30%，将参考概率值简化成三角型模糊数，三角型模糊数可表示为

其中m为参考概率值，底事件的模糊概率值都可以用这种方式表示，用于后面的计算.

3.2 顶事件模糊概率计算

三角型模糊数的隶属函数为(λ为置信水平)

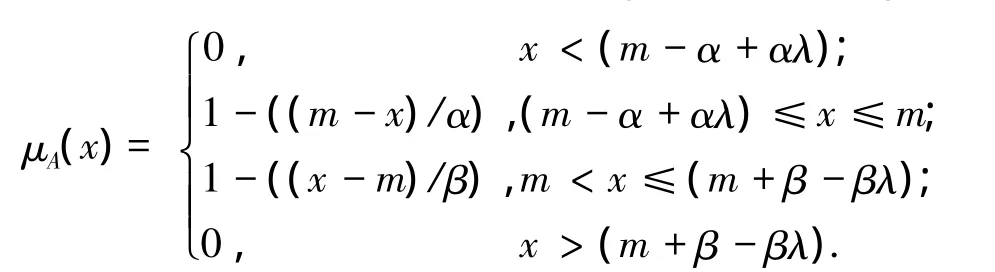
在模糊故障树分析［11-12］过程中，采用模糊数来描述底事件发生的概率，用模糊算子代替传统的逻辑门算子，从而得到顶事件发生的概率模糊数.当用三角型模糊数表示底事件发生概率时，根据三角型模糊数表示方法，设Fiλ为第i个底事件发生的模糊概率，结合式(2)，则故障树的与门结构和或门结构的模糊算子Fandsλ、Forsλ分别为

由求最小割集的式(1)可知，每一个最小割集发生都能导致顶事件发生，最小割集发生的概率用与门结构公式计算，顶事件发生的概率用或门结构计算公式.设各最小割集X1，X2，…，X26发生的概率为PX1，PX2，…，PX27顶事件发生的概率为PT，则

应用式(1)～(4)并将表2的数据代入，可求得顶事件的模糊概率值为

3.3 理论计算与实际数据的对比分析

根据沈阳机床提供的部分ETC36使用信息，得知2013年共售出此类型机床957台，在使用过程中出现各类型故障的有327台，其中与进给系统有关的故障占30%，从而可推断出在使用过程中进给系统的故障概率为10.3%，

而理论计算的进给系统模糊概率值由式(5)给出:式(5)意义表示当置信度为λ时，概率区间为:［0.081 7+0.031 7λ，0.144 3-0.033 7λ］，所以根据上述理论计算得到了ETC36数控车床进给系统在使用过程中的失效概率为［0.081 7+0.031 7λ，0.144 3-0.033 7λ］.

经计算，当置信度λ在0.70这个水平时，模糊概率区间正好包含10.3%，表明理论计算与实际相符得比较好，也能证实故障树建立的正确性和专家语言评价法的可行性.

3.4 底事件模糊重要度分析

底事件的模糊重要度为［13］

计算得到各底事件的模糊重要度见表2.

表2 底事件模糊重要度列表

由表2可知，模糊重要度比较大的几个底事件为:X1、X8、X9、X11、X13、X16，这几个底事件是对系统故障概率贡献最大的，也是系统的薄弱环节，它们分别是行程开关故障、轴承预紧不当、轴承疲劳、未及时维护润滑、滚珠丝杠预紧不当、滚珠丝杠副接触疲劳.

4 结论

1)首次将故障树分析应用到ETC36数控车床进给系统的故障分析中，并通过定性分析得到故障树的24个最小割集.即ETC36数控车床进给系统的24种失效模式.

2)在ETC36数控车床进给系统可靠性试验和故障数据缺失的情况下，尝试采用专家语言评价的方法，应用于故障树分析，获得底事件的模糊概率值，并应用于定量分析，计算出 ETC36数控车床进给系统的失效概率的模糊值.

3)将理论计算与实际数据相对比，得到相应的置信度水平λ=0.70，这个值可以为ETC36数控车床其他系统的故障分析提供参考价值.

4)通过理论分析和实际对比找出了引起ETC36数控车床进给系统失效的薄弱环节，为降低ETC36数控车床故障概率提供了理论和实际依据.

［1］FERDOUS R，KHAN F，SADIQ R，et al.Fault and event tree analyses for process systems risk analysis:uncertainty handling formulations［J］.Risk Analysis，2011，31(1):86-107.

［2］BOUDALI H，DUGAN J B.A discrete-time Bayesian network reliability modeling and analysis framework［J］.Reliability Engineering＆ System Safety，2005，87(3):337-349.

［3］ SHU M H，CHENG C H，CHANG J R.Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly［J］.Microelectronics Reliability，2006，46(12):2139-2148.

［4］CHENG S R.Fault-tree analysis for liquefied natural gas terminal emergency shutdown system ［J］.Expert Systems with Applications，2009，36(9):11918-11924.

［5］KUMAR M，YADAV S P.The weakest t-norm based intuitionistic fuzzy fault-tree analysis to evaluate［J］.ISA Trans，2012，51(4):531-538.

［6］WANG C，XING L，AMARI S V.A fast approximation method for reliability analysis of cold-standby systems［J］.Reliability Engineering ＆ System Safety，2012，106:119-126.

［7］于捷.CAK系列数控车床 FTA分析［J］.长春大学学报，2000，10(4):3-5.

［8］周磊，陈时锦，梁迎春，等.基于失效树分析的机床进给系统可靠性设计［J］.机械设计与制造，2007(6):60-62.

［9］张英芝，申桂香，薛玉霞，等.数控车床主轴模糊故障树分析［J］.吉林大学学报，2006，36(S2):65-68.

［10］HUANG H，ZHANG Z H，LI Y F.A new ordering method of basic events in fault tree analysis［J］.Quality and Reliability Engineering International，2012，28(3):297-305.

［11］DONG Y，YU D.Estimation of failure probability of oil and gas transmission pipelines by fuzzy fault tree analysis［J］.Journal of Loss Prevention in the Process Industries，2005，18(2):83-88.

［12］LONG W，SATO Y，HORIGOME M.Quantification of sequential failure logic for fault tree analysis［J］.Reliability Engineering ＆ System Safety，2000，67(3):269-274.

［13］宋保维.系统可靠性设计与分析［M］.西安:西北工业大学出版社，2008:136-137.