大规模环境下基于图优化SLAM的后端优化方法
王忠立,赵 杰,蔡鹤皋
(1.北京交通大学电子信息工程学院,100044北京;2.机器人技术与系统国家重点实验室(哈尔滨工业大学),150080哈尔滨)
随着移动机器人的应用逐步从小规模、静态环境向大规模环境发展,基于图优化的SLAM方法成为研究热点.从实现框架上,可以将SLAM分解为前端的图构建和后端的图优化两个过程.相对于早期的基于递归贝叶斯状态估计理论方法,如基于Kalman滤波和基于粒子滤波(PF)的方法,图优化SLAM方法是先通过前端的图构建过程得到初始状态估计,然后在后端对初始状态估计进一步优化求解,因此地图的一致性和精度更好.基于图优化的SLAM方法是一种batch方法.在文献[1]中,详细介绍了图优化建模方法及前端的数据关联和环形闭合检测方法.本文主要对基于图优化SLAM的后端优化方法进行总结.
在前端图构建得到的“初始图”中,由于传感器的噪声、系统参数的不确定性、环形闭合检测的误差乃至错误等因素,使得图优化过程具有很大的挑战性.不仅要求优化方法具有较好的鲁棒性、稳定性,同时,优化过程通常是对整个地图进行的,在大规模环境下,也要考虑优化方法的计算复杂度问题.国内外学者提出了各种优化计算方法,主要包括:基于最小二乘法的优化方法,基于松弛迭代的优化方法,基于随机梯度下降的优化方法,以及基于流形的优化方法等.并对基于图优化SLAM的计算效率、鲁棒性和可扩展性等方面展开了研究.但对算法的性能及地图重建结果评估的研究相对较少.针对大规模环境下的地图创建,地图创建质量的评估也是非常重要的一环.为此,本文对两种地图质量评价方法进行了总结,对优化方法存在的挑战性进行了阐述,在文献[2]基础上,介绍了最新的研究进展,并对发展趋势进行了展望.
1 基于图优化SLAM的后端优化方法
1.1 优化方法概述
基于图优化的SLAM方法,是利用图模型对SLAM问题进行建模.模型中的节点对应不同时刻机器人及环境组成系统的状态,边则描述了系统状态(节点)之间的约束关系[3].这类方法将SLAM问题划分为前端(front-end)和后端(backend)两个部分,如图1所示.前端完成图的构建,即根据观测和系统约束构建图的节点和边;后端主要完成图的优化.基于图优化的方法利用所有的观测信息来优化估计机器人完整的运动轨迹,因此也称为全SLAM方法.
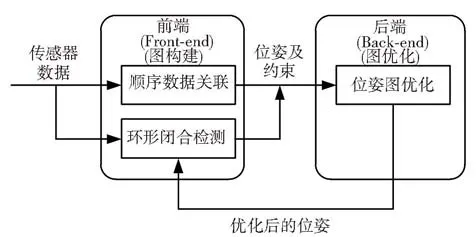
图1 基于图优化的SLAM框架
在前端部分,顺序数据关联是指相邻观测数据帧间的匹配及相对姿态估计问题,而环形闭合检测则根据观测数据判断机器人是否处在之前已访问过的环境中.二者的核心是要解决数据关联问题,前者考虑局部数据关联,而后者则涉及全局数据关联.顺序数据关联与环形闭合检测都是根据观测信息建立图节点间的约束,即完成图的构建,是基于图优化方法前端的两个核心部分.
由于观测噪声以及数据关联误差的存在,前端得到的图往往存在不一致性.若用Ti来表示数据帧间的相对变换矩阵,而且T0,T1,…,Tn构成一个闭环,则理想情况下,应满足:
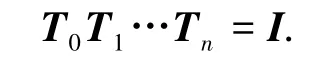
式中Ⅰ为单位矩阵.但通过观测信息关联得到的相对变换矩阵通常不满足该约束.在基于图的模型描述中,机器人的位姿是待估计的随机变量,位姿间的约束则是与随机变量相关的观测,图优化结果对应于位姿的最大似然估计.与顺序数据关联及环形闭合检测不同,图优化部分一般不直接处理观测数据,而是在前端构造的图基础上进行优化运算.
Golfarelli等[4]将图优化视为质量-弹簧模型,从另一个视角来解释图的优化问题,如图2所示.在该模型中,将机器人的位姿看作是带质量的节点(黑色圆点),而约束则看作是连接这些节点的弹簧.由于每个约束都是根据与之相关的观测独立求解的,它们之间存在不一致性,此时弹簧处在受力形变状态,这样的物理系统通常并不稳定.当弹簧对质点的作用力使系统重新达到平衡时,系统处在能量最小状态,此时质点的分布即代表最优的位姿序列.弹簧的系数通过观测的不确定性来(协方差)表示.观测的不确定性越小,弹簧的强度越大,使其形变需要的外部作用力也越大;反之,观测的不确定性越大,弹簧的强度越小,使其形变需要的外部作用力也就越小.系统的能量最小状态对应于非线性最小二乘问题的最优解.
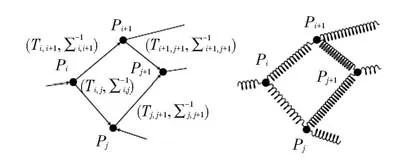
图2 基于图优化的mass-spring模型
基于图优化SLAM的后端优化方法,概括起来可以分为基于最小二乘法的优化方法,基于松弛迭代的优化方法,基于随机梯度下降的优化方法,以及基于流形的优化方法等.
1.2 基于最小二乘法的优化方法
SLAM可以看作是一个非线性最小二乘问题[5].基于最小二乘的优化方法是通过对目标函数的一阶泰勒展开对系统进行线性化,采用迭代法求解线性系统的解,如 Gauss-Newton方法、Levenberg-Marquardt方法等.如果不考虑SLAM问题的稀疏结构特性并假定图中的节点数为n,则Levenberg-Marquardt算法的时间复杂度为O(n3)[6],在实际问题求解中远不能满足实时性要求[7].Dellaert和 Kaess[5]提出利用 SLAM 问题中内在的稀疏结构特性,通过稀疏矩阵分解(如稀疏Cholesky分解等)来求解的非线性最小二乘的方法.Kaess等[8]将图建模和稀疏线性代数方法相结合,提出了iSAM方法,iSAM是增量式图优化方法的代表.该方法通过对平滑信息矩阵作QR分解,并选择性对其进行增量式更新,从而避免了每次重新计算平滑信息矩阵,提高了更新的效率,处理问题的规模也大大增加,其最佳复杂度为O(n).在iSAM的基础上,通过节点的重新排序和重新线性化,Kaess等[9]又提出了改进后的iSAM2方法.为了进一步提高增量式更新过程的计算效率,Kaess等[10]在 iSAM2的框架下,提出采用贝叶斯树结构来描述SLAM的方法.在SLAM稀疏特性的研究方法上,Konolige等[11]提出一种根据给定图约束快速构造稀疏矩阵的SPA(sparse pose adjustment)方法.
1.3 基于随机梯度下降法的优化方法
Olson等[7]将随机梯度下降方法应用到位姿图SLAM的优化中.每次迭代时随机选取图中的一条边作为当前约束并计算相应的梯度下降方向,然后在该方向上对目标函数寻优.随机梯度下降方法具有不易陷入局部极值的优点,对初始值具有较高的鲁棒性.实验证明,即使初始值与最优值相差较远,甚至在全零初始值或随机初始值时,随机梯度下降方法也能取得较好的收敛结果.Grisetti等[12]对Olson等所提的方法进行了改进和拓展,采用树型结构来描述位姿间的关系并通过增量方式表示待求解的状态,从而能更有效地对位姿进行更新.Grisetti等[13]还将树型结构表示以及随机梯度方法应用到6自由度位姿的优化中,提出了基于树的网络优化(TORO)方法.
1.4 基于松弛的优化方法
Duckett等[14]提出采用 Gauss-Seidel松弛方法实现后端优化.其基本思想是依次选取每个节点,根据其相邻节点的位置及它们之间的约束关系重新计算并更新该节点的位置,且每次迭代都遍历所有节点.在假定方位角已知(如通过电子罗盘测量)的情况下,Duckett等证明了其必收敛于最优解.该方法可用于增量式的SLAM中,在每次有新的观测到来时直接在原来结果基础上进行更新.该方法的缺陷是,当某条边的误差较大时,需要多次迭代才能将误差分配到其他边中,而这正是出现环形闭合时所需要应对的情况.Frese等[15]提出多层次松弛的优化策略,并利用多重网格方法求解偏微分方程,从而大大地提高了出现环形闭合时节点的优化更新效率.
1.5 流形优化
以上三类优化方法均假定优化过程是在欧氏空间中进行的.在欧式空间中,机器人位姿中的旋转分量的估计可能会出现奇异.为了避免奇异值问题,旋转分量部分可以采用四元数法表示,但又产生了额外的自由度,引入不必要的误差.为此,Grisetti等[16]提出在流形空间中进行优化的思想,避免状态空间参数化时可能出现的奇异值问题,提出了一种分层优化的图优化技术(即HOGMAN方法).该方法在在线建图过程中,根据当前的观测约束,对地图的修正只在上层(粗略描述层)进行,从而提高了效率.最近,研究者们提供了能用于流形优化的开源工具(g2o).Kummerle等[17]将HOG-MAN方法和Konolige等人提出的SPA思想结合起来,提出了基于流形的图优化通用框架(g2o框架),大大提高了开发效率.在g2o框架的基础上,Kummerle等[18]进一步扩展了状态空间,如增加描述可能随时间变化的系统参数,从而可实现同步传感器标定、建图和机器人定位任务的方法.Hertzberg[19]和 Wagner[20]等也将流形方法扩展到传感器的融合和标定问题中,取得了初步成果.
1.6 图优化的计算效率、鲁棒性和扩展性
非线性最小二乘法的一个不足是对初始值的依赖,如果给定的初始值离最优解距离远,则很容易陷入局部极值点.为此,Carlone等[21]提出对基于图优化的SLAM作线性近似并给出解析求解的方法,可以利用其结果作为非线性最小二乘方法的初始值.但目前该方法只适用于2D SLAM.针对非线性最小二乘法对异常点的鲁棒性不好的特点,目前已有多种解决方法.Sunderhauf等[22]提出了允许在图优化的过程中改变图的拓扑结构以剔除错误的环形闭合,从而提高了方法的鲁棒性.在随机梯度下降法(SGD)和Levenberg-Marquardt方法的基础上,提出了前置滤波SGD和前置滤波Levenberg-Marquardt方法,二者均是在优化操作之前,利用一个前置滤波器来完成一些预处理过程,以确保全局一致性.这些方法的应用使得非线性最小二乘法的鲁棒性有所提高.
当机器人在大小固定的环境中行走时,图的节点数目应该跟环境的规模大小相关,而不是与机器人运动轨迹的长度相关.因此,要使SLAM方法具备良好的扩展性,关键是对图节点进行有效的控制.减少节点数最为直观的方法是对节点间的距离进行限制,即只有节点间的距离超过一定的阈值时才添加到图中[23].Kretzschmar 等[24]从观测所含的信息出发,评估观测帧的信息增益,并依此对图进行剪枝,以控制节点数目.该方法在保持节点规模的同时具有最小的信息损失,因而也保证了地图信息的完整性.对节点进行剪枝实际对应节点的边缘化过程,这可能导致图的结构变得密集.Kretzschmar等[25]提出采用 Chow-Liu 树对节点间的关系作近似描述,以保证节点连接的稀疏性.Yasir和 Jose等[26]提出利用线段拟合机器人的运动轨迹,从而减小位姿图规模的方法.Xiang等[27]提出一种变分辨率的地图表示方法.
上述研究方法进一步提高了基于图优化方法的计算效率、鲁棒性和可扩展性.基于图优化的增量式SLAM方法目前研究最广泛.
2 地图质量的评价
由于SLAM问题的复杂性,其结果是多方面综合,因此要给出一个大而全的评价方法是很困难的.比较合理的方法就是对SLAM的各个子问题分别给出评价的方法.尽管如此,要对一些子问题进行评价也是非常困难的,像视觉领域中对立体视觉算法的评估一样[28-29],因为这些子问题本身也很复杂.另外,对于大规模环境下的地图重建结果进行评估时,目前可用于对比分析的数据集也很有限.有学者提出了一些通用的数据集[30-31],但用于性能对比时,由于这些数据集最初不是用于对比的目的,因此很多没有真实数据.这也是目前进行评估时存在的困难之一.
Olson等[32]对地图优化算法的评估方法进行了研究,提出要对全局优化(Batch模式,通常是离线的)和在线优化分别进行比较.
在假定前端的特征提取、匹配(包括环形闭合检测)以及异常点已经排除的前提下,地图优化实质是后验概率估计问题.目前主要有两种方法:基于χ2误差和基于均方差(MSE)的评价方法.
2.1 基于χ2误差和均方差的评价方法比较
研究表明,基于χ2误差方法的局限性在于:χ2误差小的地图优化结果不一定比χ2误差大的更好[33].如图3所示,是两种不同误差定义方法的优化仿真结果比较.图3(a)是真实值,通过对比图3(b)和图3(c)可见,在图3(b)中的χ2误差很小,但却远远偏离真实值,而图3(c)的χ2误差虽然很大,但却更接近真实值.
在地图优化问题上,产生如图3所示结果的主要原因是由于观测过程具有高度非线性本质,造成优化曲面非常复杂.某些情况下,映射问题产生的优化曲面有“浅谷”出现,在此处,优化表面变化大,但对χ2误差的影响却很小.即基于χ2误差的优化目标函数定义中,机器人位姿估计和地图特征点位置估计相互耦合的关系在某种程度上抵消了相互误差对地图结果的影响.图3(b)中特征点的位置和机器人的位姿在优化过程中同时发生了偏离,而χ2误差很小.
由此可见,在大规模环境地图创建中,误差函数的定义非常关键.常用的基于观测的误差定义方法(χ2误差)有时不一定很有效.基于MSE的误差定义能得到较好的结果.
2.2 过拟合(over-fitting)问题
在机器学习中,为了得到一致假设而使假设变得过于复杂,在训练数据上能够获得比其他假设更好地拟合,但是在训练数据外的数据集上,却不能很好地拟合数据,出现了过拟合现象.出现这种现象的主要原因是训练数据中存在噪声或者训练数据太少.在地图优化估计时,如果平均节点度(average node degree)小会出现该问题.如图4所示,机器人沿着一个方格运动,在右下角的区域,由于节点度小,存在过拟合问题,导致地图优化结果和实际情况的不一致.解决过拟合问题的方法主要有两种:提前停止树的增长或者对已经生成的树按照一定的规则进行后剪枝.

图4 过拟合问题
3 发展趋势
近年来,SLAM的研究也出现一些新的趋势:
1)随着移动机器人的工作环境从室内到室外的扩展,工作空间越来越大,面临的环境也越来越复杂.相对于室内较为简单的环境对象,室外环境由各种对象组成,有静止的、移动的,有行人、各种车辆等.如何实现复杂、大规模、动态环境下地图表示,高精度、高效率的地图创建,以及移动机器人的自定位是一个很有挑战性的研究课题,是现阶段SLAM问题研究的重点.
2)对终生地图创建(lifelong mapping)和维护的研究.在传统意义上,机器人一旦通过SLAM实现了未知环境的建图,则建图任务结束,机器人即可利用已经建好的地图进行定位或运动规划.终生地图研究将机器人长期置于未知环境中,因此需要应对环境的变化,并持续对地图进行更新、维护.这种对地图的不断更新、维护就构成了终生地图研究的主要内容[33].
3)语义地图(Semantic map)创建的研究.为了使机器人具备理解场景以及能够识别场景物体的能力,构造具有语义信息的地图是一种重要途径.构建语义地图,可使机器人能够更好地为人类提供服务,是SLAM发展的趋势之一.
4)基于多传感器融合的SLAM研究.通过多传感器信息融合,可以弥补单一传感器在数据获取时的不足,降低状态估计的不确定性,改善数据关联、环闭检测等关键环节的精度和可靠性,进而提高机器人定位和环境建图的精度.多传感器融合在移动机器人SLAM中的研究和应用将会越来越多.
5)多机器人协作 SLAM研究.与单机器人SLAM相比,多机器人SLAM问题涉及多几个机器人得到的子图如何拼接得到全局地图,以及在全局地图中各个机器人的定位问题.多机器人协作完成SLAM具有更准确、更高效率的优势,因此受到越来越多的关注,正成为一个热点研究问题.
6)非欧式空间下的建模与状态估计方法.针对SLAM问题,在欧式空间中对机器人的位姿进行求解存在奇异值问题.另外,目前大多数SLAM方法是基于传感器空间的,但机器人控制,需要将机器人坐标系和传感器坐标系之间关联考虑,如在基于激光扫描的传感器中,利用里程计获取的运动信息,是在机器人坐标系下描述,和观测传感器(激光扫描)是不同的坐标系,二者的变换关系是假定准确已知的.虽然可以通过标定得到二者变换关系,但结果也有不确定性,不确定性对SLAM结果的影响目前还未知.Grisetti等[16]提出在流形空间中进行优化的思想,其实质是将SLAM问题置于一个高维空间中,不仅可以避免状态空间参数化时可能出现的奇异值问题,还可以将传感器自身参数的在线估计等问题统一到一个完整的系统框架下.对非欧式空间中的求解方法的讨论,将对SLAM的发展产生深刻的影响.
[1]王忠立,赵杰,蔡鹤皋.大规模环境下基于图优化SLAM的图构建方法[J].哈尔滨工业大学学报,2015,47(1):75-85.
[2]梁明杰,闵华清,罗荣华.基于图优化的同时定位与地图创建综述[J].机器人,2013,35(4):500-512.
[3]GRISETTI G,KUMMERLE R,STACHNISS C,et al.A tutorial on graph-based SLAM[J].IEEE Transaction on Intelligent Transportation Systems Magazine,2010,2(4):31-43.
[4]GOLFARELLI M,MAIO D,RIZZI S.Elastic correction of dead-reckoning errors in map building[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway:IEEE,1998:905-911.
[5]DELLAERT F,KAESS M.Square root SAM:simultaneous localization and mapping via square rootinformation smoothing[J].International Journal of Robotics Research,2006,25(12):1181-1203.
[6] FRESE U,LARSSON P,DUCKETT T.A multilevel relaxation algorithm for simultaneous localization and mapping[J].IEEE Trans on Robotics,2005,21(2):196-207.
[7] OLSON E,LEONARD J,TELLER S.Fast iterative alignment of pose graphs with poor initial estimates[C]//IEEE International Conference on Robotics and Automation.Piscataway:IEEE,2006:2262-2269.
[8]KAESS M,RANGANATHAN A,DELLAERT F.iSAM:Incremental smoothing and mapping[J].IEEE Trans on Robotics,2008,24(6):1365-1378.
[9] KAESS M,JOHANNSSON H,ROBERTS R,et al.iSAM2:incremental smoothing and mapping with fluid relinearization and incremental variable reordering[C]//Intl Conf on Robotics and Automation(ICRA).Shanghai:IEEE,2011:3281-3288.
[10]KAESS M,JOHANNSSON H,ROBERTS R,et al.iSAM2:incremental smoothing and mapping using the bayes tree[J].InternationalJournalofRobotics Research,2012,31(2):216-235.
[11]KONOLIGEK, GRISETTIG, KUMMERLER.Efficient sparse pose adjustment for 2D mapping[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway:IEEE,2010:22-29.
[12]GRISETTI G,STACHNISS C,GRZONKA S,et al.A tree parameterization for efficiently computing maximum likelihood maps using gradient descent[C]//Robotics:Science and Systems III.Cambridge:MIT Press,2008:65-72.
[13]GRISETTI G,STACHNISS C,GRZONKA S.TORO-tree-based network optimizer[CP/OL].[2014-03-15].http://www.openslam.org/toro.html.
[14]DUCKETT T,MARSLAND S,SHAPIRO J.Learning globally consistentmaps by relaxation[C]//IEEE International Conference on Robotics and Automation.Piscataway:IEEE,2000:3841-3846.
[15]FRESE U,LARSSON P,DUCKETT T.A multilevel relaxation algorithm for simultaneous localization and mapping[J].IEEE Trans on Robotics,2005,21(2):196-207.
[16]GRISETTI G,KUMMERLE R,STACHNISS C,et al.Hierarchical optimization on manifolds for online 2D and 3D mapping[C]//IEEE International Conference on Robotics and Automation.Piscataway:IEEE,2010:273-278.
[17]KUMMERLE R,GRISETTI G,STRASDAT H,et al.g2o:A general framework for graph optimization[C]//IEEE International Conference on Robotics and Automation.Shanghai:IEEE,2011:3607-3613.
[18]KUMMERLE R,GRISETTI G,BURGARD W.Simultaneous calibration, localization, and mapping [C]//InternationalConference on IntelligentRobots and Systems.Piscataway:IEEE,2011:3716-3721.
[19]HERTZBERG C,WAGNER R,FRESE U,et al.Integrating generic sensorfusion algorithms with sound state representations through encapsulation of manifolds[J].Information Fusion,2013,14(1):57-77.
[20]WAGNER R,BIRBACH O,FRESE U.Rapid development of manifold-based graph optimization systems for multisensor calibration and SLAM [C]//IEEE/RSJ InternationalConference on IntelligentRobots and Systems.Piscataway:IEEE,2011:3305-3312.
[21]CARLONE L,ARAGUES R,CASTELLANOS J A,et al.A first-order solution to simultaneous localization and mapping with graphical models[C]//IEEE International Conference on Robotics and Automation.Shanghai:IEEE,2011:1764-1771.
[22]SUNDERHAUF N,PROTZEL P.Towards a robust back-end for pose graph SLAM[C]//IEEE International Conference on Robotics and Automation(ICRA),Minnesota:IEEE,2012:1254-1261.
[23]KONOLIGE K,AGRAWAL M.Frame SLAM:from bundle adjustment to real-time visual mapping[J].IEEE Trans on Robotics,2008,24(5):1066-1077.
[24]KRETZSCHMAR H,GRISETTI G,STACHNISS C.Lifelong map learning for graph-based SLAM in static environments[J].Kunstliche Intelligenz,2010,24(3):199-206.
[25]KRETZSCHMAR H,STACHNISS C,GRISETTI G.Efficient information theoretic graph pruning for graphbased SLAM with laser range finders[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway:IEEE,2011:865-871.
[26]YASIR L,JOSE N.Go straight,turn right:pose graph reduction through trajectory segmentation using line segments[C]//European Conference on Mobile Robots(ECMR).Barcelona:IEEE,2013:144-149.
[27]XIANG J,TAZAKI Y,INAGAKI S.Autonomous variable-resolution map building for mobile robots in unknown environments[J].Electeical Engineering in Japan,2014,186(4):59-69.
[28]SCHARSTEIN D,SZELISKI R,HIRSCHMOULLER H.Middlebury stereo vision page[DB/OL].[2014-03-10].http://vision.middlebury.edu/stereo/.
[29]SCHARSTEIN D,SZELISKI R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[C]//IEEE Workshop on Stereo and Multi-Baseline Vision.Hawaii:IEEE,2002:131-140.
[30]HOWARD A,ROY N.The robotics data set repository(Radish)2003[DB/OL].[2014-03-10].http://www.lib.uts.edu.au/data-archive/4843/radish-roboticsdata-set-repository.
[31]NEWMAN P,CORKE P.Editorial:data papers-peer reviewed publication of high quality data sets[J].International Journal of Robotics Research,2009,28(5):587.
[32]OLSON E,KAESS M.Evaluating the performance of map optimization algorithm[EB/OL].[2014-03-20].http://april.eecs.umich.edu/pdfs/olson2009rss.pdf.
[33]KRETZSCHMAR H,GRISETTI G,STACHNISS C.Lifelong map learning for graph-based SLAM in static environments[J].Kunstliche Intelligenz,2010,24(3):199-206.

