弹簧参与的微小振动一定是简谐运动吗

郭 敏 闫诚实 王靖淇 崔景凤 戴 瑞

（1东北师范大学物理学院，吉林长春 130024；2沈阳市第四中学，辽宁沈阳 110023）

1 简谐运动的充要条件

在一维情况下，振子系统的位置可用单一坐标变量x来表示，设任意系统的势能为U＝U（x），受力为f＝f（x），若x0为稳定平衡位置，则有

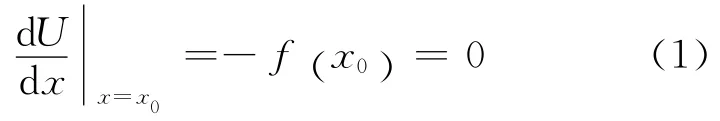
一般情况下，在平衡位置附近（Δx＝x-x0极小），可以将势能函数展开为泰勒级数［1］：

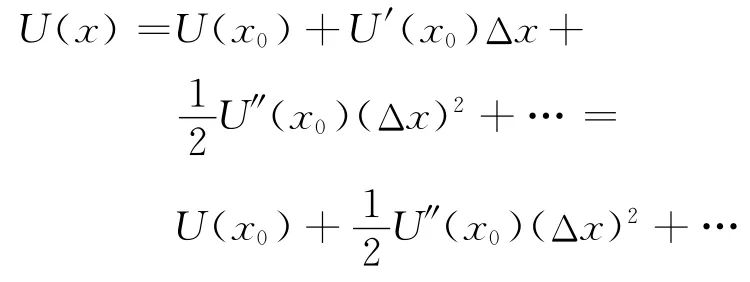
当Δx→0时，若忽略高阶无穷小，则

根据机械能守恒定律有

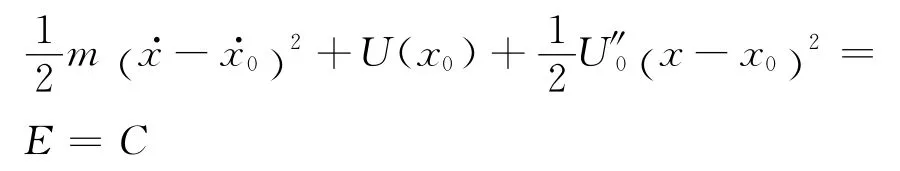
两侧同时对时间求一阶导数有

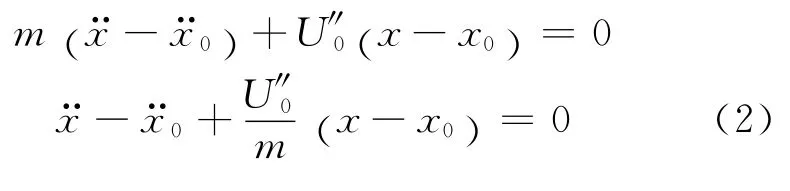
若

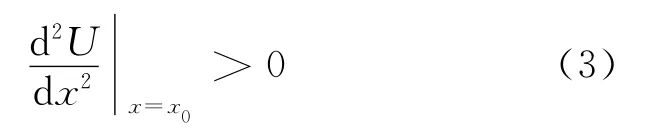
此时系统势能为极小值.

需要说明，当式（3）不成立时，如果势能对位置的高阶变化率满足大于零，即那么x0处也是系统的稳定平衡位置，但此时f（x）可能不再满足f（x）＝-kx这种形式，这样的振动也就一定不是简谐运动了［4］.

2 弹簧参与的微小振动

例1如图1所示，一个原长为l劲度系数为k的弹簧，将其一端固定，另一端连接质量为m中心穿有小孔的质点小球，小球套在光滑的水平细刚性杆上，刚性杆到弹簧固定端的距离刚好等于弹簧的原有长度l.以平衡位置为坐标原点O，建立如图所示坐标轴Ox.外力作用下，小球偏离平衡位置，静止于x处，某一时刻，突然撤去外力，系统沿光滑的水平刚性细杆作微小振动［5］.

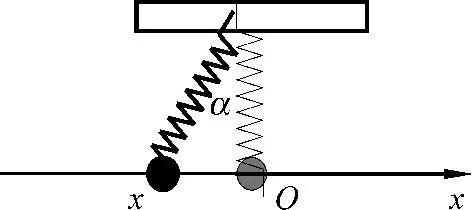
图1 套在水平刚性细杆上的弹簧振子

系统的弹性势能可以表示为

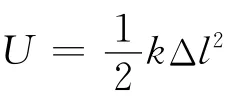
弹簧的伸长量为

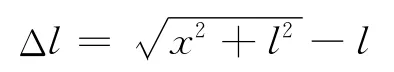
由于小球的横向位移x≪l，将势能在x＝0处展开有

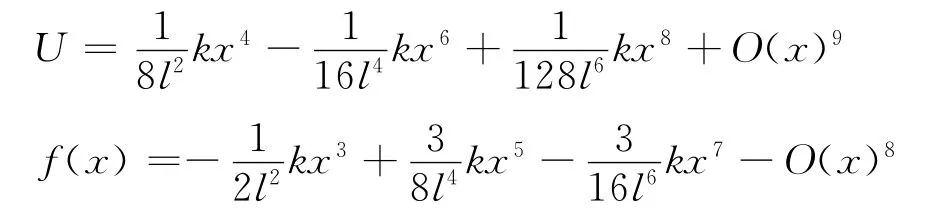
例2光滑水平面上一个质点小球连接两个原长均为l、劲度系数均为k的弹簧，将弹簧的另外两端分别固定，使弹簧处于原长，并与质点小球在同一直线，以平衡位置为坐标原点O，建立如图2（a）所示的坐标轴Ox.在外力作用下，小球偏离平衡位置，如图2（b）所示，静止于x处，某一时刻，突然撤去外力，系统将在光滑平面上沿x方向作微小振动［6］.

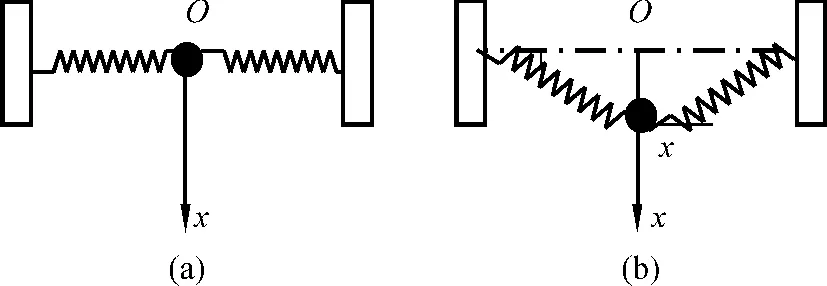
图2 两个弹簧相连的系统

系统的势能为

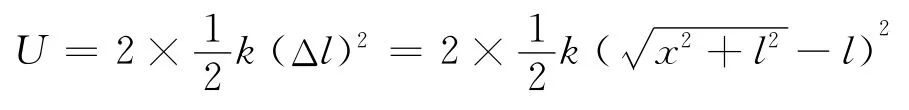
进行泰勒级数展开得

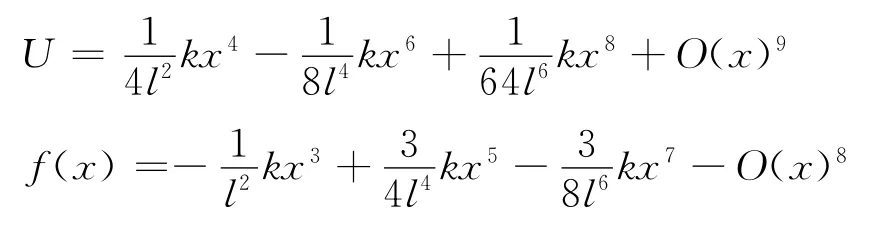
例3若在例2的基础上再加一个弹簧，3根劲度系数为k，原长为l的弹簧互成120°就得到如图3所示的系统，平衡时各弹簧均恰好为原长.以平衡位置为坐标原点O，建立如图所示的坐标轴Ox.在外力作用下，质点小球沿图中Ox轴方向偏离平衡位置，静止于x处，某一时刻，突然撤去外力，系统将在光滑平面上沿x方向作微小振动［6］.

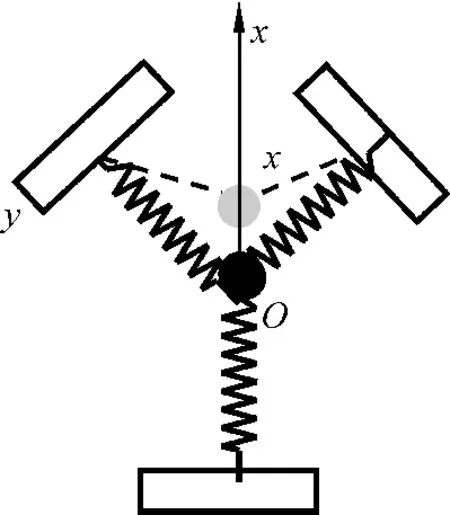
图3 二维对称3弹簧振子

系统的总势能为

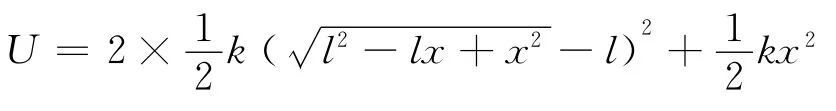
进行泰勒级数展开得

例4若在例3的基础上再加一个弹簧，4根劲度系数为k，原长为l的弹簧互成90°就得到如图4（a）所示的系统.平衡时各弹簧均恰好为原长，以平衡位置为坐标原点O，建立如图所示的坐标轴Ox.若在外力作用下将质点小球沿图4（a）的x方向移动微小距离，撤去外力，系统将在光滑平面上沿x方向作微小振动［6］.

系统的总势能为

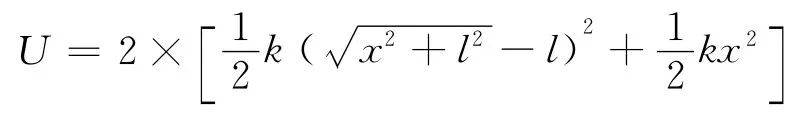
进行泰勒级数展开得

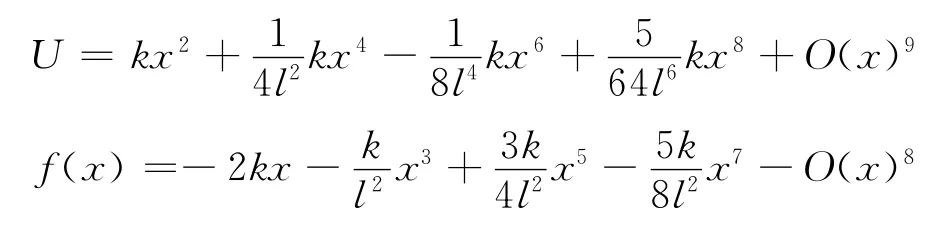
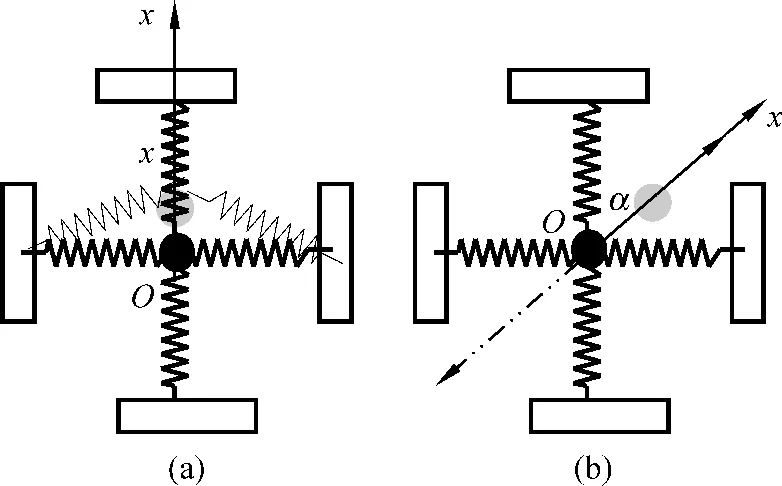
图4 弹簧振子系统

同样，若在外力作用下将质点小球沿图4（b）中所示的x方向移动微小距离，其中角α＝45°，可以得到系统的总势能为

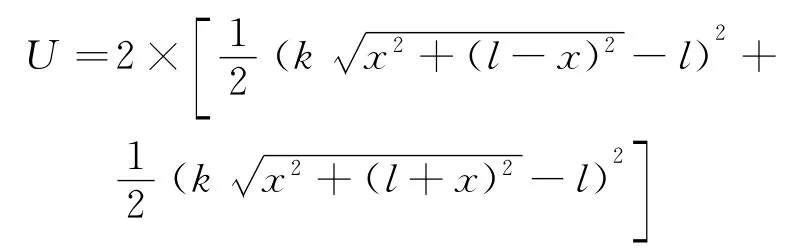
变形后进行泰勒级数展开得

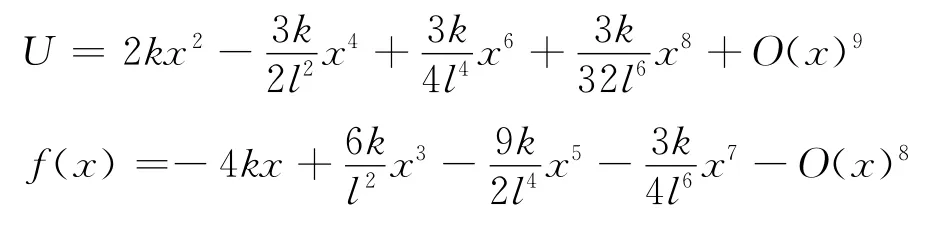
如果保留低阶无穷小，忽略高阶无穷小时，此系统的微小振动也是简谐振动.

3 结语

部分学生在学习弹簧参与的微小振动时，会产生这样的错误观念：①认为只要系统在平衡位置附近作往复的小振动就是简谐运动，但如例1所示，小球沿光滑的水平刚性细杆在平衡位置附近作往复振动，但系统不满足简谐运动的充要条件，其微小振动不是简谐运动；②认为多个弹簧参与的微小振动，如果其中每个弹簧产生的作用力为线性回复力，则系统在平衡位置附近的往复振动是简谐运动，但如例2所示，每个弹簧产生的作用力为线性回复力，但系统不满足简谐运动的充要条件，其微小振动不是简谐运动；③认为多个个弹簧参与的微小振动，不是简谐运动，但如例3和例4所示，分别有3个和4个弹簧参与的微小振动，但其系统满足简谐运动的充要条件，其微小振动是简谐运动.所以在判断弹簧参与的微小振动是否为简谐运动时，一定要根据简谐运动的充要条件进行详细分析.

［1］赵凯华，罗蔚茵.新概念物理教程力学［M］.北京：高等教育出版社，2005.

［2］漆安慎，杜婵英.力学［M］.北京：高等教育出版社，2003.

［3］梁绍荣，刘昌年，盛正华，等.普通物理学（第四分册）力学［M］.北京：高等教育出版社，2005.

［4］李栋.物体在稳定平衡位置附近的微小振动不一定都是简谐振动［J］.物理与工程，2006，16（1）：59-61.

［5］林少光，龚善初.弹簧振子非线性振动的周期计算［J］.湖南文理学院学报（自然科学版）.2009，21（4）：19-22.

［6］廖旭，任学藻.组合线性弹簧振子中的非线性振动［J］.大学物理，2008，27（2）：25-28.