修正Korteweg-de Vries方程的扭结-非线性波相互作用解

俞清云，程雪苹，2，李俊余，2，陈婷婷，井少杰，张景茹（.浙江海洋学院数理与信息学院，浙江舟山　36022；2.浙江省海洋大数据挖掘与应用重点实验室，浙江舟山　36022）

·研究简报·

修正Korteweg-de Vries方程的扭结-非线性波相互作用解

俞清云1，程雪苹1，2，李俊余1，2，陈婷婷1，井少杰1，张景茹1
（1.浙江海洋学院数理与信息学院，浙江舟山316022；2.浙江省海洋大数据挖掘与应用重点实验室，浙江舟山316022）

最近研究发现，对于任一Painlevé可积系统，截断Painlevé展开的留数正是原系统的非局域对称，亦称非局域留数对称。本文通过将修正Korteweg-de Vries（mKdV）方程的非局域留数对称局域化成延拓mKdV系统的李点对称，再利用李对称约化方法，得到mKdV方程的两类扭结和非线性波相互作用解。当移除非局域留数对称部分，该两类解退化为mKdV方程的一般对称约化解。

修正Korteweg-de Vries方程；非局域留数对称；对称约化；扭结-非线性波相互作用解

到目前为止，科学家们已经找到了很多研究非线性波的模型，如Korteweg de Vries（KdV）方程，修正Korteweg-de Vries（mKdV）方程，Kadomtsev-Petviashvili（KP）方程，非线性Schr？dinger（NLS）方程，sine-Gordon（SG）方程等等。这些系统几乎在所有物理领域都有广泛应用，尤其是在流体力学，等离子体物理，光学，凝聚态物理，量子物理和天体物理等领域［1-2］。同时，人们也利用各种有力手段找到了这些模型的许多不同类型的非线性波（非线性激发），如孤立子，扭结，椭圆周期波，Painlevé波等。在发现和构造出大量非线性激发模式后，随着研究的不断发展和深入，这些激发模式之间的相互作用也逐渐引起了人们的关注。到目前为止，孤立子-孤立子相互作用是众多相互作用激发模式中研究得最为广泛的。然而，尽管孤立子-孤立子相互作用已有大量研究，而要得到以上不同类型非线性波之间的相互作用却仍然是一个非常棘手的课题。最近我们关于这方面的研究有了新的进展［3-5］。

自LIE［6］第一次将李群理论应用到微分方程以来，李群方法已经成为数学和物理领域一个非常重要的课题。利用经典和非经典李群法［7-8］，可以降低偏微分方程（PDEs）的维度进而构建它们的解析解。与经典李群法类似，李点对称方法同样可以降低对应偏微分方程的维度。然而，运用对称理论解决非线性方程问题，特别是约化非线性偏微分方程，以往人们通常采用局域对称。倘若给定非线性偏微分方程的非局域对称，又如何达到降低维度的目的呢？一个简单且直接的方法就是将原方程进行延拓，使得原非线性系统的非局域对称变成延拓系统的局域对称。文献［4］中，作者通过将NLS系统的与达布变换相关的非局域对称延拓成李点对称，并运用对称约化方法得到了该方程的多种不同类型孤立子-非线性波的相互作用解。本文，我们将以mKdV方程为例，通过将其非局域留数对称局域化成对应延拓系统的李点对称，进而利用经典李对称法获得mKdV系统的扭结-非线性波相互作用解。

1　mKdV方程的非局域留数对称

考虑如下形式的mKdV方程

其中α，β为常数，分别描述非线性和色散效应。mKdV方程作为描述非谐晶格中声波的一个模型［9］，由MIURA［10］最早引入。该方程还可用于研究非线性光学中的波动问题［11］，尘埃等离子体中的尘埃声孤波［12］等。由于mKdV方程的广泛应用，对该方程的求解也成了研究该方程的一个重要组成部分。在过去的几十年里，人们利用多种研究手段得到了mKdV方程的各类数值或解析解［13-14］。

根据WTC（Weiss，Tabor，Carnevale）［15］方法，采用展开式

其中φ≡φ（x，t）是一个任意奇异流形。将展开式（1.2）代入mKdV方程（1.1）并由领头项分析（即平衡色散项uxxx和非线性项u2ux）得

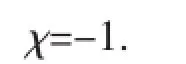
于是有mKdV方程的Painlevé截断展开式

将展开式（1.3）代入mKdV方程并消去φ的不同次幂得到如下五个方程

从以上最后一个方程（1.8）不难得到

其中δ=±1。比较方程（1.4）和（1.1）不难发现，u1正是满足mKdV方程的解，所以有mKdV方程的B？cklund变换

也就是说，如果u1是mKdV方程（1.1）的解，那么满足式子（1.10）的u也是该方程的解。从方程（1.5）不难验证，u0正是mKdV方程（1.4）的线性化方程（或对称方程），于是有u1的对称

从方程（1.7）并考虑（1.9）式可得到u1和流函数φ满足关系式

由于对称（1.11）包含流函数的一次导数而u1和流函数φ又有如上（1.12）式的关系，故（1.11）是u1的一个非局域对称，亦即非局域留数对称。继续考虑方程（1.6），得到（1.12）的相容性条件

也就是说，方程（1.12）和（1.13）的可积条件φxxt=φtxx正是mKdV方程（，1.4）。

对称（1.11）是非局域的，接下来我们将其局域化。若要局域化非局域对称（1.11），首先必须考虑取u的对称变换u→u+εσu的情况下，变量φ和

对应的变换是什么？也就是求方程（1.12）和（1.14）的线性化方程

需要指出的是，为方便起见，此处u和σu分别代替u1和σu1。如无特殊说明，以下段落均以此表示。将（1.11）代入方程组（1.15）并求解得

其中φ1满足相容性条件

该条件意味着等式φ1xt=φ1tx恒成立。

对称（1.11）和（1.16）表明原来｛x，t，u｝空间的非局域对称已成功局域化为延拓空间｛x，t，u,φ,φ1｝的李点对称。该对称的矢量形式可表示成或者也可以说，原空间的非局域对称只是延拓系统｛（1.1），（1.12），（1.14）｝的一个特殊的李点对称。

这里需要说明的是方程（1.13）和（1.17）可以包括到延拓系统中，或者也可以作为延拓系统的相容条件来处理。

2　mKdV方程的新对称约化

现在考虑延拓系统｛（1.1），（1.12），（1.14）｝的对称约化。根据经典李点对称方法，设对称的矢量形式满足

其中X，T，U，Φ，Φ1是关于变量｛x，t，u,φ,φ1｝的函数。对称（3.1）意味着该封闭系统在变换

意义下保持不变。由于系统不显含时间、空间变量，矢量形式的对称（2.1）可以写成函数形式

这里，σu，σφ，σφ1为对称方程，即延拓系统的线性化方程的解

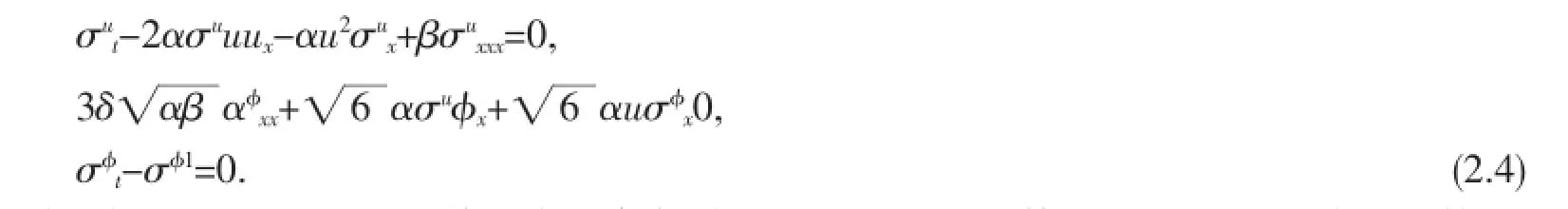
将对称（2.3）代入（2.4）并根据封闭延拓系统及其相容性条件消去ut，φx，φt，φ1x，φ1t等项，得到56个关于函数X, T,U,Φ,Φ1的决定方程。利用计算工具Maple解之得

其中c1，c2，c3，c4，x0，t0均为任意常数。于是对称（2.3）可以写成

设方程（3.6）中σu，σφ，σφ1为零，或等价于解特征方程

便得延拓系统的相似约化解。

接下来将分c1≠0和c1=0两种情形进行讨论。

2.1第一类相似约化（c1≠0）

令方程（2.6）中σu=σφ=σφ1=0，解得延拓系统的相似约化解

其中

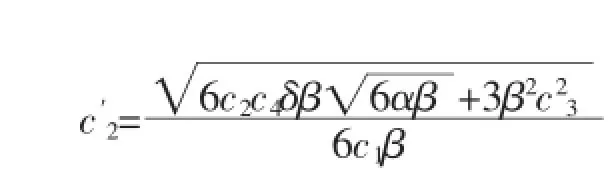
式（2.8）中U=U（ξ），Φ≡Φ（ξ），Φ1≡Φ1（ξ）为三个群不变函数，相似变量

将相似解（2.8）代入延拓系统｛（1.1），（1.12），（1.14）｝得约化方程

经过整理将约化方程（2.9）简化为

其中变换

且

一旦给定非线性偏微分方程（2.10）的解，那么结合（2.11），（2.12）和（2.8），可得延拓系统｛（1.1），（1.12），（1.14）｝的解。从解（2.8）不难分析，式中tanh部分的出现意味着此时群不变解是一个扭结和非线性波的相互作用。这里我们不再作深入讨论。

2.2第二类相似约化（c1=0）

当c1=0时，相似变量变为η=t-t0x，对应的相似解满足如下形式

再将解（2.13）代入延拓系统｛（1.1），（1.12），（1.14）｝，得到对应的约化方程

经过整理，方程（2.14）可进一步简化为

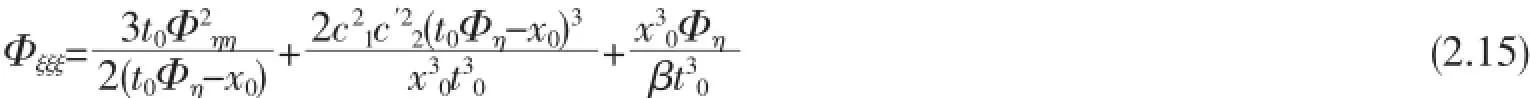
或

其中Ψ=t0Φη-x0。另外

从方程（2.16）知道，它的解可以由Jacobi椭圆函数给定。设方程（2.15）的解形如

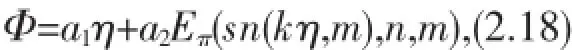
其中Eπ（，，）为第三类不完全椭圆积分，sn（，）≡sn为Jacobi椭圆正弦函数。将（2.18）代入（2.15）并消去sn的不同次幂，得到以下四种形式的解：

解1

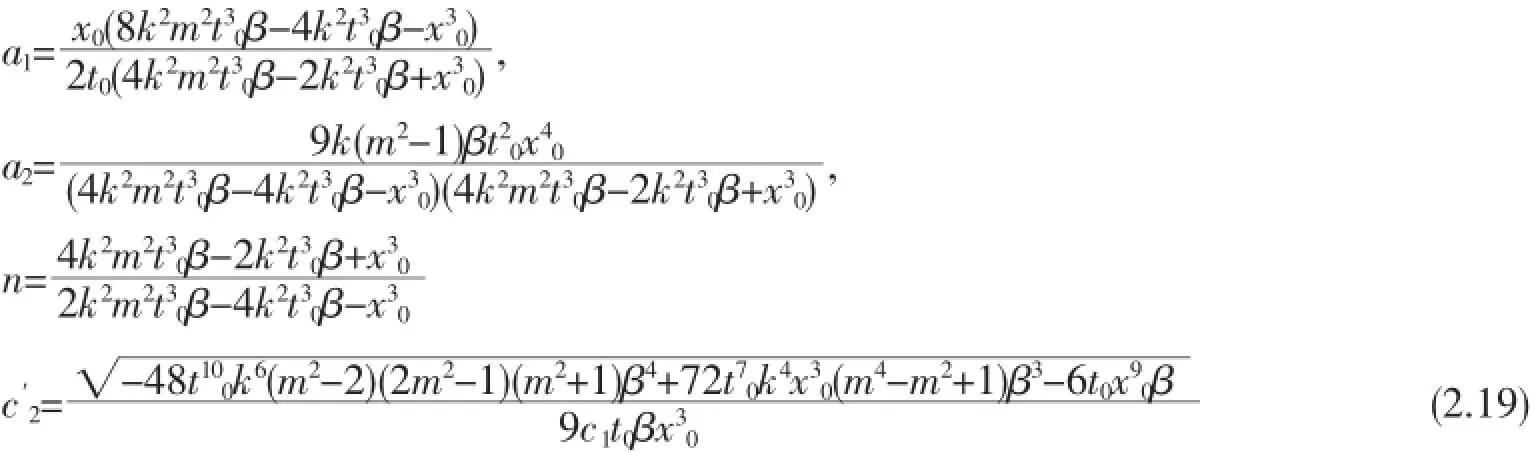
解2

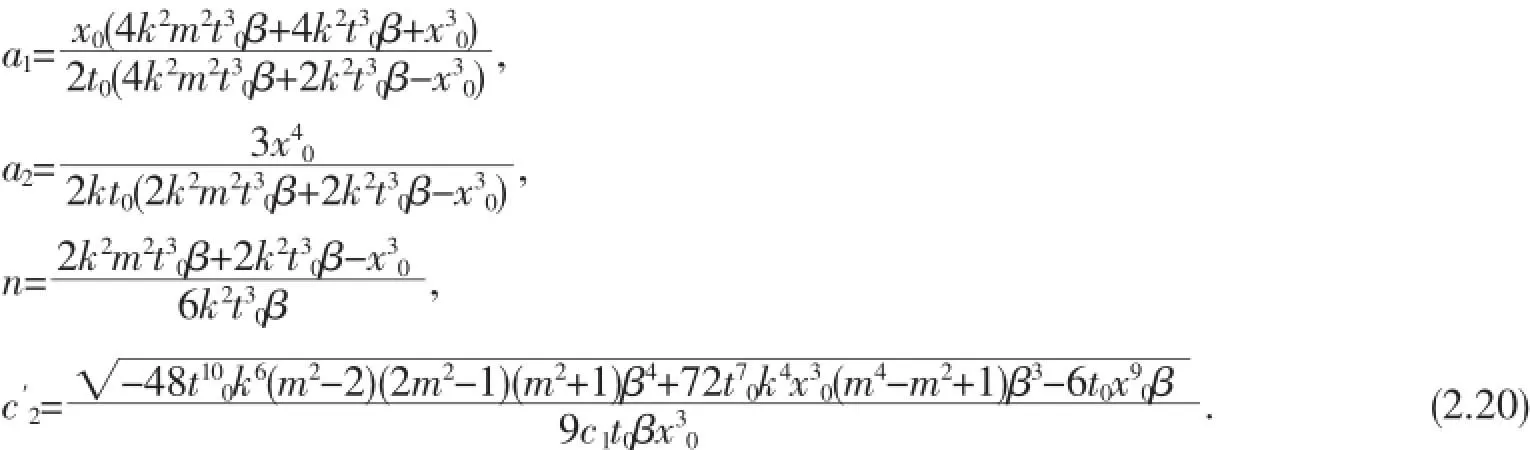
解3

解4其中另外六个常数ci（i=1，2，3，4），x0，t0，k仍为任意常数。

将满足（2.19）（或（2.20），或（2.21），或（2.22））的Φ，Φ1和U（由式（2.17）和（2.18）给定）代入（2.13）便得mKdV方程的相似解。由于式子过于冗长，此处不再详述。事实上，不论是约化解（2.8）还是（2.13），若从中移除周期波部分（即Φ部分），剩下的只是一个扭结，此即mKdV方程的一般对称约化解。

图1给出参数满足（2.21）式时mKdV方程的扭结-椭圆周期波相互作用解，其中1（a）为x=0处相互作用解随时间t的演化图，图1（b）为对应的三维演化图。解中其余参数设定为β=t0=k=1，m=0.99，α=6，x0=-2.5。图2展示了参数满足（2.22）时mKdV方程的扭结-椭圆周期波相互作用解，其中图2（a）为t=0时刻相互作用解随位置x的演化图，图2（b）为对应的三维演化图。解中其余参数设定为β=δ=k=1，m=0.99，x0=2.5，t0=-0.8，α=6。观察图1和2不难得到，扭结和椭圆波之间作用是伴有相移的弹性相互作用，其中相移为半波长。

3　结论

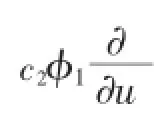
图1　mKdV方程的扭结-椭圆周期波相互作用解，其中参数满足（2.21）且取m=0.99，β=δ=t0=k=1，α=6，x0=-2.5. （a）x=0处相互作用解随时间演化图.（b）三维演化图.Fig.1 The kink-cnoidal wave interaction solution for the mKdV equation with the parameter satisfying（2.21）and m=0.99，β=δ=t0= k=1，α=6，x0=-2.5.（a）the time evolution of kink-cnoidal wave interaction solution at x=0.（b）the 3-D plot.

图2　mKdV方程的扭结-椭圆周期波相互作用解，其中参数满足（3.22）且取m=0.99，α=6，β=δ=k=1，t0=-0.8，x0=2.5.（a）t=0时刻相互作用解随演化图.（b）三维演化图.Fig.2　The kink-cnoidal wave interaction solution for the mKdV equation with the parameter selections（3.22）and m=0.99，α=6，β=δ=k=1，t0=-0.8，x0=2.5.（a）the kink dressed by a cnoidal periodic wave at t=0.（b）the 3-D plot.

值得强调的是，本文我们采用非局域留数对称及对称约化方法得到的相互作用解同样可以通过其他方法得到，包括与达布变换相关的非局域对称约化法［4］，相容Riccati展开法［16］，相容tanh函数展开法［17］等。当然，本文运用的方法和结果对其他众多非线性系统同样适用。至于在更多其他非线性系统中的应用、其他不同类型非线性波的相互作用解以及其他可能的新的物理应用等，我们将作后续研究和报道。

［1］KIVSHAR Y S，MALOMED B A.Dynamics of solitons in nearly integrable systems［J］.Rev Mod Phys，1989，61（4）：763-915.

［2］KIVSHAR Y S，LYTHER-DAVIES B.Dark optical solitons：physics and applications［J］.Phys Rep，1998，298（2/3）：81-197.

［3］LOU S Y，CHENG X P，TANG X Y.Dressed dark solitons of the defocusing nonlinear Schr？dinger equation［J］.Chin Phys Lett，2014，37（7）：070201.

［4］CHENG X P，LOU S Y，CHEN C L，et al.Interactions between solitons and other nonlinear Schr？dinger waves［J］.Phys Rev E，2014，89：043202.

［5］CHENG X P，CHEN C L，LOU S Y，Interactions among different types of nonlinear waves described by the Kadomtsev-Petviashvili equation［J］.Wave Motion，2014，51：1 298-1 308.

［6］LIE S.Vorlesungen über differentialgleichungen mit Bekannten infinitesimalen transformationen［M］//TEUBNER B G，1891.New York，1967.

［7］OLVER P J.Application of Lie groups to differential equation［M］.Springer，2000.

［8］BLUMAN G W，KUMEI S.Symmetries and differential equation［M］.Springer，1989.

［9］WADATI M.The modified Kortweg-de Vries equation［J］.J Phys Soc，Japan，1973，34：1 289-1 296.

［10］MIURA R M.Korteweg-de Vries equation and generalizations.I.A remarkable explicit nonlinear transformation［J］.J Math Phys，1968，9：1 202.

［11］AGRAWAL G P.Nonlinear fibre optics［M］.Academic press，2007.

［12］EI-SHAMY E F.Dust-ion-acoustic solitary waves in a hot magnetized dusty plasma with charge fluctuations［J］.Chaos，Solitons and Fractals，2005，25（3）：665-674.

［13］石玉仁，张娟，杨红娟，等.mKdV方程的双扭结单孤子及其稳定性研究［J］.物理学报，2010，59（11）：7 564-7 569.

［14］周杰，郝彦，王朝平.交通流优化速度差模型的非线性分析［J］.浙江海洋学院学报：自然科学版，2012，31（6）：563-566.

［15］WEISS J，TABOR M，CARNEVALE G.The Painlevé property for partial differential equations［J］.J Math Phys，1983，24：522.

［16］LOU S Y.Consistent Riccati expansion and solvability［EB/OL］.2013，arXiv：1308.5891.

［17］CHEN C L，LOU S Y.CTE solvability and exact solution to the Broer-Kaup system［J］.Chin Phys Lett，2013，30：110202.

Interactions between Kinks Described by Modified Korteweg-de Vries Equation and Nonlinear Waves

YU Qing-yun1，CHENG Xue-ping1，2，LI Jun-yu1，2，et al
（1.School of Mathematics，Physics and Information Science，Zhejiang Ocean University，Zhoushan316022；
2.Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province，Zhoushan 316022，China）

Recently，it was found that the symmetry related to the Painlevé truncated expansion is just the residue with respect to the singular manifold，which is called non-local residual symmetry.In this paper，by localizing the nonlocal residual symmetry of modified Korteweg-de Vries（mKdV）equation，which is related to the truncated Painlevé expansion，to the Lie point symmetry of extended modified Korteweg-de Vries system，two types of exact solutions of mKdV equation have been obtained by using the symmetry reduction method.These two types of solutions reduce to the usual similarity reduction solutions of mKdV equation when the nonlocal symmetry is removed.

modified Korteweg-de Vries equation；nonlocal residual symmetry；symmetry reduction；kink-nonlinear wave interaction solution

O175.29

A

1008-830X（2015）04-0387-08

2015-01-10

浙江省大学生科技创新活动计划（新苗人才计划）项目（2014R411016）；国家自然科学基金（11505154）

俞清云（1992-），男，浙江慈溪人，研究方向：凝聚态物理.

程雪苹（1982-），女，浙江温岭人，副教授，研究方向：数学物理.E-mail：chengxp2005@126.com