螺旋桨轴承力计算方法的对比分析

朱　鹏，毕　毅，叶金铭

螺旋桨轴承力计算方法的对比分析

朱鹏，毕毅，叶金铭

海军工程大学舰船工程系，湖北武汉430033

为了对螺旋桨的轴承力进行研究，在标模SUBOFF尾部同一位置装上4种不同的螺旋桨，分别用CFD方法、拟定常方法以及升力线理论进行螺旋桨轴承力理论预报。根据计算结果，分析侧斜、叶数对螺旋桨轴承力的影响以及不同方向轴承力的相对大小，并对3种方法的优缺点进行总结。结果表明：CFD与升力线理论方法更适合工程需要，尤其是对侧斜较大的桨叶，其较拟定常方法有着比较好的预报效果；同时，升力线理论方法在计算效率方面优于CFD方法；并且螺旋桨轴承力随着叶数的增多、侧斜度的增大而减小；轴承力在y方向上力的分量均大于x方向。

螺旋桨；轴承力；CFD；拟定常方法；升力线理论

期刊网址：www.ship-research.com

引用格式：朱鹏，毕毅，叶金铭.螺旋桨轴承力计算方法的对比分析［J］.中国舰船研究，2015，10（1）：83-87.

ZHU Peng，BI Yi，YE Jinming.Comparison analysis of three kinds of computational methods for the bearing force of

propellers［J］.Chinese Journal of Ship Research，2015，10（1）：83-87.

0　引言

由于船（艇）体伴流场的不均匀而产生的不定常力作用在桨叶上，然后通过轴承传递到船体的这一类激振力称为轴承力。潜艇螺旋桨轴承力容易引起艇体尾部结构产生振动，由此引发的艇体尾部结构振动噪声是潜艇的重要噪声源，会对潜艇的隐蔽性带来重大影响，所以螺旋桨轴承力，特别是潜艇螺旋桨轴承力一直是造船界研究的重要问题。

目前对于螺旋桨轴承力的计算，国内外学者做了大量研究，除了比较常规的拟定常方法外［1］，Kerwin等［2］利用涡格升力面法计算了螺旋桨非定常工作。叶金铭和谭廷寿等［3-4］应用面元法预报了螺旋桨轴承力。随着CFD方法的快速发展，CFD方法已被广泛应用于船舶各种水动力问题的计算与分析［5-7］，张志荣和洪方文［8］应用准定常、滑移网格和运动网格考察分析了大侧斜螺旋桨在斜流下的非定常性能，计算显示，滑移网格和运动网格能够较好地模拟螺旋桨斜流下的非定常性能，精度也要好于准定常方法。本文的研究基于在螺旋桨设计之初需要对大量螺旋桨的各种参数，如侧斜分布进行优化设计的目的，为了提高设计工作效率，需要在能够较快得到计算结果的同时又能保证一定的计算精度。为此，本文将基于工程实际的需要，在用拟定常方法、CFD方法计算螺旋桨轴承力的基础上，建立一种用升力线理论计算螺旋桨轴承力的方法。采用3种方法对多只螺旋桨的轴承力进行计算，然后根据计算结果分析螺旋桨侧斜、叶数等参数对轴承力的影响，总结各种计算方法的优缺点。

1　原理概论

1.1RANS方程

对于三维不可压缩的粘性流体，无量纲化的RANS方程在笛卡尔坐标系下的张量形式为：

连续性方程

动量方程为：

式中：i，j=1，2，3；ρ为流体密度；υ为流体的运动粘性系数；Fi为外力项；ui为平均速度；p为平均压力；u′i为速度脉动量。

1.2螺旋桨拟定常方法

本方法的基本假设是忽略周向伴流，推力和转矩集中作用在某一半径处。其推力公式为

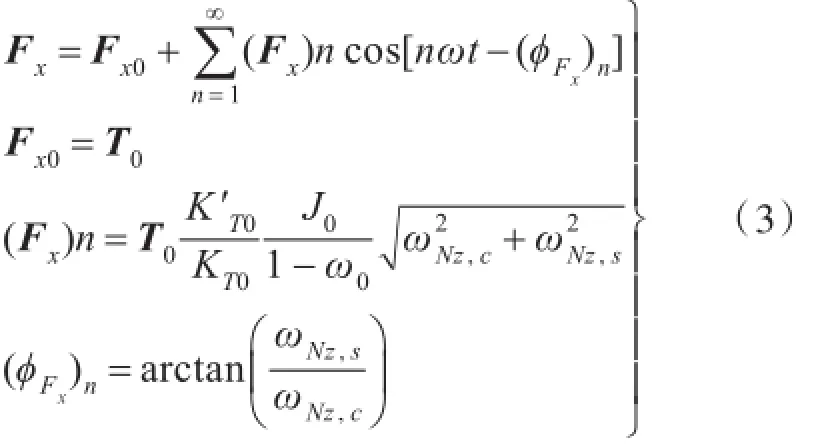
式中：ω=2πnZ，为对应于叶频的元周波数；T0=）?，其余各方向的力与力矩参见文献［1］，在此不再赘述。

1.3螺旋桨升力线理论计算方法

拟定常方法无法考虑螺旋桨侧斜分布［2］、负荷纵向分布对轴承力的影响，而这些因素对螺旋桨轴承力的影响又十分明显，所以在计算侧斜螺旋桨轴承力时，采用拟定常方法往往会出现较大误差，需要对该方法进行修正。本节采用升力线理论对螺旋桨的轴承力进行计算，计算方法如下。在径向上分为L段，不计粘性影响，主叶位于θ角位置时，第j段产生的推力、轴向转矩和切向力可以分别采用下式计算：

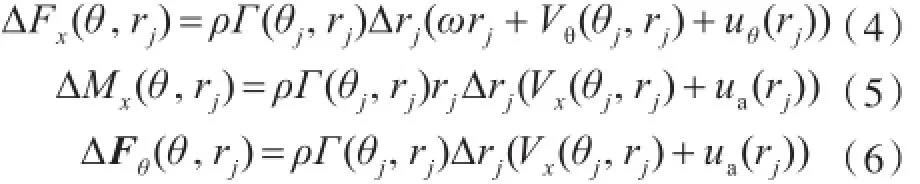
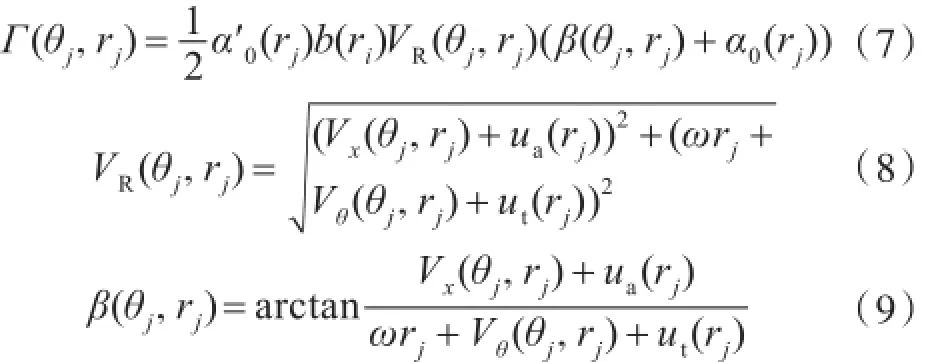
式中：α′0（rj）为升力系数的导数；α0（rj）为零升力攻角；β（θj，rj）为水动力螺距角；ut为切向诱导速度；VR为剖面来流速度；b为弦长。

ua（rj）和ut（rj）可以用升力线理论计算得到。螺旋桨主叶各段处的推力、转矩和切向力可写成如下形式：

式中，Z为桨叶叶数。螺旋桨其他方向上的力和转矩可以通过推力和切向力计算得到，由于篇幅限制，在此不再赘述。

2　计算与分析

2.1计算对象

计算对象为SUBOFF潜艇模型，模型艇长17.46 m。分别将4种不同的桨叶安装在距艇首16.92 m处，4种不同桨叶分别为DTMB 4381，DTMB 4382，DTMB 4383以及HG7-36。其中，DTMB 4381，DTMB 4382和DTMB 4383桨为五叶桨，侧斜分别为0°，36°，72°。HG7-36为七叶桨，侧斜36°。它们的直径均为920 mm，如图1所示。该模型坐标系规定如下：x轴沿着艇艏指向艉部，z轴垂直于艇体并由水下指向水面，y轴服从右手定则，如图2所示。

图1　不同桨叶正视图Fig.1　Elevation view of different blades

图2　SUBOFF计算模型Fig.2　The computing model of SUBOFF

2.2湍流模型的选取

用拟定常方法和升力线理论计算轴承力时，需要先用CFD方法计算得到SUBOFF全附体模型桨盘面处的伴流场，因此，本文首先讨论不同湍流模型对伴流计算结果的影响［9］。选取常用的SST k-ω、标准k-ε和RNG k-ε这3种模型。将流场的轴向速度无因次化后与已知实验数据进行对比（桨盘面位于x/L=0.978处，雷诺数Re=1.2×107），其结果如图3所示。由图可发现，SST k-ω模型在流场方面能够较为准确地反应流场分布特点，故在下文中均以该模型进行数值运算。

2.3计算条件设置

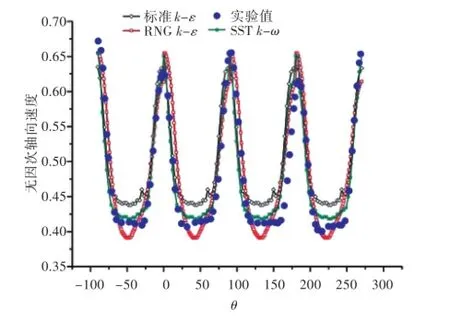
图3　r/R=0.25处无因次轴向速度分布计算结果与实验值的比较（Re=1.2×107）Fig.3　Comparison of non-dimensional axial velocity distribution calculation results and the experimental values at r/R=0.25（Re=1.2×107）

1）计算域长度：艇体外域入口距艇艏部约1.5倍艇长，出口距艇体艉部约为4倍艇长，上、下高度距艇体约1.5倍艇长。

2）入口与出口设置：入口设置为速度入口，速度为2.572 m/s，出口设置为压力出口。

3）旋转域设置：定常计算时，旋转域采用MRF模型，转速n=180 r/min。

2.4轴承力计算结果与分析

通过CFD方法计算得到艇体尾部伴流场后，就可以用拟定常方法和升力线理论对螺旋桨轴承力进行计算。用拟定常方法计算螺旋桨轴承力时，先对桨盘面处的伴流场进行傅立叶分析，得到各半径位置处各阶伴流分数幅值（表1），进而可得到不同方向轴承力的一阶叶频幅值（表2、表3）。

表1　SUBOFF艇体在伴流的谐调成分Tab.1SUBOFF hull in the coordination component of wake

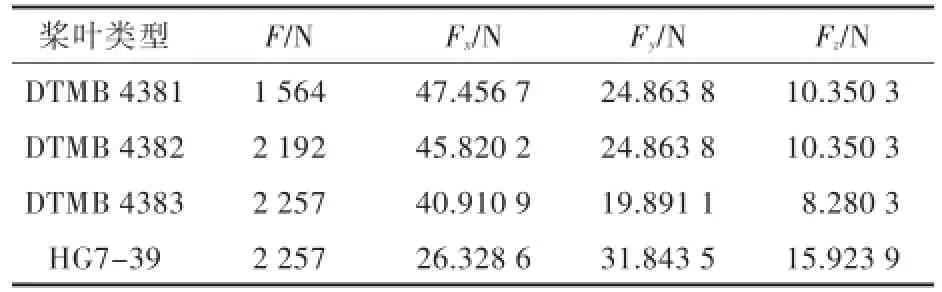
表2　拟定常方法计算的螺旋桨力的一阶叶频幅值Tab.2First order blade frequency amplitude of propeller force of quasi steady method

表3　拟定常方法计算的螺旋桨扭矩的一阶叶频幅值Tab.3First order blade frequency amplitude of propeller torque calculation of quasi steady method

采用CFD方法计算艇后螺旋桨轴承力时，螺旋桨附近区域用非结构化网格，其他区域用结构化网格，如图4所示。先运用定常法运算至收敛，待收敛后，再采用滑移网格模拟螺旋桨转动情况，并实时记录螺旋桨在空间坐标系上的推力以及扭矩的时域信号（计算时间长度采取4个螺旋桨旋转周期以上）。

图4　加桨后（DTMB 4382桨）SUBOFF尾部网格Fig.4　The tail grid of SUBOFF with DTMB 4382 propeller

将CFD方法和升力线理论的时域计算结果进行傅立叶分析，可以得到不同方向轴承力的一阶叶频幅值。将采用3种方法得到的轴承力一阶幅值进行无因次化，方法如下：

-F，-M分别为螺旋桨推力与扭矩的平均值。3种方法的计算结果如图5所示（图中，1代表DTMB 4381桨，2代表DTMB 4382桨，3代表DTMB 4383桨，4代表HG7-36桨）。由图可以看出，计算DTMB 4381这种0°侧斜桨时，CFD计算值与升力线理论值和拟定常方法计算值均很接近，说明采用该3种方法均能预报0°侧斜的螺旋桨幅频值。

由图5还可以看出，从CFD方法和升力线理论的计算结果来看，DTMB 4381，DTMB 4382和DTMB 4383这3只螺旋桨的轴承力随着侧斜的增大而减小，这说明增加侧斜能有效降低螺旋桨轴承力，CFD方法和升力线理论能够反映出侧斜对螺旋桨轴承力的影响。对于DTMB 4381桨、DTMB 4382桨、DTMB 4383桨，采用拟定常经验公式轴承力变化不大，基本相当，分析其原因，主要是因为拟定常公式未考虑侧斜的影响。故当侧斜较大时，采用拟定常方法会产生较大误差，无法满足工程应用需要。

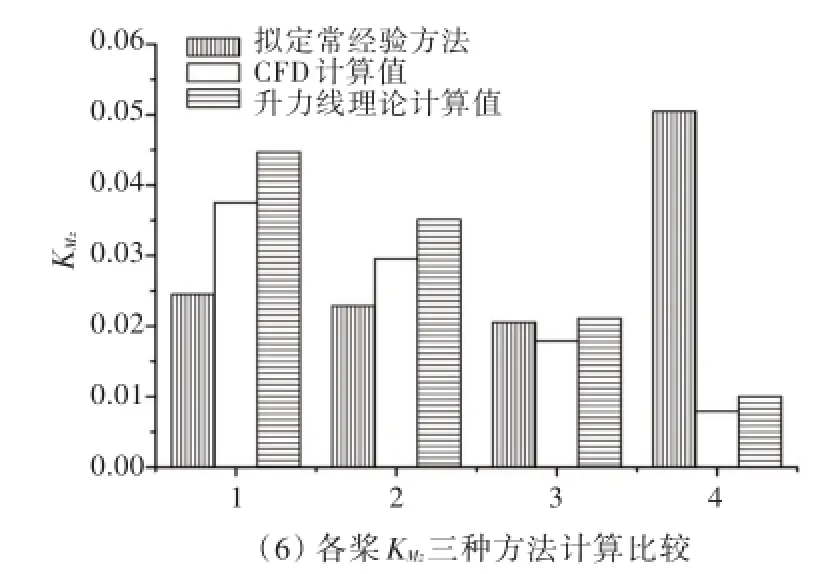
图5　不同桨叶在不同方向上力KF与KM比较Fig.5　KFand KMin the different directions for different blades

从图1可以看出，DTMB 4382桨与HG7-36桨有着相同的侧斜角度和不同的叶数。再从图5中此2个桨的比较来看，在侧斜角度不变的情况下，螺旋桨叶数由5叶增加到7叶时也能降低轴承力。如图6所示，在DTMB 4381，DTMB 4382，DTMB 4383和HG7-36桨中，轴承力在y方向上的力均大于x方向。

因此，对于DTMB 4382，DTMB 4383和HG7-36桨升力线理论方法和拟定常方法相比，其计算值更接近CFD值，故用升力线方法在计算螺旋桨轴承力，特别是大侧斜螺旋桨轴承力时比拟定常方法的精度高。通过该方法可以较快、较准确地计算螺旋桨的轴承力，特别是在螺旋桨设计时，可以根据伴流分布的特点快速筛选出侧斜分布形式。

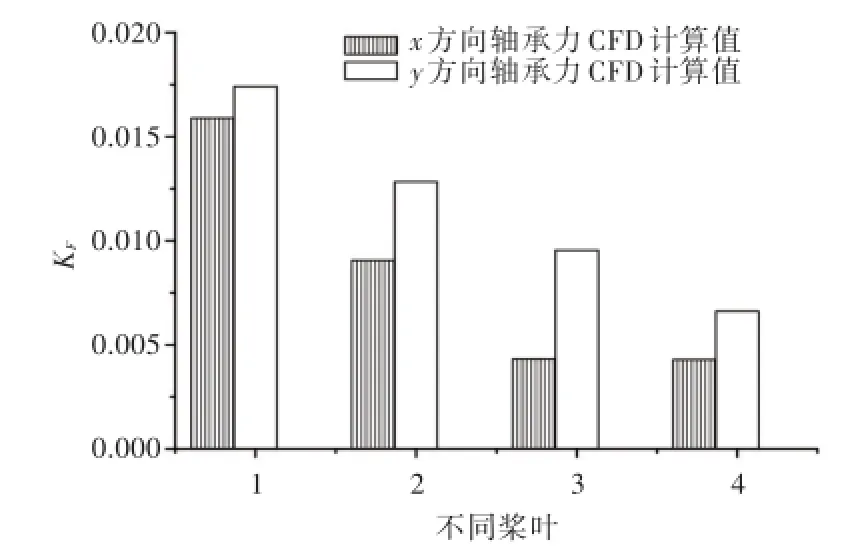
图6　同一桨叶在不同方向KF比较Fig.6　KFin different directions for the same blade

3　结语

通过对以上计算结果的比较分析可知，对于螺旋桨轴承力的计算，CFD有着较好的精度，但需要耗费大量时间。在工程实际运用中，往往需要对不同侧斜分布形式的多种方案进行综合比较，拟定常公式又无法正确反映侧斜对螺旋桨轴承力的影响。基于此，本文提出用升力线理论方法来计算螺旋桨轴承力，它既能实现快速筛选，又能保证一定的精度，大大提高了效率，保证了工程进度。

［1］盛振邦，刘应中.船舶原理（下册）［M］.上海：上海交通大学出版社，2003.

［2］KERWIN J E，LEE C S.Prediction of steady and un⁃steady marine propeller performance by numerical lift⁃ing-surface theory［J］.Society of Naval Architects and Marine Engineers，1978：218-253.

［3］叶金铭，熊鹰.螺旋桨轴承力预报方法分析［J］.船舶工程，2003，25（3）：16-18. YE Jinming，XIONG Ying.Analysis of prediction meth⁃od of forces exerted on propeller bearing［J］.Ship Engi⁃neering，2003，25（3）：16-18.

［4］谭廷寿，贺伟.螺旋桨非定常轴承力计算［J］.船海工程，2006（2）：42-46. TAN Tingshou，HE Wei.Calculation of unsteady shaft forces of propeller［J］.Ship and Ocean Engineering，2006（2）：42-46.

［5］The Specialist Committee on Computional Fluid Dy⁃namics［C］//26th International Towing Tank Confer⁃ence.Rio de Janeiro，Brazil，2011.

［6］黄胜，王超.不同湍流模型在螺旋桨水动力性能计算中的应用与比较［J］.哈尔滨工程大学学报2009，30（5）：481-485. HUANG Sheng，WANG Chao.Application and compar⁃ison of different turbulence models in the computation of a propeller's hydrodynamic performance［J］.Journal of Harbin Engineering University，2009，30（5）：481-485.

［7］王福军.计算流体动力学分析——CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［8］张志荣，洪方文.斜流中螺旋桨性能数值分析方法研究［C］//船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议.银川，2007.

［9］刘志华，熊鹰，叶金铭，等.基于多块混合网格的RANS方法预报螺旋桨敞水性能的研究［J］.水动力学研究与进展（A辑），2007，22（4）：450-456. LIU Zhihua，XIONG Ying，YE Jingming，et al.Study on the prediction of propeller open-water performance using RANS formula and multi-block hybrid meshes［J］.Journal of Hydrodynamics（Ser.A），2007，22（4）：450-456.

［责任编辑：田甜］

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1201.009.html

Comparison Analysis of Three Kinds of Computational Methods for the Bearing Force of Propellers

ZHU Peng，BI Yi，YE Jinming
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

In order to study the bearing force of propellers，four different blades are fitted onto the same place at the end of a standard mold of SUBOFF.With the help of CFD，quasi steady empirical formula，and the lifting line theory method，the bearing force can be predicted.Based on the calculation results，this pa⁃per analyzes the effects of the blade number of propeller on the bearing force as well as the relative strength of the force in various directions.Finally，the advantages of all three kinds of methods are summarized，and it is observed that the lifting line theory method and the CFD are more suitable than quasi steady method for engineering applications，especially for the highly skewed blade.Meanwhile，the lifting line theory method has a higher computational efficiency than that of CFD method.In addition，the propeller bearing force decreases as the number of blades increases or the skewness increases，and the overall weight bear⁃ing force in the y direction is greater than that in the x direction.

propeller；bearing force；CFD；quasi steady empirical formula；lifting line theory

U664.33

A

10.3969/j.issn.1673-3185.2015.01.012

2014-07-02

网络出版时间：2015-1-28 12:01

国家自然科学基金资助项目（51009145）

朱鹏，男，1991年生，硕士生。研究方向：舰船流体力学。E⁃mail：303853977@qq.com

毕毅，男，1963年生，副教授。研究方向：舰船操纵性

叶金铭（通信作者），男，1978年生，博士，副教授。研究方向：舰船螺旋桨性能