波浪中船舶操纵性数值预报及自航模验证

朱冬健，马　宁，2，顾解忡，2，邓德衡，2

波浪中船舶操纵性数值预报及自航模验证

朱冬健1，马宁1，2，顾解忡1，2，邓德衡1，2

1上海交通大学船舶海洋与建筑工程学院，上海200240
2海洋工程国家重点实验室，上海200240

基于统一理论，考虑横荡、纵荡、艏摇平面三自由度操纵和横摇耦合，建立四自由度模型，按照MMG模型将船体上的力分为船体力、螺旋桨力和舵力，采用耦合模型叠加波浪力的方式来预报船舶在波浪中的操纵性。波浪力采用三维面元法计算，并根据船舶实时速度和遭遇浪向进行二维插值。通过对比仿真数据与自航模试验数据，验证了模型的准确性。预报了在不同波浪工况下的船舶操纵性，验证了二阶力是船舶回转漂移的主要原因。比较了不同波高对船舶在波浪中操纵性的差异，研究结果表明：波高越大，船舶回转的纵向和横向漂移越明显，并且Z形试验中的第1超越角和达到时间越长。

操纵性；自航模试验；MMG模型；统一理论；时域模拟

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1201.010.html

期刊网址：www.ship-research.com

引用格式：朱冬健，马宁，顾解忡，等.波浪中船舶操纵性数值预报及自航模验证［J］.中国舰船研究，2015，10（1）：76-82，96. ZHU Dongjian，MA Ning，GU Xiechong，et al.Numerical prediction and free-running model validation of ship maneu⁃vering in waves［J］.Chinese Journal of Ship Research，2015，10（1）：76-82，96.

0　引言

船舶运动数学模型的建立是为了对包括操纵在内的船舶运动进行仿真。1948年，Davidson［1］研究了船舶在波浪中的操纵性，首次提出波浪中操纵方程，之后运动模型和操纵仿真都取得了很大的发展。1976年，日本操纵性数学模型小组（MMG）用几年时间开发了分离式的水动力模型，进行了一系列的约束模试验，对船体、螺旋桨、舵的水动力以及相互干扰进行了系统的研究。

波浪中船舶操纵性较为经典的理论模型分别由Kijima和Hamamoto等［2-3］提出。Kijima建立了四自由度运动模型，模型考虑了横摇对于水动力导数的影响，同时考虑了一阶和二阶波浪力，适于计算波浪中的回转运动及Z型操纵运动等问题。Hamamoto全面计算了6个自由度的运动，考虑各个运动间惯性力耦合，能够模拟船舶在波浪中的骑浪、横甩、倾覆等现象，但忽略了二阶波浪力以及波浪对水动力导数的影响。Yasukawa［4］使用S175集装箱船在规则波和不规则波中进行自航模试验和基于MMG模型的仿真回转试验，并将二者做了对比。Ayaz等［5］利用六自由度模型对于尾追浪中的船舶操纵性做了细致的研究，对于横甩、骑浪等特殊操纵运动均做出了预报，并通过试验予以验证。1990年Nonaka［6］采用双时标展开法，证明在理想流体中，船舶在波浪中的运动可以看成低频运动和高频运动的叠加。所以将船舶在波浪中的运动看成波浪漂移力作用下的操纵运动和波浪扰动力作用下的摇荡运动的叠加。近年来也发展出了将操纵和耐波相结合的统一理论，如Skejic等［7］考虑了操纵性和耐波性的耦合问题，在2个不同时间尺度下分别研究船舶在波浪中的操纵和耐波运动，建立了操纵耐波统一理论，一阶波浪力采用STF切片法计算，二阶漂移力采用3种不同的方法并做了相应的对比。

本文根据Skejic和Faltinsen提出的统一理论建立操纵性和横摇四自由度耦合模型，按照MMG分离式模型将作用在船体上的力分为船体力、桨力和舵力，对静水和迎浪规则波中一艘S175集装箱船进行数值仿真与试验验证。波浪力借助软件HydroStar采用三维面元法计算，并根据船舶实时速度和遭遇浪向进行二维插值获取。验证模型准确性后分析船舶在相同波频，不同波高的工况下操纵性能的差异。

1　坐标系与数学模型

1.1操纵性模型

研究船舶在海上的运动时，通常采用地球坐标系和船体坐标系，2坐标系在与海平面齐平的同一水平面内［8］。船舶在各坐标系下运动的速度、角速度及正方向如图1所示。

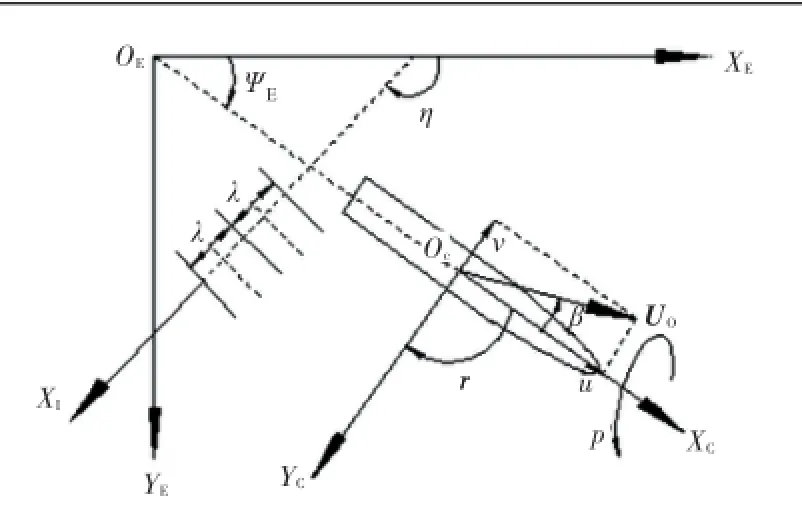
图1　定义船舶运动坐标系Fig.1　Definition of ship motions and coordinate systems

统一模型中，操纵性运动根据MMG模型，将作用在船上的力分离成船体力、螺旋桨力、舵力和波浪干扰力。考虑横荡、纵荡、艏摇和横摇4个自由度耦合，数学模型如式（1）所示：

式中：m和Ixx，Izz为船舶的质量和惯性矩；mx，my和Jxx，Jzz为附加质量和附加惯性矩；zG为相对于船体坐标系下的重心垂向坐标；分别为船体力、舵力、阻力、螺旋桨力和波浪力；u，v为船舶纵荡、横荡速度；r，p为艏摇和横摇角速度。

求得船体坐标系下的速度和角速度后，需要转换到地球坐标系下进行物理量积分，才能得到船舶的实时位置和速度。下面介绍坐标系的转换方法。

式中：x，y，ψ，ϕ分别为船体坐标系下的位置坐标；XE，YE，ΨE，ΦE分别为地球坐标系下的位置坐标。地球坐标系下的物理量可以通过欧拉角转换矩阵E4×4得到：

式中，

1.2船体力

作用在船体上的流体力可以分为惯性力和粘性力，惯性力是指船舶在理想流体中做非定常运动时所受的水动力，以附加质量和附加惯性矩的形式表现，粘性力部分可以展开为水动力导数的形式：

将无因次力乘以相应系数便可得到实际船体力，无因次水动力系数可由理论计算、经验公式或PMM试验确定。本文采用文献［4］的数据。船体横摇力矩KH可表示为：

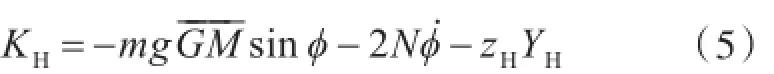
1.3螺旋桨力

船舶前进时静水中阻力R与其纵向速度u有关：

式中：ρ为流体密度；d为吃水；X′uu为无因次化的阻力系数。

螺旋桨产生的纵向推力以平衡阻力，推力XP可表示为：

式中：t为推力减额，由汉克歇尔公式［9］确定，t=0.5CP-0.12；nP，DP为螺旋桨的转速和直径，转速由测速试验获得；推力系数KT（JP）= J0+J1JP+J2J2P，敞水系数J0，J1，J2由敞水试验获得，JP为进速系数：

式中：wP为有效伴流系数，由直航时桨处伴流系数wP0和漂角βP修正［10］得到：wP=wP0·exp（-4β2P）。

1.4舵力

操舵时作用在舵上的流体力可表示为：

式中：δ为操舵角；tR为舵阻力减额系数，通常tR=0.29；aH为操舵诱导船体横向力的修正因子，aH与船的方形系数Cb有关［10］，aH=0.678 4-1.337 4Cb+1.889 1C2b；xH为操舵诱导船体横向力作用中心至船体重心的距离，它们是船体与舵的相互干扰，xH=-L（0.4+0.1Cb）；FN为舵的正压力：

式中：AR为舵面积；fα为舵升力系数，由藤井公式［10］确定，，λR为舵的展弦比；UR为舵的来流速度为舵来流的有效冲角，分别为舵来流的速度分量：

式中：ε，κ为试验修正系数；γR为整流系数，采用文献［4］数据；为舵处漂角，，无因次化的修正系数几乎不随船型变化，一般取l′

R≈-0.9～-1.0［10］；δ0为零正压力舵角，对矩形舵，可采用藤井公式确定：δ0=-2×（1-u（1-wP）/（nPP））［10］，P为螺旋桨的螺距，此公式得到的舵角需要进行弧度转换。

1.5波浪力

考虑到一阶力主要引发船体摇荡运动，二阶力主要改变船舶航向和航迹。本文考虑航速对船舶所受波浪力的影响，根据无限水深线性势流理论，采用基于三维面元法的商用软件HydroSTAR计算船体不同航速（傅汝德数Fn=0～0.15，ΔFn=0.015）、波频（波长船长比λ/L=0.5，0.7，1，1.2，1.4）、遭遇浪向（χ=0°～360°，Δχ=10°）下频域一阶扰动力和二阶漂移力，通过频、时域转换后计入时域操纵方程。方程中横荡、纵荡、艏摇方程只考虑二阶力影响，横摇方程考虑一阶干扰力。最后将波浪力按照实际遭遇浪向角和航速进行二维插值。图2为对象船模的gambit模型。

图2S175 gambit模型Fig.2　S175 gambit model

图3为规则波波浪工况下（ω=5.39 rad/s，HW=1 m），船模在不同航速和遭遇浪向下所受x，y方向二阶力DFX，DFY和二阶转艏力矩DMZ。

图3　二阶力与力矩三维图示Fig.3　Three-dimensional graph of second-order force（moment）

2　自航模试验

本文研究对象为上海交通大学一条S175自航船模（图4），船模尺度比为57.686，其主尺度及桨舵数据如表1所示。

图4　船模试验及桨和舵Fig.4　Model test，propeller and rudder

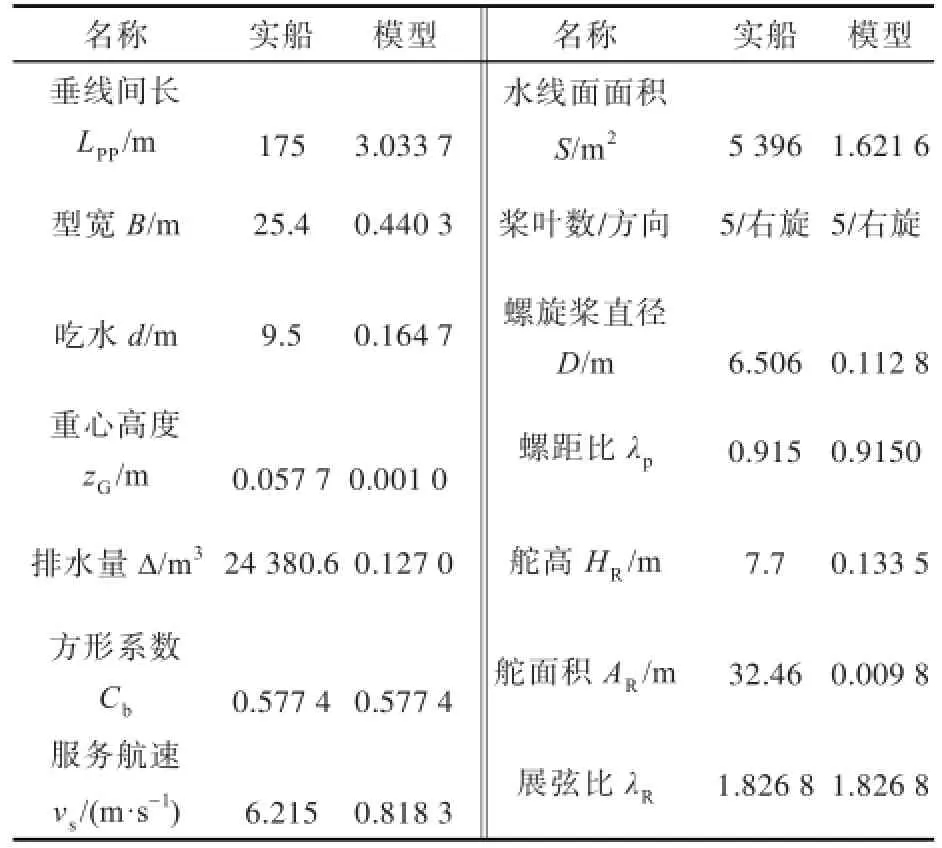
表1　船模主尺度及桨舵数据Tab.1Main dimensions of ship model and data of propeller and rudder

此次试验分为如下几类：

1）倾斜试验。通过移动货物，测量货物在不同位置时船舶横摇角的变化，确定船舶在静水中的初稳性高

式中：m0为试验时记录的货物重量；l为移动距离；ϕ0为变化的横摇角。

2）自由横摇衰减试验。通过测量船舶在初始倾角的自由横摇时历来确定船舶横摇固有周期Tϕ、附加惯性矩和阻尼。其中：Tϕ=2.3 s；总横摇惯性矩；阻尼

图5　横摇衰减曲线Fig.5　Curve of roll extinction

3）螺旋桨敞水试验。通过测量得到桨的推力系数与进速系数的特征曲线，通过拟合曲线可得系数J0=0.494 6，J1=-0.410 4，J2=-0.078 6（图6）。

图6　螺旋桨特征曲线Fig.6　Characteristic curve of propeller

4）测速试验。通过速度测量得到船舶达到服务航速（傅汝德数Fn=0.15）时螺旋桨的转速nP=594 r/min。

5）船舶操纵性试验。该试验分为静水和波浪中的回转试验以及Z形试验，部分波浪工况如表2所示。

表2　波浪工况Tab.2Wave cases

3　数值计算与试验验证

3.1回转仿真与验证

为了验证总横摇惯性矩和横摇阻尼的准确性，保证耦合模型中横摇模块的有效性，本文通过仿真船模在静水中的自由横摇衰减，并与模型试验进行对比。计算结果表明自由横摇试验在幅值衰减和横摇周期都具有较好的一致性（图7）。图中，Cal.表示仿真计算结果，Exp.表示试验结果。

图7　自由横摇衰减曲线Fig.7　Curve of free roll extinction

在不考虑波浪干扰的情况下，应用提出的数学模型对船模进行静水回转运动的仿真，仿真条件为左右舵35°，操舵速度13（°）/s。并与自航模试验结果进行对比。

图8和图9为静水无因次回转轨迹以及对应的艏向角时历。左舵回转的艏向角试验结果的波动是测量信号受干扰造成的。左右回转并不对称是由于船模使用的是单桨右旋螺旋桨，操左舵和右舵时在流场中的伴流不同。对比结果表明仿真结果与试验吻合较好。

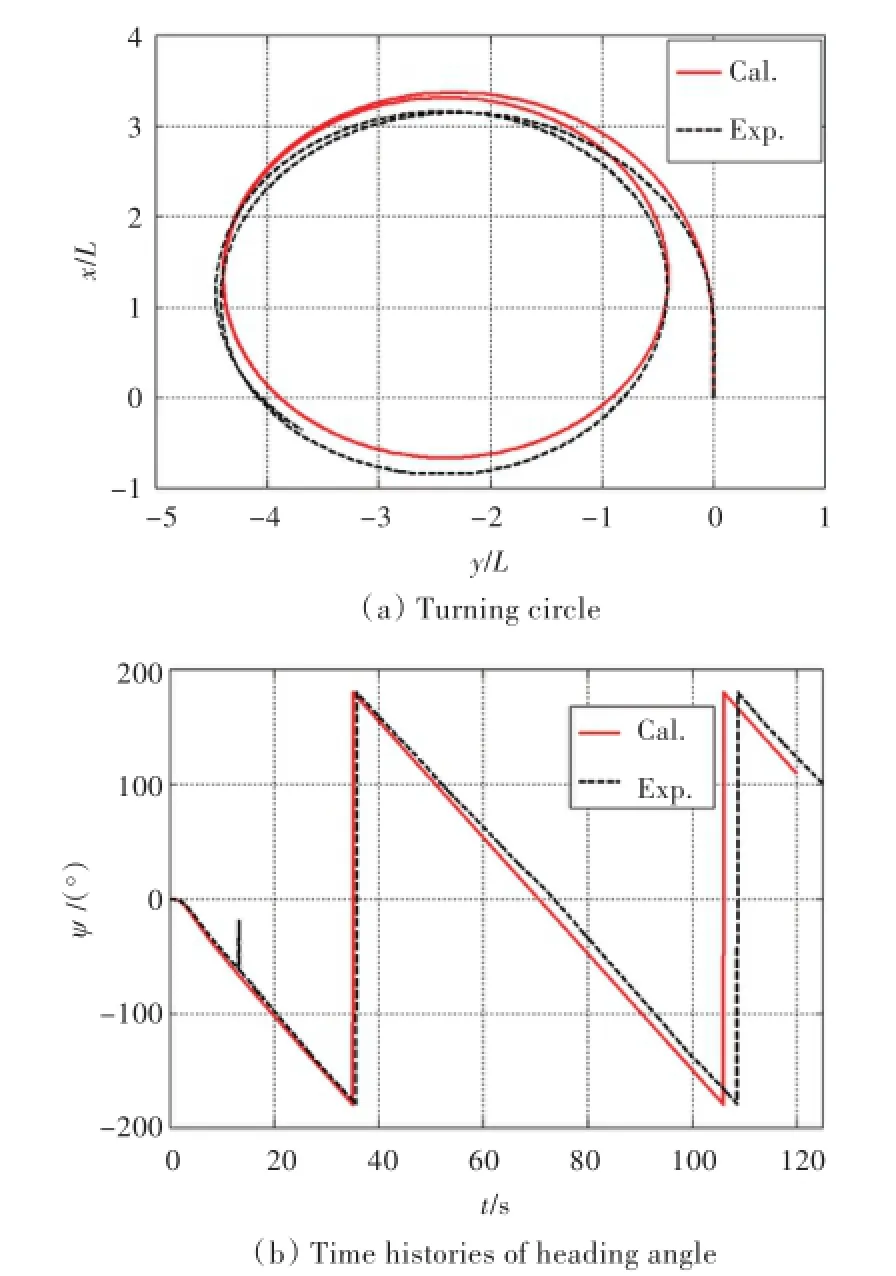
图8　左舵回转及艏向角时历Fig.8　Turning circle and time histories of heading angle in left rudder test

图9右舵回转及艏向角时历Fig.9　Turning circle and time histories of heading angle in right rudder test

考虑船舶在波浪中的回转特性，对船模进行迎浪规则波下回转运动的仿真，仿真条件为左舵35°，操舵速度13（°）/s，波浪工况与试航模试验部分相同。

图10～图12分别为在波浪工况W1，W2，W3下无因次回转及艏向角对比。计算结果与试验基本一致，验证了三维面元法计算波浪力具有一定的预报准确性。结果表明，在波频相同的情况下波高越大，船舶在纵向和横向的漂移越明显，且艏向角的跟踪误差变大。波高较小时，仿真的纵向漂移偏小，波浪力插值的精度偏低。

图10W1波浪工况下回转及艏向角时历Fig.10　Turning circle and time histories of heading angle in W1 wave condition

图11W2波浪工况回转及艏向角时历Fig.11　Turning circle and time histories of heading angle in W2 wave condition

图12　W3波浪工况回转及艏向角时历Fig.12　Turning circle and time histories of headingangle in W3 wave condition

3.2Z形仿真与验证

对船模进行静水Z形仿真，仿真条件为左右舵20°，操舵速度13（°）/s。并与自航模试验结果进行对比。

图13为左右舵Z形试验舵角及艏向角对比。由于水池尺度限制，试验只测量了第1超越角，计算结果的第2超越角略小于第1超越角。左舵计算的第1超越角略小于试验值，总体仿真与试验具有较好的一致性。

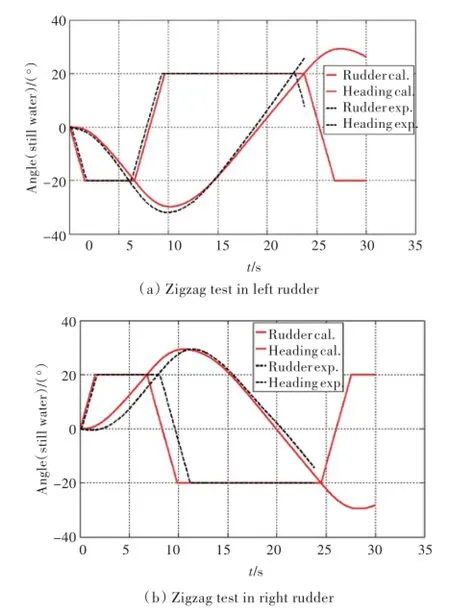
图13　左右舵Z形舵角及艏向角时历Fig.13　Time histories of rudder and heading angle in left and right zigzag test

考虑船舶在波浪中的Z形操纵，对船模进行迎浪规则波下Z形运动的仿真，仿真条件为左舵35°，操舵速度13（°）/s，波浪工况与自航模试验部分相同。

图14依次为W1，W2，W3波浪工况下Z形试验舵角及艏向角对比。与静水相同，试验只测量了第1超越角。结果表明，在相同波频时，波高越大，船舶所受的二阶漂移力越大，在相同舵效下，船舶改变航迹和航向的能力越低，所以第1超越角和第2超越角相对越大，同时，达到超越角的时间变长。

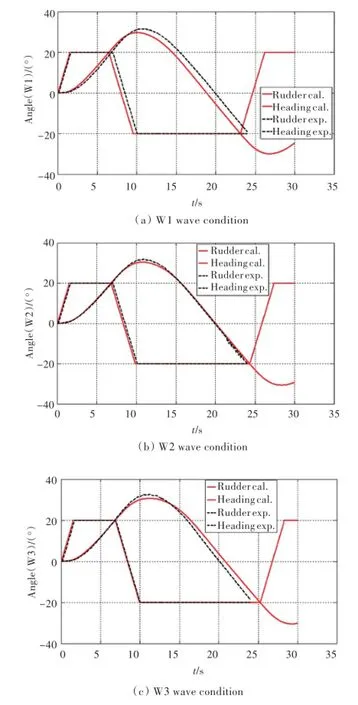
图14　不同波浪工况下右舵Z形舵角及艏向角时历Fig.14　Time histories of rudder and heading angle in right zigza test under different wave conditions

4　结论

本文结合统一理论和MMG模型，建立了操纵和横摇四自由度耦合模型，对船舶的回转和Z形操纵运动进行仿真预报，并开展自航模试验进行

验证。得出以下结论：

1）仿真和试验结果有较好的一致性，说明将统一理论和MMG模型结合能有效地预报船舶静水和波浪中的操纵特性。波浪中操纵船舶轨迹和航向随时间变长逐渐偏离实际情况，仿真预报的精度随时间降低。

2）船舶所受波浪力与船体自身运动和波浪运动有关，根据船舶实时速度和遭遇浪向进行二维插值获取，是一种波浪运动与船舶运动实时双向耦合的处理方法。计算结果表明，波浪力插值在波高较大时精度较高，波高较小时计算的回转漂移由于插值精度的降低而偏小。

3）波频相同时，船舶在波高越大的波浪工况下，纵向和横向的回转漂移均越明显，利用模型预报的艏向角较模型试验的偏差会增大，在Z形试验中则超越角越大，达到超越角的时间也更长。

［1］DAVIDSON K S M.The steering of ships in following seas［C］//Proceedings of Sixth International Confer⁃ence for Applied Mechanics，1948：554-568.

［2］KIJIMA K，FURUKAWA K Y.Ship maneuvering per⁃formanceinwaves［C］//3rdInternationalStability Workshop，1997.

［3］HAMAMOTO M，SHIRAI T.Study on ship motions and capsizing in following seas（2nd report：simulation of capsizing）［J］.Journal of the Society of Naval Archi⁃tects of Japan，1989，165（6）：123-130.

［4］YASUKAWA H.Simulations of ship maneuvering in waves（1st report：turing motion）［J］.Journal of the Ship and Ocean Engineering Society of Japan，2006（4）：127-136.

［5］AYAZ Z，VASSALOS D，SPYROU K.Maneuvering behavior of ships in extreme astern seas［J］.Journal of Ocean Engineering，2006（33）：2381-2434.

［6］NONAKA K.On the maneuvering motion of a ship in waves［J］.Transaction of the West Japan Society of Na⁃val Architects，1990（80）：73-86.

［7］SKEJIC R，FALTINSEN O M.A unified seakeeping and maneuvering analysis of ships in regular waves［J］. Journal of Marine Science and Technology，2008，13（4）：371-394.

［8］徐静，顾解忡，马宁.规则波六自由度回转运动预报［J］.中国舰船研究，2014，9（3）：20-27. XU Jing，GU Xiechong，MA Ning.Simulation of 6-DOF turning motions in regular waves［J］.Chinese Journal of Ship Research，2014，9（3）：20-27.

［9］盛振邦，刘应中.船舶原理［M］.上海：上海交通大学出版社，2009.

［10］贾欣乐，杨盐生.船舶运动数学模型—机理建模与辨识建模［M］.大连：大连海事大学出版社，1999.

［责任编辑：胡文莉］

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1201.007.html

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1201.006.html

Numerical Prediction and Free-Running Model Validation of Ship Maneuvering in Waves

ZHU Dongjian1，MA Ning1，2，GU Xiechong1，2，DENG Deheng1，2
1 School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，Shanghai，200240 2 State Key Laboratory of Marine Engineering，Shanghai，200240

A coupled 4-DOF model considering the 3-DOF plane maneuvering of sway，surge，yaw and roll is established in this paper based on the unified theory.The various forces on the ship are divided into hull，propeller，and rudder force according to MMG model.Then，ship maneuvering in waves is predicted by adding the wave force into the coupling model，where the wave force is interpolated with both the ship in⁃stant speed and the wave encounter angle，which are obtained through 3D panel method.The presented nu⁃merical model is validated through free-running model tests，and ship maneuvering in different wave con⁃ditions is predicted with the mean second wave force proved to be the main cause ship drifting in turning. The maneuverability of ships in waves due to different wave height is also discussed.The results show that greater wave height could lead to more severe ship drifting in both transverse and longitudinal directions.In addition，the first overshoot angle is larger and the lagging time is longer in the zigzag test.

maneuverability；free-runningmodeltest；MMGmodel；unifiedtheory；time-domainsimulation

U661.33

A

10.3969/j.issn.1673-3185.2015.01.011

2014-07-02

网络出版时间：2015-1-28 12:01

教育部财政部重大科研专项——船舶数字化智能设计系统二期

朱冬健，男，1990年生，硕士生。研究方向：船舶在波浪上的操纵与控制。E⁃mail：tobya@sjtu.edu.cn

马宁（通信作者），男，1961年生，博士，教授。研究方向：船舶与海洋结构物耐波性及安全性、海洋波浪数值模拟预报。E⁃mail：ningma@sjtu.edu.cn