船体结构砰击总体载荷理论研究综述

汪雪良，杨　鹏，顾学康，胡嘉骏

船体结构砰击总体载荷理论研究综述

汪雪良，杨鹏，顾学康，胡嘉骏

中国船舶科学研究中心，江苏无锡214082

船体结构遭受的波浪砰击载荷是一种强非线性的流体与结构之间的相互作用。砰击将导致船体主要按其两节点湿谐振频率发生振动，这种船体梁的总振动即为颤振。它往往引起船体结构的极限强度问题和疲劳损伤问题，这两种问题在船舶结构设计领域不可回避。从理论研究方面对船舶的砰击总体载荷进行综述，分析二维理论和三维理论在预报船体结构砰击总体载荷方面的优缺点。分析表明：虽然二维理论在该领域的应用已超过50年，但理论中基本假设和数学模型的局限性制约了其在肥大型船、多体船和海洋平台等领域的广泛应用；三维理论能突破二维理论的基本假设和数学模型的局限性，能在更加广泛的工程领域内得到应用。考虑外飘等非线性影响的三维时域水弹性理论能更加精确地预报砰击载荷，是船体结构砰击总体载荷理论研究的重要发展方向之一。

船体结构；砰击；颤振；船舶水弹性理论

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1204.014.html

期刊网址：www.ship-research.com

引用格式：汪雪良，杨鹏，顾学康，等.船体结构砰击总体载荷理论研究综述［J］.中国舰船研究，2015，10（1）：7-18. WANG Xueliang，YANG Peng，GU Xuekang，et al.Review of the theoretical investigation of slamming of global wave loads on ship structures［J］.Chinese Journal of Ship Research，2015，10（1）：7-18.

0　引言

船舶在恶劣海况中航行时，由于自身的大幅摇荡运动，船舶与水面之间的相对运动一般在船舶的端部达到最大，船体底部出水后的再入水可能会导致船体底部击打水的表面而引起明显的冲击或拍击，这种现象称为砰击（Slamming），大多发生在船底和舷侧等位置，此外还有艏艉柱砰击、高速双体船的湿甲板砰击以及甲板上浪等，大型工程船舶还可能发生舷侧平台的砰击。船体艏外飘砰击即使在底部龙骨没有出水时也会发生。这些砰击可能严重到足以导致船舶结构的局部损伤。即使中等的砰击也将导致船体按其两节点湿谐振频率发生振动，这种砰击导致的船体结构总振动叫颤振（Whipping）。颤振可导致船体结构的疲劳损伤［1］和总体强度［2］两个方面的问题。从中等海况到极端情况，砰击载荷使得波浪载荷的非线性程度显著增大，足够对船体结构造成永久性破坏。根据初步调查结果，2013年6月在也门外海断裂沉没的MOL Comfort号集装箱船就是因为波浪中的砰击载荷作用导致船体在中部发生断裂而沉没［3］。

总体而言，船体结构砰击是一种流体与结构之间持续时间短暂的相互作用。广义上，这种相互作用问题可以用Xing等［4］对流固耦合问题的一般性描述来求解。对船舶砰击载荷的研究可以从理论、模型试验和实船测试这3个层面开展。本文主要对船舶总体砰击载荷的理论发展进行综述，并在最后对相关研究进行展望。

1　二维理论

1.1切片理论及Wagner入水砰击理论的发展

随着耐波性领域中二维切片理论的引入，Korvin-Kroukovsky［5］，Salvesen［6］，Faltinsen［7］以及Bishop［8-9］等就二维船舶水弹性的对称响应和反对称响应理论问题进行了多方面的探讨与广泛的数值分析研究工作，把船舶耐波性理论和结构动力学结合在一起，建立了二维水弹性力学理论。为了在数值分析中表现船体梁的弹性，船体经常简化为一根梁模型。通常采用几种梁理论，如Euler-Bernoulli梁、Timoshenko梁或Vlasov梁理论。Bishop等［9］讨论了分析结构动态响应的一些方法，并得出了“模态分析能提供最好回报”的结论。从此，这种方法得到了广泛的应用。流体简化为二维流场，建立流固耦合运动方程，以船体在“真空”中的干模态为广义坐标，对船体的振动进行模态分析，可以给出船体梁各个截面的动位移、波浪载荷和结构动响应。该理论可以用来分析船体砰击颤振响应以及波激振动问题。

从上世纪70年代末开始，基于二维线性水弹性理论对船舶砰击载荷的预报理论得到了一定的发展和应用，瞬时湿表面等非线性影响开始计入到理论预报之中。Belik等［10-11］进行了弹性船体在不规则波中迎浪航行时砰击响应的时域模拟；Clarke［12］分析了某护卫舰由波浪激励以及砰击诱导的结构动响应。Yamamoto等［13］较早进行了非线性水弹性研究，计入了瞬时湿表面的影响，其在普通切片理论的基础上，将切片上的流体附加质量和附加阻尼表示为时间的函数，并考虑附加质量的变化率所引起的砰击力。Yamamoto等［14］基于上述理论，对5 000 m×840 m的水上浮动机场的概念设计方案进行了非线性水弹性动响应分析。Wu和Moan［15］发展了二维非线性水弹性理论，将整体响应分成两部分：线性部分利用势流在频域范围分析；非线性部分由线性船舶流体作用系统的脉冲响应函数的卷积和非线性水动力组成，并且包括了自由表面记忆效应以及动量砰击力成分。

为了在水弹性方法中计入非线性动量砰击力及非线性静回复力的影响，Gu等［16］从二维势流理论出发，推导了一个带有卷积的时域广义切片理论。Soding［17］建立了相对速度与相应水动力之间的高阶微分关系，计入了由自由面引起的记忆效应。Xia等［18-19］引入这一关系导出微分形式的水弹性理论，在推导出的非线性时域切片理论中，直接包括了动量砰击力以及由自由表面引起的水动力记忆效应，水动力惯性力以及回复力在瞬时湿表面上处理，在水弹性方程中求解了船舶的结构响应。该方法可用于预报在中等海况中航行舰船遭受的波浪及砰击载荷，理论分析结果与Watanabe等［20］获得的S-175集装箱船试验结果做了比较，吻合较好。

上世纪90年代中期以后，非线性二维水弹性理论得到了进一步的发展，理论预报中可以考虑多种非线性因素的影响。任慧龙［21］考虑到底部砰击、外飘砰击和甲板上浪的影响，根据水弹性理论建立了舰船在迎浪及斜浪中的非线性运动方程，并计算了相应的波浪载荷。该理论以线性频域切片理论为基础，用Fourier展开式表示非线性载荷与其对应运动的关系。在不规则波情况下，用船舶重心处的波面升高时间历程中每个跨零周期所对应的频率作为计算该时间段内船体剖面水动力系数的频率参数。对一艘超大型油轮的数值分析表明，是否计入船体弹性变形所获得的船舯弯矩相差12%～20%，因而对这类船舶需要考虑其水弹性作用。Faltinsen［22］在波浪载荷的研究中强调了水弹性的作用，通过引入初始的结构惯性相位和随后的自由振动相位对问题的简化，采用水弹性梁模型从理论上研究了湿甲板的砰击。该理论考虑了航速效应。理论模型通过与波浪中弹性板的落体试验结果的比较得到了验证。板上的应力与冲击速度成线性关系，但对波浪的曲率半径和初始的撞击位置并不敏感。作者认为考虑水弹性很重要。即使是在确定的环境条件下，最大冲击压力也能达到非常大，表现出很强的随机性。但这些冲击压力对最大弯曲应力来说并不重要。

Park等［23］对在恶劣海况下航行的船舶水动力的弹性响应分析考虑了砰击载荷的作用。为了获得船体梁的颤振响应，采用了Yamamoto等［13］的方法。该方法根据Timoshenko梁理论把船体结构模型化为弹性体的有限元模型。采用动量砰击理论导出非线性水动力载荷，这种非线性考虑了自由表面与船体表面之间的相互作用。在他们的程序中可以得到各种各样的设计信息，诸如涉及砰击效应的各剖面相对位移、相对速度、相对加速度、垂向剪力和垂向弯矩的时间历程。作者仅考虑了顶浪工况，但考虑了大幅波浪作用下每一个时间步长上水下实际船体的剖面形状，水下部分的非线性边界条件得到了满足。在实际海洋环境中，斜浪向下的砰击载荷的特性较顶浪向的复杂，需要考虑横向载荷和扭转载荷的作用，仅考虑垂向弹性变形的Timoshenko梁理论不能满足上述要求。

为在理论预报中考虑底部砰击、艏外飘和甲板上浪对弯矩的综合影响，Gu等［24］发展了一个恶劣海况下预报船体运动和结构响应的非线性时域切片理论。船体梁的弹性模态根据Timoshenko梁理论进行计算。为验证预报的结果，开展了一条船在规则波与不规则波中的模型试验，船模模拟了艏外飘和低弯曲刚度。比较显示，模型计算结果与试验结果吻合很好。高阶谐振与垂向弯矩中的颤振成分之间的耦合效应在数值计算中得到了证实。对两种艏外飘船型的S-175集装箱船也进行了理论计算与模型试验的比较研究。讨论了颤振的原因及模型试验结果与理论计算结果之间的差异。良好的预报性能和计算效率使得该理论及程序能用于长期的非线性弯矩的直接计算。

Faltinsen等［25］对船舶与海洋结构物的实际砰击问题进行了简要描述，主要阐述了静水面入水、湿甲板砰击、甲板上浪和晃荡现象的理论状态与未来的发展。文中强调砰击应该在结构动态响应的整个框架下考虑，综合分析船舶与海洋结构物周围的整个流场以及舱内的流体晃荡。两相流可能会带来重要的载荷影响，需要对此深入理解。

为了在二维理论预报中计入三维的影响，Hermundstad和Moan［26］给出了考虑三维效应的修正的船体砰击载荷的预报方法，并以一艘航速为20 kn、长度为120 m的运车船作为算例进行了验证。采用非线性切片理论计算船舶和波浪的相对运动。在砰击计算中考虑了一次砰击事件中的相对速度和横摇速度，这里的理论采用广义二维Wagner公式，并用边界元法求解。这种方法计算速度快、精度高。研究发现，由船舶速度导致的艏部周围的堆水作用显著增大了砰击压力。计算的砰击压力根据三维效应进行修正后，数值计算结果与模型试验结果吻合较好。由于速度对波高的影响与三维流体作用的影响方向相反，因而包含这两种影响的数值计算结果与模型试验结果也符合较好，尤其是在发生最严重砰击事件的时候。

为评估水弹性分析方法在确定船舶结构设计载荷中的作用，El Moctar［27］，Schellin［28］和Ober⁃hagemann［29］等发展了一种总体设计载荷的预报方法。该方法首先用一种频域面元法得到船舶上易于发生砰击剖面的相对运动的传递函数，然后在设计波下对相对运动进行长期预报。在雷诺平均纳维斯托克斯（RANS）模拟［27，29］中或者在非线性切片方法［28］中使用设计波，以计算非线性船舶运动。RANS模拟中生成的压力可用于有限元模型，以预报单向耦合系统中砰击导致的颤振响应。采用Lewis剖面［9］生成分布在有限元上的附加质量。对非线性切片理论来说，计算得到的非线性船舶运动可用于RANS模拟以获得设计压力。这些压力由模型试验得到了验证，并与设计规范值进行了比较。比较发现设计规范值偏低，这表明在应用设计规范恰当地评估设计载荷时应用流固耦合方法很有必要。

关于预报不规则波中船体砰击压力的有效方法，Hermundstad和Moan［30］采用基于Zhao等［31］提出的广义二维Wagner公式表达的二维边界元法，以一艘290 m的游轮作为算例进行了验证。船和波的相对运动采用非线性切片理论进行计算。为了提高理论的计算效率，在砰击计算中考虑了一次砰击事件中的相对速度和横摇速度。这种方法分成2步：第1步是为剖面和水之间的单位相对速度计算速度势；第2步，这些预先计算的速度势和航行时的实际相对速度结合，用来计算剖面上的砰击压力和总的砰击力。这样在进行不规则波中的砰击计算时能节省可观的计算时间，并且计算精度没有明显的损失。游轮艏外飘砰击压力的计算值与试验测量值吻合较好，尤其是计算的和试验的运动结果在时间窗口上符合很好。文中还给出了不规则波中每个船体剖面上瞬时峰值压力的简化计算方法。采用这种方法来确定砰击事件，可用于更加精确的二维边界元方法的分析。与试验测量值的比较表明，该方法还可用来快速评估最大砰击压力。

通过采用二维非线性切片理论和模型试验，Wang等［32］对一艘超大型油轮的砰击载荷进行了比较研究，分析了装载状态对砰击载荷的影响，发现压载状态下砰击载荷的相对值和绝对值均较满载时的大。另一方面，理论计算的中垂和中拱的差异较试验值小，这说明理论计算中考虑的非线性成分并没有完全反映模型试验遭遇的非线性影响。

1.2二维刚体和弹性船体混合理论的发展

海上航行船舶发生砰击事件时的海况往往是中高海况，这时的船舶运动就是一种大幅运动。然而，船舶结构刚度的制约使得船舶的变形是小量，这就使得在船舶砰击载荷的理论预报中有必要结合大幅运动和小船体变形的特点。为此，Wu和Moan［15］发展了预报波浪中大幅运动和小船体变形时波浪引起的垂向运动和载荷的非线性理论预报方法。在这种方法中，船体建模为一根Vlasov梁，船体变形近似为弹性模态的叠加。通过模态叠加法得到波浪引起的船舶响应。垂向运动和横剖面载荷的非线性效应通过非线性激励力来引入。在该方法中，船舶运动或载荷效应与激励力之间的关系可仍然保持为线性，由于与入射波相关，激励力则不再为线性。总的非线性激励力由线性部分和非线性部分组成。线性部分由二维或二维半切片理论来计算，非线性的修正部分则由线性脉冲响应函数的卷积以及非线性的修正力来得到。非线性效应包含了砰击冲击力、非线性入射波力和非线性静水回复力。

通过将总弹性模态分为动态和准静态两个部分，Wu和Hermundstad［33］进一步改进了Wu和Moan［15］提出的方法，这样可以减少非线性模拟的计算时间，而结构的动态效应仍然得到了考虑。Wu和Hermundstad［33］比较了S-175集装箱船的计算结果和O'Dea等［34］的模型试验结果，发现试验测得的与理论预报的垂向运动结果符合得非常好。完全非线性的三维理论结果［35］在大多数情况下和二维预报结果接近。虽然该方法倾向于低估船艏部分的中垂弯矩，但是二维程序计算得到的顶浪规则波中弯矩的中垂和中拱与测量结果仍然吻合得很好。

尽管将总弹性模态分成动态和准静态两个部分能减少计算时间，然而仍有必要确定所需要的总弹性模态的阶数。该阶数在不同船舶之间以及不同响应之间会有所不同，仅能通过收敛性确定，这种收敛性应该在每一种响应上实现。应该注意的是，有时很难确定计算是否达到了收敛。Wu和Moan［36］扩展了文献［15］和文献［33］的方法，该扩展方法是一种波浪诱导的船舶响应（wave-in⁃duced ship responses，WINSIR）混合法，可用于计算水弹性响应。

1.2.1WINSIR混合法

WINSIR混合法是传统的刚体直接载荷计算评估和弹性船体模态叠加相结合的方法。根据模态叠加法计算得到的最低阶总弹性模态中的动态影响可加入到传统的载荷计算方法中。系统采用右手坐标系，原点固定在未受扰动的自由表面上。z轴通过重心垂直向上，x轴指向船尾。广义运动的方程为

式中：p（t）包含6+N部分，前6个描述刚体的运动，剩余的N个描述弹性模态；A，B和R分别为广义的流体附加质量、阻尼和静水回复力矩阵；M，C和K如式（2）所示。

式中：MR和KR为六自由度刚体运动模态的质量和重量矩阵，重量矩阵的引入是为了考虑加速度的瞬时相对方向，通过平均湿表面上单位法向静水压力的积分得到回复力矩阵；MF，CF和KF分别为弹性模态的质量、阻尼和刚度矩阵。总阻尼包括内部结构阻尼和线性水动力阻尼。与相对运动相关的粘性效应的影响［37］和航速对阻尼比的影响没有完全计入到WINSIR混合法中。总的非线性激励力f（t）由线性部分f1（t）和非线性修正部分fnm（t）组成，即

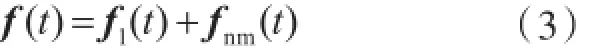
向量fnm（t）的第k部分的形式如下：

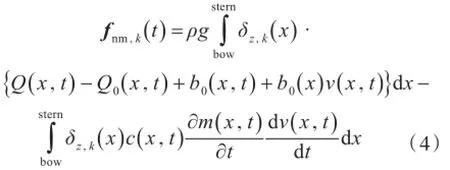
式中：δz，k（x）为模态k时横剖面形心的垂向位移，对垂荡和纵摇，和 Q0（x，t）分别指横剖面的瞬时和平均湿表面面积；b0（x）为平均吃水处的横剖面宽度；c（x，t）为修正因子；m（x，t）为瞬时浸没横剖面不计水的堆叠影响的高频附加质量；ν（x，t）为船体相对于波浪表面的垂向位移。这里的力中没有计入辐射波和绕射波的影响。

式（4）中的第1个积分是Froude-Krylov力和静水回复力的非线性修正，第2个积分则表示砰击力。砰击力在出水的过程中被忽略。堆叠水的影响则根据修正因子c（x，t）近似地计入，它是波浪表面遇到船体表面时船体型线上该点的正切函数。修正因子的依据是Zhao等［31］对不同攻角下楔形体入水砰击的研究结果。他们给出了基于Wagner方法的解决途径，研究表明，该方法对总体砰击力和局部砰击力都能有合理的近似。Hermundstad和Moan［26］采用广义的Wagner方法计算了一艘滚装船的艏外飘砰击载荷，计算得到的考虑三维效应修正后的砰击压力与测量得到的结果符合很好。Wu和Moan［36］采用的堆叠水修正因子以一种比值的形式给出，它为采用广义Wagner方法得到的垂向砰击力与不考虑堆叠水的冲量砰击得到的垂向砰击力之间的比值。然而一般来说，二维计算得到的砰击力太大，这主要是由于艏部的面积不是二维造成的。

关于非线性，WINSIR混合法确实没有考虑流体压力Bernoulli方程中的二阶速度项。因而该程序仅能计算一阶速度势，不能预报二阶压力场，在特定的情况下，这些二阶压力场将以和频的形式不依赖于水深而振荡。这两种特征在Jensen和Dogliani［38］的二阶切片理论中得到了考虑，它们会导致显著的非线性波激振动［39-40］。WINSIR混合法也没有考虑船体周围由于前进航速造成的定常波浪的影响。

为了验证他们的混合方法，Wu和Moan［36］比较了混合法与传统直接响应计算方法得到的船舶垂向弯矩的传递函数。比较中采用的船舶为SL-7集装箱船。混合法中采用弹性船体，传统的方法则采用刚性船体。在相关的频率范围内，混合法得到的结果比传统计算方法得到的结果要小很多。Wu和Moan［36］将他们的计算结果与试验结果进行了比较。试验在荷兰船舶研究中心（TNO）进行。模型是玻璃钢船模，缩尺为1∶55，分成4个刚体分段，用3个五分力应变传感器进行连接。分段剖面为第5，10和15站，并用弹性胶带进行密封。试验进行了7个浪向，在每个浪向下有7个规则波。比较发现，预报的一阶非线性谐振弯矩与试验值很吻合。这种混合法的应用能在保证计算精度的前提下大大提高计算效率。

1.2.2极端载荷影响

从直接载荷计算评估特定船舶响应生命期内的极端载荷，最直接的方式是长期预报分析。通过所有可能的波浪峰值周期、有义波高、浪向角和航速下的短期预报的求和，可以得到长期预报的峰值分布。最大值R̂超过r的长期概率为：

式中：ωˉ为权函数，表示每个海况下峰值响应的相对率；fHs，Tp，U，β（h，t，u，β）为有义波高、峰值周期、航速和浪向的联合长期概率分布函数；为短期的累积概率分布。当采用线性理论时，响应满足高斯分布。并且，假设窄带响应可用Rayleigh分布描述。响应的变化可从船舶在特定海况下的传递函数和波浪谱中得到［41-42］。

在确定某些船舶，尤其是有艏外飘船舶的设计载荷时，应该计入非线性的影响。如果计入了非线性的影响，则累积概率分布不再服从Ray⁃leigh分布，此时，应用Weibull分布来代替。采用Weibull分布，超过r的响应最大值的短期概率分布为

上述分布中，参数的精确确定需要对每个特定海况进行长时间的非线性模拟或者模型试验，特别是该分布的尾部是研究主要感兴趣的部分，因此形成了很多简化的方法来解决这个问题，ISSC［43］对这些方法进行了讨论。

例如，Guedes等［44］计算了一艘快速单体船在北海北部海域25年期间由波浪引起的垂向弯矩的最大值。他们假设服从Ray⁃ leigh分布。用于计算短期响应的非线性的伪传递函数（Pseudo-Transfer Functions）根据Fonseca和Guedes［45-46］的非线性程序计算得到。他们通过规则波中的传递函数来考虑非线性的影响，规则波的波高等于实际海况的有义波高。另外一种做法是应用贡献系数法［47］，这种方法可确定对极端载荷海况贡献最大的海况，并在长期预报中得到应用。Baarholm和Moan［47］对海洋结构物通过几种短期海况进行长期载荷分析，认为可用这几种短期海况替代海浪散布图中所有海况的响应计算。

Winterstein等［48］给出了海洋结构物的某种响应超过一定概率的计算方法。Baarholm和Moan［49］应用这种方法鉴别了（Hs，Tp）平面上一系列海况的等高线。他们提出了一种用这些海况确定一个平均重现周期（D-year）时响应的方法，这种方法的优点是环境分析和响应分析不耦合。该文［49］给出了用这种方法获得的极端载荷，与QLT（r）公式的计算结果很接近。然而，该计算仅基于波浪频率范围，不含高频效应。Barrholm和Jensen［50］证实了这种等高线方法，考虑了砰击的影响，研究认为这种方法能给出长期极端载荷较满意的结果。

1.2.3小结

二维理论对砰击载荷的预报在国际上已较成熟，并且各研究机构也已发展出了各自的预报方法。这些方法大都是在Wagner理论的基础上发展而来，具有较广泛的理论和应用基础。然而，该类理论原始假设的局限性制约了其在肥大船型、多体船型和海洋平台等船舶与海洋工程领域的广泛应用。

2　三维理论

尽管二维水弹性理论在船舶结构工程中得到了大量应用，但是由于其理论局限性，仅适用于细长型船体，不能计及船体艏艉的三维效应，在肥大船、多体船和半潜式平台等船舶与海洋结构物领域的应用受到了制约。过去30年来，许多研究人员开始采用三维理论研究船舶与海洋结构物在波浪中遭受的载荷及结构动响应。

2.1频域理论

一般来说，砰击载荷作为一种高频瞬时冲击响应，理论预报需要在时域上进行，这里给出的频域理论扼要介绍了船舶水弹性理论的发展过程，文献中描述的非线性因素也需要在砰击载荷的时域理论预报中加以考虑。

上世纪80年代，三维船舶水弹性理论得到了实质性的发展，基于三维耐波性理论和三维结构动力学理论的结合，Wu［51］和Price等［52］提出了广义的流固界面条件及围绕弹性体的三维势流理论，从而形成了一个适用于在波浪中航行或水下运动的任意形状弹性体的三维线性水弹性力学理论。进一步地，为把流固耦合的界面条件进行一般化推广，Wu［53］给出了计及物面应变张量影响的流固耦合交界面的一般形式。当弹性体表面无切向外力时，该条件即为广义流固界面条件，也称为Price-Wu条件［52］；当结构为刚体时，它就成为刚性流固界面的Timman-Newman条件［54］。自此，刚体结构和弹性结构的流固界面条件的描述实现了统一。

上世纪90年代以后，为了提高三维水弹性分析工作的速度和效率，杜双兴［55］和Wu等［56］发展了零航速三维振荡源Green函数快速计算方法，使得三维水弹性分析工作可以在微机中运行。为计入航速的效应，杜双兴［57］建立了完善的三维航行船体线性水弹性力学频域分析方法。进一步地，非线性因素开始逐渐在三维水弹性理论中得到考虑，Wu等［58］提出了考虑二阶水动力作用的三维非线性水弹性理论。该理论考虑航速和定常兴波流场的影响，并计及大角度刚体运动和瞬时湿表面变化对非线性波浪力的贡献，建立了大浪中航行船舶的三维非线性水弹性力学分析方法。在上述基础上，Tian和Wu［59］、田超［60］等进一步发展了有航速的三维非线性水弹性理论，考虑波浪中航行浮体周围流场的一阶速度势及其一阶响应对二阶水动力的贡献，推导了大浪中航行船舶的广义二阶非线性水弹性理论，并给出了广义三维非线性水弹性运动方程中二阶波浪作用力的水动力系数表达式。

近年来，散货船相对较高的海事事故率以及诸如甲板大开口等结构特征，使得这类船舶成为用水弹性模型预报波浪诱导载荷和响应的适合船型。由于二维和三维的流体—弹性结构相互作用对模型复杂程度和数据要求不同，在评估波浪诱导载荷时，它们可用于设计过程的不同阶段，即初始设计阶段和详细设计阶段。通过应用二维和三维水弹性理论对一艘散货船在波浪中的动响应进行预报和比较，Hirdaris等［61］分别研究了船舶对称和反对称的运动及变形。三维结构模型为包含所有主要外部和内部结构组件的有限元模型，而二维模型则为Timoshenko梁的有限元模型。文中讨论了和结构建模阶段相关的一些问题。对真空中模态的动态特性进行了比较，特别强调了结构中舱口开口、剪切中心和反对称动态翘曲的影响。在流体—弹性结构相互作用的湿模态分析中，二维方法采用Timoshenko梁和切片理论，三维方法采用理想化的梁和壳单元并结合基于在平均湿表面上分布脉动源的势流理论。对艏斜浪规则波中的稳态响应在二维和三维模型下的预报结果进行了比较，比较表明两者预报的对称动响应符合较好，而反对称动响应之间则存在着差异。这可能是由于梁模型对非棱形船体梁的总动响应的预报能力不足，因为此时需要考虑船体梁的翘曲效应。

2.2时域理论

从时域上采用三维水弹性理论进行砰击载荷的预报是近20多年来很多专家学者的研究目标，近年来，也受到了DNV-GL，BV和LR等几大船级社的关注，他们都投入了相当的人力和物力来发展这方面的理论及其应用。时域方法是直接在时域内建立初边值求解问题，与频域方法相比，时域方法在处理诸如砰击等瞬态问题方面具有频域无法替代的优势。

尽管二维和三维理论都能评估砰击导致瞬时载荷的影响，但两者的假设和数学模型不同。Aksu等［62］分别采用二维和三维理论对在规则波中航行的细长与非细长弹性体响应进行了研究。二维理论限制在顶浪规则波中稳态和瞬时的垂向响应（运动、变形、弯矩和剪力）的计算。而三维理论则允许计算顶浪和斜浪中的垂向和横向响应（运动、变形、弯矩、剪力和扭转）。两种理论均根据统计数据生成响应（稳态和瞬变）的时域模拟。对于一艘顶浪航行的细长均匀驳船，两种理论对响应的模拟和统计数据的评估显示了两者之间符合很好。然而，对非细长均匀驳船的计算表明，在两者之间存在着较大的差别，这是由于二维切片最终不适用于计算，而三维方法仍然有效，并且显示出了任意浪向下不规则波中弹性驳船结构砰击行为的预报能力。在三维砰击压力的计算中，由于计算耗时的问题没有采用Leibowitz动量理论，仅采用了Stavovy和Chuang冲击理论。尽管文中作者提到其他文献已经说明这两种理论得到的瞬时响应的量级类似，但这篇文章发表在上世纪90年代初，与当今计算机的计算能力相比不可同日而语，因而现在可尝试使用Leibowitz动量理论进行三维砰击压力的计算。

为揭示砰击和上浪等非线性瞬态作用导致冲荡响应的力学机理，王朝晖等［63］从入射波的波浪现实出发，用非线性水弹性积分—微分法进行了船体运动和结构动响应的时间历程模拟，直接将试验测量与理论计算结果在时域内做比较。这种模拟及其验证方法避免了在对理论和试验结果的统计特性进行比较时，因子样长度的限制和数据处理过程所带来的不确定性，比峰值的比较更能说明波激响应数学模型的精确性和可靠性。

根据弹性浮体流固交界面的Price-Wu条件，王大云等［64-65］利用三维时域Green函数，给出了围绕弹性体的三维势流时域积分方程。在时域上求解于波浪中航行的弹性结构周围的三维势流方法可以表达为一个边界积分方程，其中在与时间相关的问题上，Green函数满足线性自由表面条件。在时域上可直接预报船舶以稳定航速航行时的载荷、运动和结构响应。通过时域预报结果和模型试验结果以及频域预报结果的比较表明，采用Ham⁃ilton系统精细积分算法能提高船舶结构在波浪中运动变形的时域响应数值计算的效率和精度。

基于水动力中包含记忆效应卷积的二阶广义微分，Kashiwagi［66］给出了任意与时间相关的外部载荷的弹性响应的时域计算方法。依赖于时间的结构弹性挠度用数学上模态函数的叠加来表达，根据假设的模态函数幅值，用Galerkin方法得到了微分方程模拟的线性系统。对计算记忆效应函数和无限频率时附加质量的数值精度给予了特别关注。通过与落体冲击试验中垂向挠度结果的比较，以及与同样问题已有数值计算结果的比较，验证了数值计算结果的有效性。为了检查记忆效应项的必要性，对水动力阻尼系数取值为常数时也进行了计算，讨论了减少计算时间的实际措施。

为了计入一阶速度势和一阶响应对二阶作用力的影响，陈徐均［67］推导了带航速浮体三维二阶非线性水弹性理论，分析了二阶水动力系数的广义形式，建立了航行浮体三维二阶水弹性分析理论。进一步地，陈徐均［68］研究了在高海况条件下浮体做大幅运动时由其刚体运动引起的二阶力以及由瞬时湿表面变化引起的二阶流体力，它们可能对浮体产生较大的非线性影响。当海洋浮体的尺度大为增加，远远超过常规船舶的尺度时，它们的低频特征十分显著，在波浪中的运动也会不同于一般的浮体。在这些情况下，就有必要研究二阶及以上波浪力对浮体水弹性响应的影响。作者建立了同时考虑流体和结构非线性因素的时域非线性水弹性理论，以同伦分析方法为基础给出了其求解方法。通过考虑结构非线性的水弹性分析，作者得出的主要结论是：对于大挠度变形的浮动平板，薄膜力对位移和弯矩以及应力都有一定的影响，薄膜力引起的最大非线性应力可达最大应力的30%左右，在设计过程中应该加以考虑。研究结论对于大型浮式结构物结构设计载荷的确定有一定的指导意义。

在波浪中弹性浮体结构水弹性响应时域数值方法的研究方面，Liu和Saka［69］采用边界元方法计算了流体的运动，采用有限元方法分析了结构的弹性变形。通过规定每一个时间步长上的波面边界条件和满足流固界面上压力和位移的连续性条件，该数值方法模拟了动态的波浪—结构相互作用。在预估—矫正法中通过时间步长的计算进行时域求解。空间和时间的离散化对求解收敛性和稳定性的影响在规则波、不规则波以及孤立波的情况下进行了数值比较分析。通过3种波浪条件下与模型试验结果的比较，数值方法的有效性得到了证实。在数值分析和模型试验中还观察到了孤立波在浮体结构下分裂的现象。孤立波在实际大洋中是存在的，并且可能会对船舶结构产生巨大的载荷作用，从而导致结构的灾难性破坏。

完全非线性的水动力学方法在三维时域水弹性理论中的应用使得总体波浪弯曲和砰击可同时进行模拟。Dominic等［70］在广义模态法处理刚体模态的基础上采用完全非线性的水动力学方法进行了总体波浪弯曲和砰击这两个方面的各非线性因素的分析。非线性流体求解器对砰击问题以及结合砰击问题的总体波浪弯曲问题的求解都很重要，之前，该领域的大多数研究人员都倾向于把砰击问题与总体载荷问题分开来求解，而该作者致力于在保持计算精度和可靠性的同时提高计算效率，因此该方法可作为船舶后期设计的有效工具，也能为将来设计准则的发展提供实用且精度高的信息。

总之，三维水弹性理论对砰击载荷的预报能避免二维理论的细长体假设局限，但三维理论对砰击载荷的预报需要更多地考虑瞬时冲击特性等非线性效应，并且需要在时域上分析流体与结构之间的相互作用关系，这将导致计算耗时急剧上升，因而三维水弹性理论在砰击载荷领域的发展还需要考虑计算效率的提高。

3　其他方法

其他研究船舶与海洋工程砰击载荷的方法还有有限元方法（FEM）、计算流体动力学（CFD）方法以及光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）方法等，在这些领域，都有研究人员进行了相应的研究。

Bereznitski和Kaminski［71］认为水弹性理论方面的研究越来越多，但是关于其在船舶设计中的实际意义的讨论很少，作者研究讨论了水弹性效应对船舶性能评估的影响。采用MSC/DYTRAN商业FEM软件，对一艘现代旅游船在船艉砰击条件下的水弹性作用进行了分析。工作的内容包括简化的水弹性模型分析，包含诸如砰击和局部船艉振动模态这些重要的船舶结构属性。仅在砰击位置详细建模以考虑水弹性的作用（模型包括船体梁、船舶砰击区域横向框架、空气域和水域），船体梁采用Timoshenko梁建模，这样整个模型就是结合局部结构详细有限元模型的杂交模型。文中考虑了以下几项船舶设计准则：乘客舒适性、船体梁总强度和局部强度。研究发现：用传统设计载荷计算方法得到的弯矩量值较考虑了水弹性效应的弯矩量值偏大33%；局部结构响应在考虑水弹性的耦合作用后，位移和应力也下降了30%，这说明水弹性效应对于结构设计载荷的确定将产生重大影响。这种分析方法的优势是大大减轻了结构建模的工作量，对船体内部结构详细资料的需求也大为减少，并能对结构的局部砰击响应进行详细的水弹性分析。

对江海直达船这种船型宽大、吃水浅的船舶，袁罡［72］利用FEM分析软件MSC.NASTRAN，基于模态分析法，对江海直达船在艏部砰击载荷作用下的船舶总体结构鞭击振动响应进行了相应的分析研究，刘正国［73］采用LS-DYNA软件也对该船型的总体砰击载荷进行了研究。这里所说的鞭击振动即由砰击引起的船体颤振。由于在分析过程中只是将附连水质量以质量单元的形式添加到相应的船体外板上，未考虑在砰击过程中船体变形对砰击载荷的影响，因而分析结果中水弹性的效应没有得到充分考虑。

El Moctar等［74］采用有限体积CFD方法和Timoshenko梁模型，进行了船舶砰击载荷的双向耦合模拟。该方法能预报不规则波中舯剖面的垂向弯矩，该文认为计算时间的需求限制了该方法在实际问题中的应用。随着高速计算机技术的发展，有理由相信CFD方法在船体结构砰击理论预报中的应用必定是未来发展方向之一。

SPH方法是近20多年来逐步发展起来的一种无网格方法，该方法的基本思想是将连续的流体（或固体）用相互作用的质点组来描述，各个质点上承载各种物理量，包括质量、速度等，通过求解质点组的动力学方程和跟踪每个质点的运动轨道，求得整个系统的力学行为。这类似于物理学中的粒子云（Particle-in-Cell）模拟，从原理上说，只要质点的数目足够多，就能精确地描述力学过程。虽然在SPH方法中解的精度也依赖于质点的排列，但它对点阵排列的要求远远低于网格的要求。由于质点之间不存在网格关系，因此它可避免极度大变形时网格扭曲而造成的精度破坏等问题，并且也能较方便地处理不同介质的交界面。SPH方法的优点还在于它是一种纯Lagrange方法，能避免Euler描述中Euler网格与材料的界面问题，因此特别适于求解高速碰撞等动态大变形问题。郑兴［75］以预报FPSO储油轮和半潜式平台的舷侧拍击及甲板上浪载荷为背景，对SPH方法进行了基本的理论研究。Sun［76］用SPH方法研究了楔形体的入水砰击问题，并与Zhao等［77］的试验结果进行了比较。作者比较了SPH方法数值计算结果和试验结果，发现楔形体的入水速度以及冲击压力都符合较好。作者还研究了不同参数的敏感性，包括楔形体的质量、初始入水速度和攻角这3个方面。虽然该文给出的砰击研究主要是针对局部砰击载荷，但是这种SPH方法在总体砰击载荷领域的发展与应用也值得关注。

4　结语

船舶与海洋结构物在波浪中遭受的砰击载荷属于非线性波浪载荷，其研究方法已得到了多年的发展，总体而言，有二维理论、三维理论、有限元、CFD和SPH方法等。本文主要针对二维理论和三维理论进行了详细综述，分析了它们在砰击领域的进展。目前，较成熟的理论大都基于Wagner入水砰击理论进行发展，文中重点对Wagner冲击理论、动量冲击理论以及WINSIR混合理论进行了描述与分析。三维理论则主要对时域理论进行了综述。

三维理论是砰击载荷发展的趋势所在，它能突破二维理论仅适用于细长体的局限性，除了常规的单体船型外，还适用于肥大船型、多体船型和海洋工程等结构物在波浪中砰击载荷的分析。然而，目前的三维理论关于船舶与海洋结构物遭受的砰击载荷的研究还不太完善，考虑的非线性因素也不充分，这对于表现为诸多非线性因素综合作用的流体和结构之间相互作用的砰击载荷来说远远不够。这些非线性因素主要包括物体湿表面和法向方向的变化、自由面非线性、砰击效应、甲板上浪等，这会导致浮体所受的静水回复力、入射波力、绕射波力和辐射波力出现非线性。因而结合二维理论中考虑砰击效应的成熟技术手段，重点开展三维时域非线性理论在砰击载荷预报领域的发展和应用研究非常必要，是该领域的重点发展方向之一。该方向的发展需要考虑计算精度的提高所造成的计算效率的下降和计算成本的上升，其造成三维时域非线性理论在工程实际应用领域进展缓慢，但相信这个问题将随着高速计算机技术的发展而逐步得到解决。

与三维时域非线性理论在船体结构砰击总体响应研究领域的应用前景类似，FEM方法、CFD方法和SPH方法作为数值仿真方法在船体结构砰击总体响应研究领域的应用也将随着高速计算机技术的发展而得到推广。不同于切片理论、三维理论、FEM方法和CFD方法，SPH方法作为一种无网格的分析流体与结构之间相互作用的方法能从另外一条途径研究砰击载荷的特性，在国内外越来越受到重视。该方法用于船舶结构砰击载荷研究的主要技术难点在于刚体和流体相互作用的边界处理问题以及砰击发生时粒子的排列被严重打乱造成的计算错误问题，但其在船舶结构砰击载荷研究领域的推广和应用是重要发展方向之一。

［1］DRUMMEN I，STORHAUG G，MOAN T.Experimen⁃tal and numerical investigation of fatigue damage due to wave-induced vibrations in a containership in head seas［J］.Journal of Marine Science and Technology，2008，13（4）：428-445.

［2］STORHAUG G.Which sea states are dimensioning for container vessels when whipping is included？［C］//Pro⁃ceeding of the ASME 2014 33rd International Confer⁃ence on Ocean，Offshore and Arctic Engineering，OMAE2014.New York：American Society of Mechani⁃cal Engineers，2014.

［3］Committee on Large Container Ship Safety.Interim re⁃port of committee on large container ship safety［R］. Tokyo：Committee on Large Container Ship Safety，2013.

［4］XING J T，SHENG Z，CUI E J.Overview of fluid structure interaction mechanics［J］.Advances in Me⁃chanics，1997，27：19-38.

［5］KORVIN-KROUKOVSKY B V，JACOBS W R.Pitch⁃ing and heaving motions of ship in regular waves，AD0134053［R］.［S.l.］：Stevens Inst of Tech Hobo⁃ken NJ Experimental Towing Tank，1957.

［6］SALVESEN N，TUCK E O，FALTINSEN O.Ship mo⁃tions and sea loads［M］.Oslo：Det Norske Veritas，1971.

［7］FALTINSEN O M，LANDRINI M，GRECO M.Slam⁃ming in marine applications［J］.Journal of EngineeringMathematics，2004，48（3/4）：187-217.

［8］BISHOP R E D，PRICE W G.The generalized anti⁃symmetric fluid forces applied to a ship in a seaway［J］.International Shipbuilding Progress，1977，24（269）：3-14.

［9］BISHOP R E D，PRICE W G.Hydroelasticity of ships［M］.London：Cambridge University Press，1979.

［10］BELIK O，BISHOP R E D，PRICE W G.On the slamming response of ships to regular head waves［J］. Transactions of the Royal Institution of Naval Archi⁃tects，1980，122：325-337.

［11］BELIK O，PRICE W G.Comparison of slamming the⁃ories in the time simulation of ship responses in irreg⁃ular waves［J］.International Shipbuilding Progress，1982，29：173-187.

［12］CLARKE J D.Wave loading in warships［C］//Advanc⁃es in Marine Structures.［S.l.］：Elsevier Applied Sci⁃ence Publishers，1986：1-25.

［13］YAMAMOTO Y，FUJINO M，FUKASAWA T，et al. Slamming and whipping of ships among rough seas in numerical analysis of the dynamics of ship structures［C］//Proceedings of Euromech Colloquium.Paris，1979.

［14］YAMAMOTO Y，SUGAI K，INOUE H，et al.Wave loads and response of ships and offshore structures from the viewpoint of hydroelasticity［C］//Advances in Marine Structures Conference.Dunfermline，Scot⁃land，1986.

［15］WU M K，MOAN T.Linear and nonlinear hydroelas⁃tic analysis of high-speed vessels［J］.Journal of Ship Research，1996，40（2）：149-163.

［16］GU M X，WU Y S，XIA J Z.Time domain analysis of non-linear hydroelastic response of ships［C］//Pro⁃ceeding of the 4th International Symposium on Practi⁃cal Design of Ships and other Floating Strucures.Var⁃na，Bulgaria，1989.

［17］SODING H.Leckstabilitate in seegang，Report 429［R］.Hamburg：Institute fur Schiffbau Hamburg，1982.

［18］XIA J，WANG Z.Time domain hydroelasticity theory of ships responding to waves［J］.Journal of Ship Re⁃search，1997，41（4）：286-300.

［19］XIA J，WANG Z，JENSEN J J.Non-linear wave loads and ship responses by a time-domain strip theo⁃ry［J］.Marine Structures，1998，11（3）：101-123.

［20］WATANABE I，UENO M，SAWADA H.Effects of bow flare shape to the wave loads of a container ship［J］.Journal of the Society of Naval Architecture of Ja⁃pan，1989，166：259-266.

［21］任慧龙.非线性波浪载荷与船体极限强度［D］.哈尔滨：哈尔滨工程大学，1995.

［22］FALTINSEN O M.The effect of hydroelasticity on ship slamming［J］.Philosophical Transactions of the Royal Society ofLondon：Series A，1997，355（1724）：575-591.

［23］PARK S W，LEE J K，OH S H，et al.Whipping anal⁃ysis of ship hulls considering slamming impact loads［C］//Proceedings of the Thirteenth International Off⁃shore and Polar Engineering Conference.Honolulu，Hawaii，USA，2003：2799-2805.

［24］GU X K，SHEN J W，MOAN T.Efficient and simpli⁃fied time domain simulation of nonlinear responses of ships in waves［J］.Journal of Ship Research，2003，47（3）：262-273.

［25］FALTINSEN O M，LANDRINI M，GRECO M.Slam⁃ming in marine applications［J］.Journal of Engineer⁃ing Mathematics，2004，48（3/4）：187-217.

［26］HERMUNDSTAD O A，MOAN T.Numerical and ex⁃perimental analysis of bow flare slamming on a Ro-Ro vessel in regular oblique waves［J］.Journal of Marine Science and Technology，2005，10（3）：105-122.

［27］EL MOCTAR O，SCHELLIN T E，PRIEBE T.CFD and FE methods to predict wave loads and ship struc⁃tural response［C］//Proceedings of the 26th Sympo⁃sium on Naval Hydrodynamics.Rome，Italy，2006：17-22.

［28］SCHELLIN T E，EL MOCTAR O.Numerical predic⁃tion of impact-related wave loads on ships［J］.Jour⁃nal of Offshore Mechanics and Arctic Engineering，2007，129（1）：39-47.

［29］OBERHAGEMANN J，HOLTMANN M，EL MOC⁃TAR O，et al.Stern slamming of a LNG carrier［J］. Journal of Offshore Mechanics and Arctic Engineer⁃ing，2009，131（3）：0310031-0310039.

［30］HERMUNDSTAD O A，MOAN T.Efficient calcula⁃tion of slamming pressures on ships in irregular seas［J］.Journal of Marine Science and Technology，2007，12（3）：160-182.

［31］ZHAO R，FALTINSEN O M，AARSNES J V.Water entry of arbitrary two-dimensional sections with and without flow separation［C］//Proceedings of the 21st Symposium of Naval Hydrodynamics.Trondheim，1996：408-423.

［32］WANG X L，HU J J，GU X K，et al.Wave loads in⁃vestigation of a VLCC by experimental and theoretical methods［C］//Proceedings of the ASME 2014 33rd In⁃ternational Conference on Ocean，Offshore and Arc⁃tic Engineering.San Francisco，California，USA，2014：V08AT06A008.

［33］WU M K，HERMUNDSTAD O A.Time-domain sim⁃ulation of wave-induced nonlinear motions and loadsand its applications in ship design［J］.Marine Struc⁃tures，2002，15（6）：561-597.

［34］O'DEA J，POWERS E，ZSELECSKY J.Experimen⁃tal determination of nonlinearities in vertical plane ship motions［C］//Proceedings of 19th Symposium on Naval Hydrodynamics.Washington D C：National Academy Press，1994.

［35］LIN W M，MEINHOLD M，SALVESEN N，et al. Large-amplitude motions and wave loads for ship de⁃sign［C］//Proceedings of 20th Symposium on Naval Hydrodynamics.Santa Barbara，US，1996.

［36］WU M K，MOAN T.Efficient calculation of wave-in⁃duced ship responses considering structural dynamic effects［J］.Applied Ocean Research，2005，27（2）：81-96.

［37］FONSECA N，GUEDES S C.Comparison of numeri⁃cal and experimental results of nonlinear wave-in⁃duced vertical ship motions and loads［J］.Journal of Marine Science and Technology，2002，6（4）：193-204.

［38］JENSEN J J，DOGLIANI M.Wave-induced ship hull vibrations in stochastic seaways［J］.Marine Struc⁃tures，1996，9（3）：353-387.

［39］STORHAUG G.Experimental investigation of wave induced vibrations increasing fatigue damage in ships［D］.Trondheim：Norwegian University of Science and Technology，2007.

［40］VIDIC-PERUNOVIC J.Springing response due to bi⁃directional wave excitation［D］.Lyngby：Technical University of Denmark，2005.

［41］FALTINSEN O.Sea loads on ships and offshore struc⁃tures［M］.Cambridge：Cambridge University Press，1990.

［42］FARNES K A.Long-term statistics of response in non-linear marine structures［D］.Trondheim：Nor⁃wegian University of Science and Technology，1990.

［43］ISSC.Report of special task committee VI.1：Extreme hull girder loading［C］//Proceedings of 14th Interna⁃tional Ship and Offshore Structures Congress.Nagasa⁃ki，Japan，2000.

［44］GUEDES S C，FONSECA N，PASCOAL R.Long term prediction of non-linear vertical bending mo⁃ments on a fast monohull［J］.Applied Ocean Re⁃search，2004，26（6）：288-297.

［45］FONSECA N，GUEDES C G.Non-linear wave in⁃duced responses of ships in irregular seas［C］//Pro⁃ceedings of 17th International Conference on Offshore Mechanics and Arctic Engineering.Lisbon，Portu⁃gal，1998.

［46］FONSECA N，GUEDES C G.Time-domain analysis of large-amplitude vertical ship motions and wave loads［J］.Journal of Ship Research，1998，42（2）：139-153.

［47］BAARHOLM G S，MOAN T.Estimation of nonlinear long-term extremes of hull girder loads in ships［J］. Marine Structures，2000，13（6）：495-516.

［48］WINTERSTEIN S R，UDE T C，CORNELL C A，et al.Environmental parameters for extreme response：Inverse form with omission factors［C］//Proceedings of 6th International Conference on Structural Safety and Reliability.Innsbruck，Austria，1993.

［49］BAARHOLM G S，MOAN T.Application of contour line method to estimate extreme ship hull loads con⁃sidering operational restrictions［J］.Journal of Ship Research，2001，45（3）：228-240.

［50］BAARHOLM G S，JENSEN J J.Influence of whip⁃ping on long-term vertical bending moment［J］.Jour⁃nal of Ship Research，2004，28（4）：261-272.

［51］WU Y S.Hydroelasticity of floating bodies［D］.Lon⁃don：Brunel University，1984.

［52］PRICE W G，WU Y S.Structural responses of a SWATH or multi-hull vessel travelling in waves［C］// International Conference on SWATH Ships and Ad⁃vanced Multi-Hulled Vessels.London：RINA，1985.

［53］WU Y S.A general interface boundary condition［R］. Wuxi：China Ship Scientific Research Center，1990.

［54］TIMMAN R，NEWMAN J N.The coupled damping coefficients of symmetric ships［J］.Journal of Ship Re⁃search，1962，5（4）：34-55.

［55］杜双兴.海洋浮体结构的直接分析方法——三维线性水弹性随机分析理论及应用［D］.无锡：中国船舶科学研究中心，1990.

［56］DU S X，WU Y S.A fast evaluation method and a dy⁃namic mode refinement method in hydroelastic analy⁃sis of marine structures［R］.Wuxi：China Ship Scien⁃tific Research Center，1993.

［57］杜双兴.完善的三维航行船体线性水弹性力学频域分析方法［D］.无锡：中国船舶科学研究中心，1996.

［58］WU Y S，MAEDA H，KINOSHITA T.The second or⁃der hydrodynamic actions on a flexible body［J］.Jour⁃nal of Institute of Industrial Science of University of Tokyo，1997，49（4）：8-19.

［59］TIAN C，WU Y S.The non-linear hydroelastic re⁃sponses of a ship travelling in waves［C］//Proceedings of Hydroelasticity in Marine Technology.UK，2006.

［60］田超.航行船舶的非线性水弹性理论与应用研究［D］.上海：上海交通大学，2007.

［61］HIRDARIS S E，PRICE W G，TEMAREL P.Twoand three-dimensional hydroelastic modeling of a bulker in regular waves［J］.Marine Structures，2003，16（8）：627-658.

［62］AKSU S，PRICE W G，TEMAREL P.A comparisonof two-dimensional and three-dimensional hydroelas⁃ticity theories including the effect of slamming［J］. Proceedings of the Institution of Mechanical Engi⁃neers：Part C Journal of Mechanical Engineering Sci⁃ence，1991，205（1）：3-15.

［63］王朝晖，夏锦祝，吴有生.弹性船体波激响应时域过程的数值模拟［J］.中国造船，1995（4）：91-96. WANG Zhaohui，XIA Jinzhu，WU Yousheng.Time domain numerical simulation of wave-induced re⁃sponses of elastic ships［J］.Shipbuilding of China，1995（4）：91-96.

［64］王大云.三维船舶水弹性力学的时域分析方法［D］.无锡：中国船舶科学研究中心，1996.

［65］WANG D Y，WU Y S.Three dimensional hydroelas⁃tic analysis in time domain with application to an elas⁃tic ship model［J］.Journal of Hydrodynamics：Ser. B，1998（4）：54-61.

［66］KASHIWAGI M.A time-domain mode-expansion method for calculating transient elastic responses of a pontoon-type VLFS［J］.Journal of Marine Science and Technology，2000，5（2）：89-100.

［67］陈徐均.浮体二阶非线性水弹性力学分析方法［D］.无锡：中国船舶科学研究中心，2001.

［68］陈徐均.超大型浮体的非线性水弹性分析［R］.上海：上海交通大学，2003.

［69］LIU X D，SAKA S.Time domain analysis on the dy⁃namic response of a flexible floating structure to waves［J］.Journal of Engineering Mechanics，2002，128（1）：48-56.

［70］DOMINIC J，PIRO A.Hydroelastic method for the analysis of global ship response due to slamming events［D］.Ann Arbor：University of Michigan，2013.

［71］BEREZNITSKI A，KAMINSKI M L.Practical impli⁃cations of hydroelasticity in ship design［C］//Proceed⁃ings of 12th International Offshore and Polar Engi⁃neering Conference（ISOPE-2002）.Kyushu，Japan，2002.

［72］袁罡.江海直达船砰击引起的鞭击振动研究［D］.武汉：武汉理工大学，2011.

［73］刘正国.江海直达船砰击弯矩研究［D］.武汉：武汉理工大学，2013.

［74］EL MOCTAR O，OBERHAGEMANN J，SCHELLIN T E.Free surface RANS method for hull girder spring⁃ing and whipping［C］//Proceedings of the SNAME Annual Meeting.Houston，TX，2011.

［75］郑兴.光滑质点流体动力学（SPH）算法研究［D］.哈尔滨：哈尔滨工程大学，2005.

［76］SUN F F.Investigations of smoothed particle hydrody⁃namics method for fluid-rigid body interactions［D］. Southampton：University of Southampton，2013.

［77］ZHAO R，FALTINSEN O，AARSNES J.Water entry of arbitrary two-dimensional sections with and with⁃out flow separation［C］//Proceedings of the 21st Sym⁃posium on Naval Hydrodynamics.Washington D C，USA，1996：408-423.

［责任编辑：易基圣］

Review of the Theoretical Investigation of Slamming of Global Wave Loads on Ship Structures

WANG Xueliang，YANG Peng，GU Xuekang，HU Jiajun
China Ship Scientific Research Center，Wuxi 214082，China

The global wave loads slammed on ship structures is a strong nonlinear problem of fluid struc⁃ture interaction.It usually results in major vibration of the hull girder according to the 2-node resonant fre⁃quency in waves，which is called whipping.Two kinds of structural problems are caused by whipping:the ultimate strength problem and the fatigue damage problem，both of which are unavoidable in the design of ship structures.In this paper，theoretical investigation of the problem presented above is reviewed systemi⁃cally，and both advantages and disadvantages of two-and three-dimensional theories in the prediction of the slamming force are presented.The review shows that certain basic assumptions and mathematical mod⁃els in the two-dimensional theory may pose restrictions on the wide application of the two-dimensional the⁃ory in hypertrophy vessels，multi-body vessels，and ocean platforms，though it has been used for more than half century.However，the three-dimensional theory bypass those restrictions and can be used more widely in naval architectures and ocean engineering.The three-dimensional hydro-elasticity theory includes some nonlinear effects such as the flare influence and can be used to predict the slamming with a higher accura⁃cy.This is one of the most important developing direction of the theoretical investigation for the slamming of global wave loads on ship structures.

ship structures；slamming；whipping；hydro-elasticity theory of ships

U661.4

A

10.3969/j.issn.1673-3185.2015.01.002

2014-06-14

网络出版时间：2015-1-28 12:04

国家部委基金资助项目

汪雪良（通信作者），男，1977年生，博士，高级工程师。研究方向：船舶与海洋结构物波浪载荷。E⁃mail：wangxl@cssrc.com.cn