水动力载荷下复合材料螺旋桨强度评估

陈　悦，朱　锡，黄　政，周振龙

水动力载荷下复合材料螺旋桨强度评估

陈悦，朱锡，黄政，周振龙

海军工程大学舰船工程系，湖北武汉430033

为开展水动力载荷下复合材料螺旋桨强度评估研究，首先采用ANSYS/CFD计算螺旋桨流体模型在设计工况下的水动力载荷，并基于ABAQUS软件通过编码INP文件将水动力载荷施加于螺旋桨结构强度模型上；然后基于Hashin失效准则，分析不同铺层角下螺旋桨可能出现的失效模式，进行复合材料螺旋桨结构强度的评估分析；最后，依据应力等效原则，将水动压力载荷等效为集中载荷，开展模型桨静强度试验和仿真计算。结果显示：仿真计算结果与试验结果吻合良好，最大误差在9%以内，验证了复合材料螺旋桨强度评估方法的可靠性。

复合材料；螺旋桨；强度评估；Hashin失效准则

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20150128.1203.013.html

期刊网址：www.ship-research.com

引用格式：陈悦，朱锡，黄政，等.水动力载荷下复合材料螺旋桨强度评估［J］.中国舰船研究，2015，10（1）：19-26. CHEN Yue，ZHU Xi，HUANG Zheng，et al.Strength evaluation of the composite propeller under hydrodynamic fluid load［J］.Chinese Journal of Ship Research，2015，10（1）：19-26.

0　引言

复合材料螺旋桨的结构强度评估是其推广应用时必须考虑的重要部分。相对于传统的金属桨，复合材料螺旋桨的强度评估存在一定的差异。在不同的纤维铺层设置下，其特有的弯扭耦合效应导致应力分布、桨叶破坏位置有所不同，且复合材料螺旋桨的破坏形式较复杂，简单地以传统螺旋桨的悬臂梁方法进行校核，以强度储备系数作为衡准是远远不够的，所以在借鉴传统螺旋桨校核方法的基础上，寻找合适的复合材料螺旋桨校核方法和衡准要求很有必要。

国内计算传统螺旋桨强度的近似方法有多种，常用的有《钢质海船入级与建造规范》（以下简称《规范》）校核法、分析计算法以及有限元计算法，不少学者对此展开了研究。张远双［1］依据《规范》对螺旋桨的要求，开发了基于AUTOCAD VAB的船舶螺旋桨参数化强度计算方法及相关程序。王玉华［2］编制了适用于大侧斜螺旋桨强度计算的有限元程序HPROAP，并对大量国内外正在使用的大侧斜螺旋桨强度进行了计算，指出安全系数K应满足如下原则：对于中侧斜螺旋桨，K＞15；对于大侧斜螺旋桨，K＞17。黄毅等［3］采用传统的悬臂梁法和有限元法对同一大侧斜螺旋桨强度进行了校核，发现校核结果不一致，最后分析指出，有限元法更适合用于大侧斜螺旋桨的强度校核。刘竹青等［4］将流体力学中的面元法与结构动力学中的有限元法相结合，对40个实桨的静强度予以了计算，给出民船螺旋桨静强度校核的安全系数在8.8～21.6之间。但以上研究均是针对传统的金属螺旋桨展开，复合材料螺旋桨特有的材料属性和失效模式与其相比存在差异，因此不能简单地以强度储备系数进行衡量。随着流固耦合技术的发展，洪毅［5-6］利用CFD/CSD流固耦合方法分析了特定纤维铺层角度下复合材料螺旋桨的流体性能。张帅等［7］采用双向流固耦合稳态算法研究了桨叶变形对螺旋桨性能的影响。孙海涛等［8］结合面元法与有限元法研究了考虑变形的复合材料螺旋桨的水动力及变形特性。以上学者的研究表明，利用有限元计算方法已经可以对复合材料螺旋桨的水动力性能及桨叶结构变形等进行预报，但针对结构强度方面的研究却很少。

国外学者Lin等［9］采用升力面理论及最小方差法光顺流体水动力载荷，采用Hashin失效准则评估了复合材料螺旋桨的桨叶强度。Jose等［10］在水弹性方法中加入Tsai-Wu强度准则，对舰船最大航速和巡航情况下的复合材料桨叶强度进行了分析。上述学者均未对复合材料螺旋桨桨叶的结构强度评估技术提出可靠的结论，也未开展结构强度试验进行佐证。考虑到Hashin失效准则的普适性，本文尝试基于粘性流理论来完成复合材料螺旋桨的水动力载荷计算，并采用Hashin失效准则开展复合材料螺旋桨的结构强度评估。

本文将首先基于RANS方程的粘性流理论，采用ANSYSWorkbench平台计算±45°铺层复合材料螺旋桨在设计工况下的水动力载荷。然后利用ABAQUS软件，通过编码INP文件，将水动力载荷施加于结构有限元模型，并基于Hashin失效准则开展复合材料螺旋桨的结构强度评估，分析不同铺层角度下螺旋桨可能出现的失效模式及位置。最后，依据应力等效原则，将水动力载荷等效为集中力，对真空吸附成型的复合材料螺旋桨模型进行静强度加载试验，以有效验证复合材料螺旋桨强度评估方法的可靠性。

1　复合材料螺旋桨的水动力载荷计算

1.1计算对象

计算对象为采用真空吸附成型的五叶右旋桨，直径0.24 m，侧斜角27°，毂径比0.280 7，如图1所示。其增强纤维为SW220高强玻璃纤维，基体材料为3201环氧树脂，纤维铺层角度为±45°。图2中：x，y，z代表全局坐标系；1，2轴为材料主轴，分别代表纤维的主方向和次方向；θ表示单层板1轴与x轴之间的夹角，由x轴逆时针转向1轴为正。

图1　复合材料螺旋桨Fig.1　Composite propeller model

图2　纤维铺层角度示意Fig.2　The ply angle of fiber

采用Solidworks三维建模软件建立复合材料螺旋桨的几何模型，如图3所示。增强纤维为二维正交平纹织物，SW220纤维，纤维布采用对称铺层，方向由表及里，铺层数为26层。单层板的工程弹性参数及强度参数如表1和表2所示。

图3　桨叶几何模型Fig.3　Geometric model of the propeller blade

表1　单层正交玻璃纤维布的工程弹性常数Tab.1Elastic engineering constants of the monolayer orthogonal glass fiber laminate

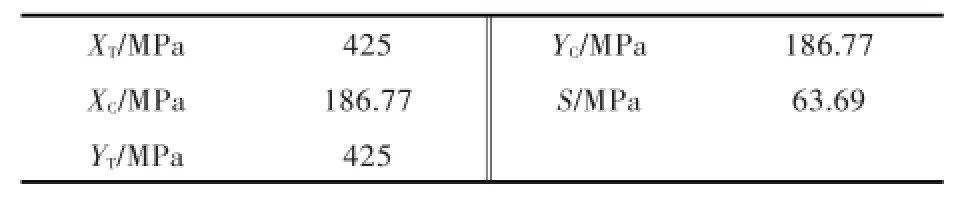
表2　单层板的强度参数Tab.2Strength parameters of the single layer

1.2流体计算

本文的流体计算基于雷诺平均（RANS）方程的粘性流理论，认为均匀来流中保持一定转速的螺旋桨周围是典型的三维不可压缩湍流流体。整个计算流场的RANS表达形式如下：

动量方程：式中：ui，uj为速度分量时均值（i，j=1，2，3）；P为压力时均值；ρ为流体密度；μ为流体粘性系数；gi为重力加速度分量为雷诺应力项。为使方程封闭，需选择合适的湍流模型进行求解，本文选择SSTk-ω湍流模型计算雷诺应力项。

流体计算域分固定域和旋转域2部分，为保证定常状态下的计算，固定域采用静止坐标系，旋转域采用单旋转系模型进行求解。采用结构化—非结构化多块混合网格划分方法划分流体网格，流场计算域网格总数约150万，如图4所示。边界条件的设定为：考虑到来流均匀，在进口边界上设定来流速度与方向；出口边界上的流动已稳定，设置为流体压力出口；螺旋桨桨叶表面定义为不可滑移壁面［11］。设定收敛判据为0.000 1，完成流体计算。

图4　流体计算域Fig.4　The fluid computational field

1.3桨叶的水动压力分布

桨叶压力面与吸力面之间的压力差，即表示该半径处桨叶所受到的水动压力载荷。图5所示在设计工况下，进速系数J=1.0，螺旋桨设计进速VA=20 kn时，目标桨桨叶各半径处压力系数CP的分布曲线，其中：Pb为螺旋桨桨叶表面受到的压力；P0为整个流体计算域的静压，为螺旋桨在指定进速下对应的来流速度。图5中，横坐标表示无量纲弦长，取值0～1代表导边至随边的分布；纵坐标表示压力系数CP。

图5　设计进速下桨叶压力值分布Fig.5　Pressure distribution prediction of the blade on designed working condition

由图5可知，在同一进速系数下，在各半径处，桨叶表面的水动压力分布呈现相似的规律：在靠近桨叶的导边及随边附近（x/c=0～0.1，x/c= 0.9～1），吸力面与压力面的压力值均出现了突变，分析其原因，认为与桨叶的大侧斜几何外形及其工作原理有关；叶面与叶背之间的压差，在叶切面弦长中部（x/c=0.1～0.8）时分布较为均匀，在x/c= 0.8处达到最大，而后至随边附近又逐渐减少，说明桨叶在导边及随边处受到的水动压力值较小。

2　复合材料螺旋桨结构强度评估算法

2.1Hashin失效准则

基于Hashin失效准则，开展复合材料螺旋桨强度评估方法分析。Hashin失效准则不仅给出了材料失效的条件，而且还给出了材料失效的模式。二维Hashin失效准则的形式如下：

1）纤维拉伸失效（σ11＞0）：

2）纤维压缩失效（σ11＜0）：

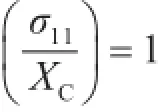
3）基体拉伸失效（σ22＞0）：

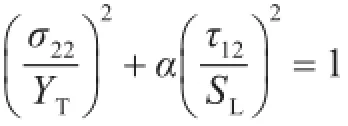
4）基体压缩失效（σ22＜0）：

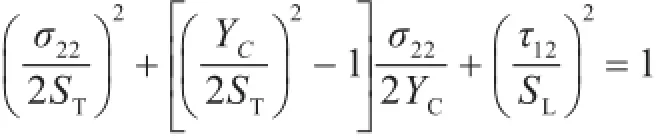
式中：σ11，σ22和τ12分别为复合材料层合板单层板的正应力与剪应力；XC，XT，YT，YC，SL，ST为复合材料层合板的6个强度参数；α为材料的非线性因子。

2.2桨叶结构强度计算

利用ABAQUS软件建立结构有限元模型，开展结构强度评估计算。通过编写相关程序，将ANSYS/CFD中的流体网格按节点进行编号，再生成对应编号的曲面，并采用六面体连续壳单元生成结构化网格，便可得到包含流体计算水动力载荷和与之相对应的结构化网格的INP文件。

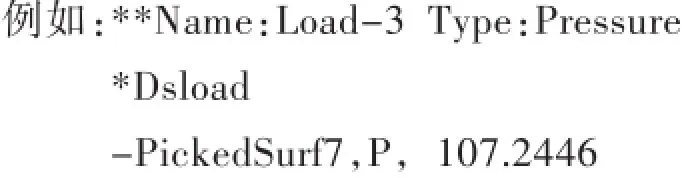
将INP文件导入ABAQUS中，实现流体水动力载荷与结构单元的对应传递，从而完成桨叶的加载［12］，如图6所示。整个桨叶共划分为280个单元，如图7所示。为便于纤维铺层计算，在桨叶厚度方向仅设置一个网格，设置纤维布铺层角度为±45°，共铺设26层；设定相关材料的属性和边界条件，采用Hashin失效准则开展复合材料螺旋桨的结构强度评估。

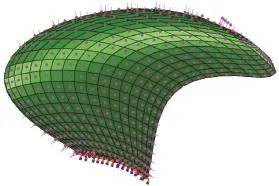
图6　水动力载荷Fig.6　The hydrodynamic load

图7　目标桨桨叶有限元模型Fig.7　Finite element model of the blade

2.3结果及分析

2.3.145°铺层复合材料螺旋桨强度评估分析

依据Hashin失效准则进行复合材料螺旋桨的结构强度评估，可以直观地判断该铺层角度下桨叶易出现的失效模式及失效位置。其中，HSNFC⁃CRT，HSNFTCRT，HSNMCCRT和HSNMTCRT分别表示纤维拉伸失效、纤维压缩失效、基体拉伸失效和基体压缩失效。对于目标桨的45°纤维铺层，由图8可以直观地看出，4种失效模式的最大Hashin失效因子分别为2.330×10-2，1.217×10-2，1.052×10-2和8.026×10-3，均小于1，由此可知在设计工况下，该复合材料螺旋桨的结构强度满足要求，且留有一定的裕度。通过4种失效模式的对比可知，45°铺层较易在r/R=0.5～0.6半径靠近随边位置处发生纤维拉伸失效，而此处的基体压缩失效因子则较小，这与桨叶的几何形状及工作原理相关。由于目标桨存在一定的侧斜，因而在r/R=0.5～0.6半径靠近随边位置处曲率较大，且此处桨叶的厚度较小，在水动力载荷的作用下，发生弯扭耦合效应后会导致桨叶出现一定的变形，从而易发生纤维拉伸失效。因此，需注意加强桨叶r/R=0.5～0.6半径随边处的桨叶强度。

图8　目标桨45°铺层失效模式比较Fig.8　Failure modes comparison of the propeller model on ply angle 45°

2.3.2-45°铺层复合材料螺旋桨强度评估分析

由图9可以直观地看出，4种失效模式的最大Hashin失效因子分别为3.985×10-2，8.614×10-3，7.922×10-3和5.347×10-3，均小于1，由此可知在水动力载荷作用下，-45°复合材料螺旋桨没有发生失效破坏，强度满足要求。通过比较可知，目标桨的-45°铺层在梢部靠近导边处易发生纤维拉伸失效：在水动力载荷作用下，导边切水会受到较大的拉伸应力，且梢部位置处的桨叶厚度较小，产生弯扭耦合效应后易发生纤维拉伸失效；而不易出现的失效模式为纤维压缩失效。

图9　目标桨-45°铺层失效模式比较Fig.9　Failure modes comparison of the propeller model on ply angle-45°

结合有限元计算的结果文件提取各层失效因子可知：4种失效模式一般首先发生于表层纤维布，如第1，2，25，26层，最后发生于中间铺层，如12～15层（表3）。因此，应重点关注桨叶表层纤维的强度以及导边和随边部位的结构强度。

表3　优先失效层的失效因子Tab.3The invalidation factors of the prior failure layer

3　复合材料螺旋桨强度试验

3.1模型桨的制作工艺

模型桨为五叶右旋桨，直径0.24 m，侧斜角27°，毂径比为0.280 7；增强纤维为SW220高强玻璃纤维，基体材料为3201环氧树脂，纤维铺层角度为±45°。考虑到模型桨的桨叶直径较小，采用RTM工艺不易控制压力，故选用真空吸附成型工艺制备复合材料螺旋桨桨叶，如图10所示。桨叶成型的主要流程包括：原材料准备、桨叶模具准备、喷涂胶衣、铺设纤维布、合模、注料成型、脱模后处理。桨毂为铝合金材料，采用五轴数控机床进行加工。桨叶与桨毂的连接形式采用螺旋插入式，以便于拆卸更换和维修，成型的模型桨如图11所示。

图10　复合材料桨叶真空吸附成型Fig.10　The vaccum adsorption modeling of composite blade

图11　复合材料螺旋桨Fig.11　The composite propeller model

3.2试验方案及实施

由于桨叶实际工作于复杂的流场中，叶面与叶背均受到流体水动力载荷的作用，且这种载荷既非常规均布载荷，也不呈现一定的函数分布，无简单规律可循，因此在目前的结构强度试验条件下，精确模拟复合材料螺旋桨桨叶所受的水动力载荷具有很大的局限性。为简化试验，并达到验证复合材料螺旋桨强度评估方法可靠性的目的，试验采用集中力静加载的形式展开。

复合材料螺旋桨的桨叶类似于悬臂梁结构，在水动压力载荷作用下，叶根处会产生较大的应力，因此依据桨叶对叶根剖面处的应力等效原则，通过有限元加载试算，将设计工况下桨叶的水动力载荷等效为集中力。

具体的测点和加载点布置如图12所示。在叶面布置6处测点：叶根的导边、中部和随边处各布置1个测点（1#，2#，3#测点），在r/R=0.6半径处的各个导边和随边处各布置1个测点（4#，6#测点），方向均沿桨叶径向；另外，为考察r/R=0.6半径处的弯曲应力，在其随边处布置1个测点（5#测点），方向沿桨叶周向。由于叶背相对于叶面其受力较小，故在桨叶叶背上仅布置3处测点，分别布置在叶根的导边和中部（7#，8#测点），以及r/R= 0.6半径处的随边（9#测点），方向均沿桨叶径向。加载点的位置为叶面r/R=0.75半径处距导边3/7位置处。

试验地点在某大学的结构与材料试验室，试验设备为电子万能试验机。加载方式为垂向加载，最大加载载荷为300 N。初始预载荷为50 N，首先，将应变仪的数据清零，然后开始加载，加载速度为0.1 kN/min。应变信号采用某大学的数据采集器进行采集。为减少复合材料制品中由气泡等缺陷引起的残余应力，试验开始时，先缓慢加载、卸载，以释放桨叶内部的残余应力。试验实施过程如图13所示。

图12　测点布置示意图Fig.12　The schematic diagram of measuring points layout

图13　试验实施过程图Fig.13　The process of experiment

3.3试验结果与有限元结果对比

为有效验证复合材料螺旋桨强度评估方法的有效性，在ABAQUS仿真计算中设置的复合材料螺旋桨的载荷大小及加载方式均与试验情况相同，以保持有限元计算结果与强度试验所测结果的一致性。图14所示为加载载荷为300 N时有限元计算的最大主应变图。图15给出了仿真计算结果与强度试验所测得各测点应变的对比，其中虚线表示试验测量的数据，实线代表仿真计算的数据。

图14　最大主应变云图Fig.14　The maximum principal strain contours

图15　各测点的试验值与有限元结果对比Fig.15　Comparison between experimental and calculated results on each measuring point

由图15（a）和图15（b）可知，仿真结果与试验结果吻合较好，各曲线的分布趋势一致，9个测点的最大误差在9%以内。从整体上看，由仿真计算所得的应变水平和试验值相比偏高，其原因主要是仿真计算中设定了叶根处为固定端，而在实际试验过程中，随着加载载荷的增加，桨叶发生了一定的弯曲变形和扭转变形，从而导致加载点的位置出现滑移，进而导致桨叶应变水平偏高。对于在桨叶叶面与叶背成对布置的测点，如1#和7#，2#和8#，以及4#和9#，其应变量也基本呈对称分布（彼此的应变量绝对值大小均在同一水平，但符号恰好相反），这表明在载荷作用下，叶面一侧均产生正应变（受拉状态），而叶背一侧则产生负应变（受压状态）。

由图15（a）可知，最大误差出现在载荷较大情况下的3#测点处，为8.2%。究其原因，是由于在载荷较大的情况下，位于叶根导边处的3#测点受到了较大的拉伸应力和弯曲应力，存在某种程度上的弯扭耦合效应，致使桨叶根部出现了微小的树脂开裂，对整个桨叶的材料属性产生了一定的影响，从而导致与有限元计算结果出现偏差；同时，因试验过程中采集数据有一定的时间差，在载荷较大的情况下就会出现应力松弛，从而使得试验测量的应变值偏小。由图15（b）可知，最大偏差出现在4#测点处，为8.85%。这主要是由于在加载力的作用下，桨叶模型产生了一定的弯曲变形和扭转变形，导致桨叶向随边方向发生了某种程度的滑移，因不能保证完全垂直加载，就使得试验结果与仿真结果出现了偏差；另外，在r/R=0.6半径的随边处，因厚度较小，加工存在一定的难度，有可能出现纤维含量不足，从而导致结果出现一定的误差。

从整体来看，试验结果与仿真计算结果趋势一致、数据吻合良好，有效验证了在等效水动力载荷作用下，复合材料螺旋桨结构强度评估方法的可靠性。

4　结论

综合以上分析，得到以下主要结论：

1）采用±45°铺层的复合材料螺旋桨，其主要失效模式为纤维拉伸失效和纤维压缩失效。应重点关注螺旋桨叶根处以及导边和随边处的结构强度。

2）45°铺层在r/R=0.5～0.6半径靠近随边位置处易出现纤维拉伸失效，-45°铺层在叶梢靠近导边部位易出现纤维拉伸失效。

3）复合材料螺旋桨静强度试验结果与有限元结果吻合良好，最大误差在9%以内，有效验证了应用Hashin失效准则进行复合材料螺旋桨强度评估的可行性与准确性。

［1］张远双.螺旋桨强度计算的参数化设计［J］.武汉船舶职业技术学院学报，2011（5）：18-20，24. ZHANG Yuanshuang.Research of propeller's strength calculation by paranmeterized method［J］.Journal of Wuhan Institute of Shipbuilding Technology，2011（5）：18-20，24.

［2］王玉华.大侧斜螺旋桨强度研究［J］.船舶力学，1998，2（2）：44-51. WANG Yuhua.Comparative studies on highly-skewed propeller strength［J］.Journal of Ship Mechanics，1998，2（2）：44-51.

［3］黄毅，许辉，姜治芳.大侧斜螺旋桨强度校核探讨［J］.中国舰船研究，2010，5（5）：44-48. HUANG Yi，XU Hui，JIANG Zhifang.Strength analy⁃sis ofhighly-skewed propeller［J］.Chinese Journal of Ship Research，2010，5（5）：44-48.

［4］刘竹青，陈奕宏，姚志崇.基于面元法及有限元法耦合的螺旋桨强度计算［J］.中国造船，2012，53（增刊1）：25-30. LIU Zhuqing，CHEN Yihong，YAO Zhichong.Statie strength analysisof civil ship propellers［J］.Shipbuild⁃ing of China，2012，53（supp 1）：25-30.

［5］洪毅.复合材料船用螺旋桨结构设计研究［D］.哈尔滨：哈尔滨工程大学，2006.

［6］洪毅.高性能复合材料螺旋桨的结构设计及水弹性优化［D］.哈尔滨：哈尔滨工程大学，2011.

［7］张帅，朱锡，侯海量.船舶螺旋桨流固耦合稳态求解算法［J］.哈尔滨工程大学学报，2012，33（5）：615-621. ZHANG Shuai，ZHU Xi，HOU Hailiang.Computation algorithm of fluid-structure interaction of marine pro⁃pellers in steady state［J］.Journal of Harbin Engineeer⁃ing University，2012，33（5）：615-621.

［8］孙海涛，熊鹰.考虑变形的螺旋桨水动力及变形特性研究［J］.哈尔滨工程大学学报，2013，34（9）：1108-1112，1118. SUN Haitao，XIONG Ying.Study on hydrodynamic and deformation performance of propellers considering the blade deformation［J］.Journal of Harbin Engineeering University，2013，34（9）：1108-1112，1118.

［9］LIN H J，LIN J J.Strength evaluation of a composite marine propeller blade［J］.Journal of Reinforced Plas⁃tics and Composites，2005，24（17）：1791-1807.

［10］JOSE P B，CHRISTIAN B，POUL A.Hydro-elastic analysis and optimization of a composite marine pro⁃peller［J］.Marine Structures，2010，23（1）：22-38.

［11］陈悦，朱锡，周振龙.考虑铺层的复合材料螺旋桨流固耦合计算及验证［J］.船海工程，2014，43（2）：57-61. CHEN Yue，ZHU Xi，ZHOU Zhenlong.Computation and confirmation of composite propeller's fluid-struc⁃ture interaction considering blade's layer［J］.Ship and Ocean Engineering，2014，43（2）：57-61.

［12］YOUNG Y L.Fluid-structure interaction analysis of flexible marine propellers［J］.Journal of Fluids and Structures，2008，24（6）：799-818.

［责任编辑：卢圣芳］

Strength Evaluation of the Composite Propeller Under Hydrodynamic Fluid Load

CHEN Yue，ZHU Xi，HUANG Zheng，ZHOU Zhenlong
Department of Naval Architecture Engineering，Naval University of Engineering，Wuhan 430033，China

The strength evaluation of composite propellers under hydrodynamic loads is studied in this pa⁃per.Firstly，the hydrodynamic load of the propeller fluid model is calculated under the designed working condition with ANSYS/CFD software.Then，the hydrodynamic load is applied on the propeller structure model through INP files with ABAQUS software.Next，the structural strength evaluation of composite pro⁃pellers is studied by analyzing the possible failure modes on different ply angles based on Hashin failure criterion.Finally，the simulation calculation and static strength test of the propeller model is carried out. During the calculation and validation tests，the hydrodynamic pressure load is regarded as equivalent to the concentration load on the basis of the stress equivalent principle.The results show that the theoretical calculation is consistent with the test and the maximum error is within 9%，which verifies the reliability of the composite propeller strength evaluation method.

composite material；propeller；strength evaluation；Hashin failure criterion

U664.33

A

10.3969/j.issn.1673-3185.2015.01.003

2014-08-20

网络出版时间：2015-1-28 12:03

国家部委基金资助项目

陈悦，女，1990年生，博士生。研究方向：船用复合材料螺旋桨。E⁃mail：chenyue322@126.com

朱锡（通信作者），男，1961年生，教授，博士生导师。研究方向：舰船结构抗爆抗冲击及装甲防护，舰船复合材料及其应用。E⁃mail：zhuxi816@163.com