严格对角占优M-矩阵最小特征值下界的改进＊

蒋建新，李艳艳*

(文山学院数学学院，云南文山663000)

下面给出一些特殊矩阵的定义与记号。

Cn×n(Rn×n)表示n × n 复(实)矩阵的集合，N = {1，2，…，n}。

集合Zn×n= {A = (aij)| A ∈Rn×n，aij≤0，∀i，j ∈N，i ≠j}中的矩阵为Z-矩阵;若A 为Z-矩阵且A-1≥0 (A-1为非负矩阵)，则A 为非奇异M-矩阵。

设A = (aij)∈Cn×n，如果i = 1，2，…，n，则称A 为行严格对角占优矩阵。

设M-矩阵A = (aij)∈Cn×n分裂为A = D -C(D = diag(a11，a22，…，ann))，称JA= D-1C 为A的迭代矩阵。

引理1［1］设A = (aij)∈Rn×n是行严格对角占优M 矩阵，

1)对于A-1= (αij)≥0 的非主对角元素满足

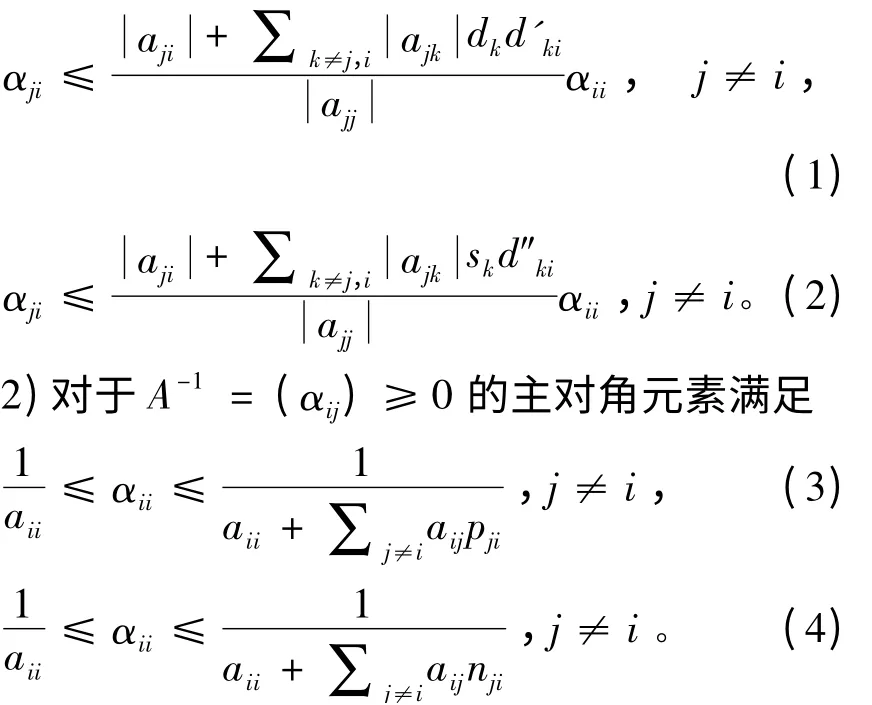
引理2 设A = (aij)∈Mn是行严格对角占优矩阵，则A-1= (αij)满足

证明 因为A 为严格对角占优M 矩阵，则A-1存在且A-1＞0(A-1的元素为正)，A·A-1= I(I 是单位矩阵)，写成分量形式，应用(1)式放缩得

同样的方法可得(6)式成立。

注释 由pji与nji的定义知它们的大小没有可比性，则(5)式与(6)式也无法比较大小。

引理3［2］设A = (aij)∈Rn×n是行严格对角占优M-矩阵，则

引理4［2］设A = (aij)∈Rn×n是行严格对角占优M-矩阵，A-1= (αij)，则

引理5［3］设M = (βij)是非奇异的M-矩阵，N =(γij)是与M 具有相同阶数的非负矩阵，N =M - A，则M-1N = JA，且满足下面的不等式

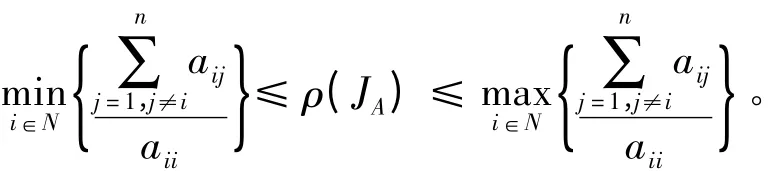
1 严格对角占优M-矩阵最小特征值的下界

这部分一方面给出严格对角占优M-矩阵最小特征值下界的几个估计式，一方面证明所得的估计式提高了文献［2］中的相应结果。

定理1 设A = (aij)∈Rn×n是行严格对角占优M-矩阵，则

证明 因为又因为JA= D-1C，C = D -A 是非负矩阵，则由引理5 知

将上述结果代入引理4 知

与定理1 同样的证明方法可得定理2。

定理2 设A = (aij)∈Rn×n是行严格对角占优M-矩阵，则

下面证明定理2，定理3 中的估计式提高了文献［2］中给出的相应结果(见本文引理3)。

定理3 设A = (aij)∈Rn×n是行严格对角占优M-矩阵，则

证明 由φi，ξi的定义知

即

定理4 设A = (aij)∈Rn×n是行严格对角占优M-矩阵，则

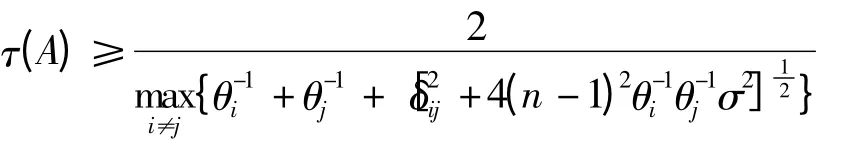
定理5 设A = (aij)∈Rn×n是行严格对角占优的M-矩阵，则

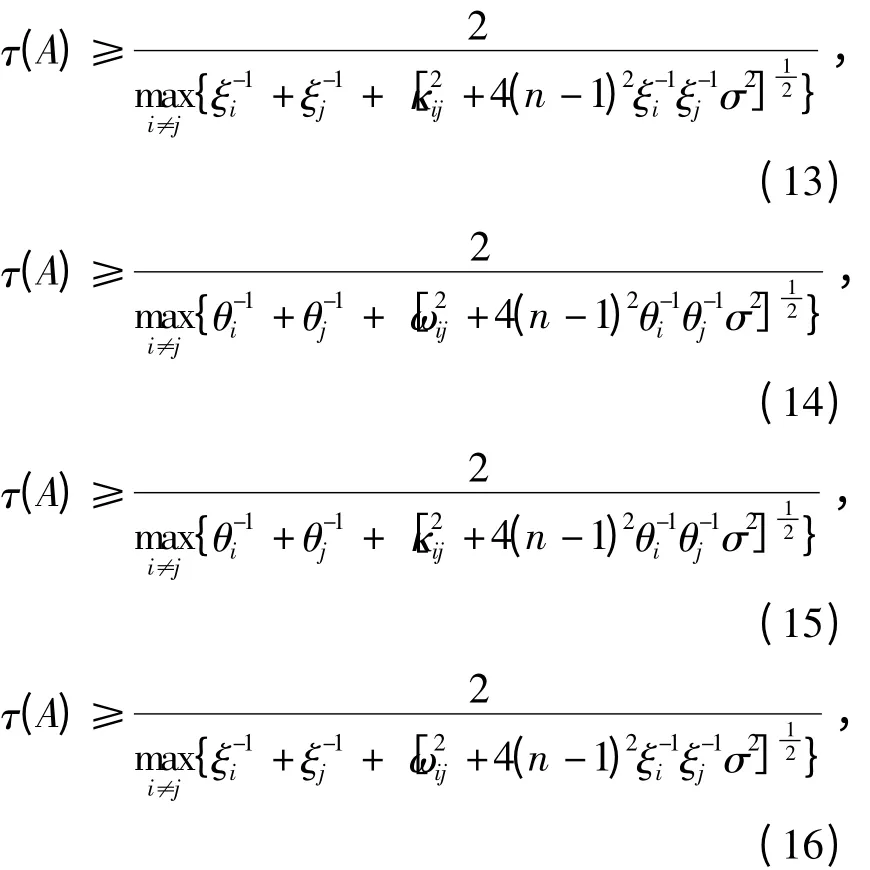
得

又因为JA= D-1C，C = D -A 是非负矩阵，则由引理5 知

同样将上述结果代入引理 4 有 τ(A)≥

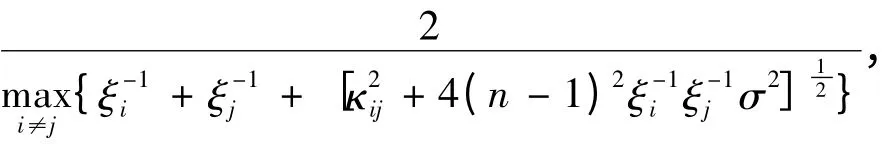
同样的方法可得式(14)～(16)成立。数值算例

设

容易验证A 是非奇异的M-矩阵，应用参考文献［2］定理4.1 知τ(A)≥0.00688007。

应用(9)，(10)，(13)～(16)式分别得:τ(A)≥0.0079，τ(A)≥0.0084，τ(A)≥0.0128，τ(A)≥0.0107 ，τ(A)≥0.0125 ，τ(A)≥0.0119。

真值为τ(A)= 1.1617 。

通过此例发现本文所得的估计式提高了引理1。

［1］李艳艳. M 矩阵特征值的新界［J］. 贵州大学学报:自然科学版，2014，31(3):8 -10.

［2］Chaoqian Li，Yaotang Li，Ruijuan Zhao. New inequalities for the minimum eigenvalue of M-matrices［J］.Linear and Multilinear Algebra，2013，61(9):1267 -1279.

［3］Tian Guixian，Huang Tingzhu. Inequalities for the minimum eigenvalue of M-matrices［J］. Electronic Journal of Linear Algebra，2010，78(20):291 -302.