整体思维：数学复习教学的有效路径

【摘 要】整体思维是一种“通体相关的思维”。用在数学教学中，则体现在问题设计的整体性、知识建构的立体性和思想方法的系统性三个方面。它利于知识左右关联、上下贯通，让“会一题，通一类，连一片”不再是口号。实践证明，整体思维符合教育学、心理学原理和学生的年龄特征，关注学习者的经验和情意，反映知识的更新过程，使数学复习教学更具有效性。

【关键词】整体思维;数学复习;课例研究

【中图分类号】G633.6 【文献标识码】A 【文章编号】1005-6009（2015）26-0036-02

【作者简介】朱桂凤，江苏省连云港市幸福路中学（江苏连云港，222023）高级教师。

2015年中考已经结束，笔者对半年来的中考复习教学进行了回顾与反思。发现在中考第一轮复习后，学生容易出现疲惫状态，数学复习教学呈现出低效现象。为克服此种情形，笔者曾上过一节基于“整体思维”的研究课（“特殊四边形”的复习教学），收到了良好的教学效果。现梳理成文，希望能给复习期的初中数学教学添就新的研究视角。

一、数学整体思维的内涵

整体思维是一种“通体相关的思维”，[1]它强调从整体上把握事物的本质，重视整体与部分的内在关联。把“整体思维”的思想方法用在数学课堂教学中，则体现为问题设计的整体性、知识建构的立体性和思想方法的系统性。整体思维利于知识左右关联、上下贯通，进而让“会一题，通一类，连一片”不再是挂在嘴边的口号;它力促一种复习行为具体化的革新，使得数学复习拥有融合度、匹配度和指向度，刷新数学复习课的旧模式，谋求数学复习教学更为有效的路径。

二、数学整体思维的实践价值

《义务教育数学课程标准》（2011年版）指出，要经历从不同角度寻求分析问题和解决问题的方法的过程，体验解决问题方法的多样性，掌握问题解决的一般方法;在运用数学表述和解决问题的过程中，体会数学的实践价值。而整体思维就体现出问题解决方法的一般化和多样性，使得数学复习教学具有“大一统”的眼界。因此，整体思维是数学复习课的精髓，能释放学生数学学习的潜力。

1.顺应学生数学认知发展水平。

初中学生的数学分析思维水平依然偏低，归结问题的能力不足，凝练方法经验的能力欠缺。这些能力的提升均离不开整体思维的参与。唯有借助整体思维，方能实现知识归位、方法到位、经验立位的立体性数学学科价值。

2.契合学生数学学习过程。

根据学生的认知规律，习得知识的过程就是将知识内化的过程。而学生在用整体思维思考问题的过程中，要经过知识的搜索和排序、思想方法的内化和提炼、基本经验的称量和借鉴等序列化思维活动。在此类思维活动的过程中，思维内层积极更新知识，使得同质知识一统、异质知识关联，实现由内而外释放知识的力量，从而建构起充满活性的知识体系。

三、数学整体思维的实践路径

整体思维是数学复习课不可或缺的思想方法。离开整体思维的指导，会压缩学生思维的兴趣，降低知识关联的融合度、弱化数理判断的匹配度、分散方法经验的指向度，使得数学复习课低效甚至无效。因此，必须高举“整体思维”的大旗，方能实现高效复习的初衷，体现学科的育人价值。

1.打通整体思维通道，凸显知识关联。

打通整体思维通道的过程，就是强化知识关联的过程。稳定的数学能力的形成需要教师的指导和学生的实践历练，就这个层面而言，唯有打通整体思维的通道、链接中考、俯瞰概念结构，方能融合知识间的内外关联，落实思维的连续性，预期繁华的思维景象。为此，笔者在复习“特殊的平行四边形”这一节内容时，首先做出如下设置。

【理论铺垫】

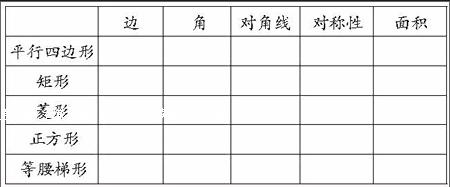
（1）特殊四边形的性质表

（2）写一个你认为合适的条件：

要使？荀ABCD成为矩形，需添加的条件是  ;要使？荀ABCD成为菱形，需添加的条件是  ;

要使矩形ABCD成为正方形，需添加  ;要使菱形ABCD成为正方形，需添加  ;

要使？荀ABCD成为正方形，需添加  ;要使梯形ABCD成为等腰梯形，需添加  。

【研究示例】

活动一：测一测

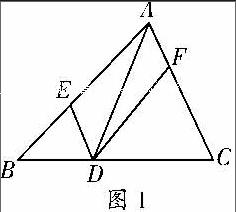
（2007年·连云港卷）如图1，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA。下列四个判断中，不正确的是（ ）。

A.四边形AEDF是平行四边形

B.如果∠BAC=90°，那么四边形AEDF是矩形

C.如果AD平分∠BAC，那么四边形AEDF是菱形

D.如果AD⊥BC且AB=AC，那么四边形AEDF是正方形

设问：若正确，说明判断依据;若不正确，更改条件使其正确。

案例中的“理论铺垫”项和“测一测”活动项，就是打通特殊四边形关联通道的具体化（站在概念识别与判断的基线上，展示概念的通性和差异）。它们使得孤立的概念群（平行四边形、矩形、菱形、正方形和等腰梯形及其元素），在直观图表的帮助下和整体思维的关联下，融合为一个不可分割的整体（特殊四边形群体的对称性）。填表的过程就是学生利用整体思维关联知识的过程（“理论铺垫”项）;判断正误的过程就是学生整体思维运行的过程（“测一测”活动项）。就教学现场来看，学生的思维活跃，兴趣思维理性化，屏蔽了思维原地踏步的低迷状态，实现了高效的数学复习。

2.和合整体思维方式，强化数理判断。

把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系，这是课标对数学教学的要求。这意味着数学复习应该更多地关注数理知识结构和完善学生的数学认知结构，重视数量关系和变化规律的符号化，强调知识与方法的匹配，形成层次分明的知识谱系。和合整体思维透过思想方法洞悉问题本质、获悉解题路径，最终实现数学复习教学的立体目标群（认知目标+动作技能目标+思维目标+情意目标）。为此，笔者设计了第二个教学活动模块。

活动二：做一做

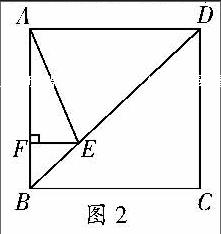
（2013年·连云港卷）如图2所示，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为  。

追问：还有其他的解法吗？

（中考指南改编题）将两张长为8、宽为2的矩形纸条交叉重叠，叠合部分面积的最小值为 ;最大值为 。

追问：画出图形并说说你的思考过程。

上述“做一做”活动就是和合整体思维的具体体现。就知识目标而言，考查对称图形的本质（等腰三角形、矩形、菱形和正方形）;就技能目标而言，考查数理能力（叠合、勾股定理的本质、角度计量）;就思维目标而言，考查转化、作差、数形结合和极限等思想方法（将图形边长转化为方程），获得最终结果的过程就是整体思维运行的过程;就情意目标而言，则使学生体会到历经思考后获得的成功感，这种成功感是由内而外的。因此，和合整体思维方式是数学复习应有的思维样态。

3.谋划整体思维主题，聚焦经验方法。

整体思维是一种设计视野，但如果没有经验方法的聚焦，则无法获取多维的思维承载体。整体思维是一种方法，但如果没有方法经验的奠基，方法只能是方法论世界的海市蜃楼;整体思维是一种理解数学的方式，但如果没有经验方法的沉淀，这种理解方式只能是句口号（思想方法隐藏在具体知识的背后）。在整体思维下注重经验方法的总结是复习教学的重头戏，因此，笔者在教学的结尾做了如下设计：

活动三：议一议

如图3，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC上，且四边形AEFD是平行四边形。

（1）AD与BC有怎样的等量关系？请说明理由;

（2）当AB=DC时，求证：？荀AEFD是矩形。

设问：你是怎样思考的？本题考查了哪些知识点和思想方法？

上述“议一议”活动，第（1）个问题是围绕概念的整体经验进行的，获取数量关系和作出判断的过程就是方法经验外显的过程;第（2）个问题是围绕意象经验的聚焦而展开的，问题分析的过程就是整体经验方法释放的过程。

综上，本案例由“理论铺垫→测一测→做一做→议一议”4个组块构成，组块1是对概念群的回溯与更新;组块2是对概念群的甄别与判断;组块3是对概念群的应用与迁移;组块4是对概念群结构的推演和升华。4个组块在适切主题的承载下有序有向地推进，它们是整体思维在数学复习教学中的具体体现，为数学复习教学的成功提供了保障。

【参考文献】

[1]蒙培元.中国哲学主体思维[M].北京：人民出版社，1993.

[2]王光明，戴永.数学命题的整体性教学策略[J].中学数学教学参考，2007（23）.