搭建学习支架,引领举一反三
茹峰
【摘要】 如何解决中考数学复习内容多、参考资料杂而课时有限的困境?本文借赏析藤丽老师《平面直角坐标系中的平行直线》一课中对一道中考复习题的支架式教学,指出中考数学复习课应该借助重点习题的教学构建一个递进式的知识体系,让学生消化得了,并形成数学思考与方法,学生举一反三。
【关键词】 中考题 数学复习 支架
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2016)02-073-030
一、背景
面对历年的中考数学难题,不少老师总是感到变化无常而无规律可循,导致复习时械重复训练很多且收效甚微。近年来,笔者听过不少复习课,但印象颇深的要数宁波蛟川书院藤丽老师的课了。藤老师借助2012年中考数学宁波卷第26题的第(3)问,以两条平行线为基本模型,由平面直角坐标系中的简单的平行线设计开放性问题让学生积极探索,充分挖掘平行线在数学中考中的广泛应用,科学地设置了知识的结合点和生长点,通过模型的不断变式,有效地启发和培养了学生的数学思维方式,使在场教师受益匪浅。
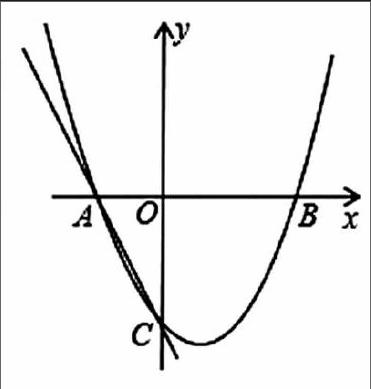
原题:如图,在平面直角坐标系中,一条抛物线经过点A(-2,0)、B(0,-1)、C(1,0)。在此抛物线上是否存在点F,使得以F为圆心、为半径的圆和直线AB相切 ?若存在,请求出所有点F的坐标;若不存在,请说明理由。
很明显,这一习题的解答对知识的综合运用程度极高,依现行的初中数学毕业班备考阶段的通行做法,本题讲解的一般思路是:考点分析——解题分析——解题过程讲解——方法总结。选择这种习题讲授法的教师占多数,主要原因是心理上所承受的中考应试压力大,理念上受“双基”的影响,行为上采取“满堂灌”式的传授。但依伍德的学习支架理论来进行教学诊断,这种常规讲解方法属于支架过度:教师代替并束缚了学生的思维,就算学生听懂了也只是达成了一个短期的记忆效果,并没有让大多数学生获得数学思想上的认知或收获。还有部分教师选择的是先学后教的方式,让学生以合作探究或独立思考方式先进行自我尝试,然后再进行全面讲解。但由于第(3)问不易想出解题方法,学生的“已知区”与“最近发展区”之间鸿沟过大,多数学生都会束手无侧。本文拟结合藤老师的教学过程作一个赏析评价,与同行分享并研讨。
二、学习支架的递进构建
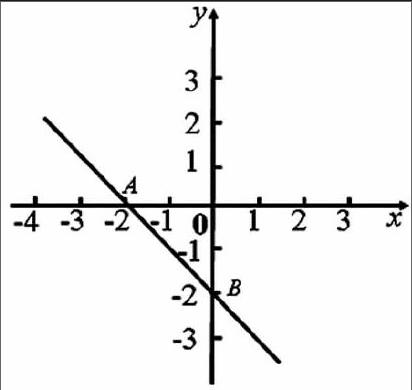
支架性问题1:如图,在平面直角坐标系中,直线AB 分别交x轴,y轴于点A(-2,0),B(0,-2)。(1)求直线AB的函数解析式;(2)若直线l与直线AB平行,增加一个怎样的条件就可以确定直线l的解析式?(3)若直线AB 向下平移2个单位,求所得的函数解析式?
分析:对于(2)的解答有学生提出增加“直线l过一个定点(0,1)”。因为通过第一小题可得直线AB的函数解析式为y=-x-2,再结合已知条件两直线平行,则x的系数是相等的,所以只要再知道一个点的坐标就可以确定函数解析式了。
有学生认为,若知道直线l与AB之间距离为22,应该可以得出函数解析式的。
有的则说可以增加“将直线AB向右平移1个单位”。还有的认为可以求出点A和点B的对应点,从而两点决定一条直线。有一个学生则认为:平移后的直线和原直线平行,所以k=-1,如增加(3),则直线l与y轴的交点为(0,-4)”函数解析式为y=-x-4。
教学评析:通过开放性问题的设问,能有效打开学生的思维,可以让学生积极探索,归纳总结两平行直线解析式的
特征和决定一直线的条件,
为下面的教学埋下了伏笔。
支架性问题2:如图,在平面直角坐标系中,直线y=-12x-1分别交x轴, y轴于点A、B. 若直线l与直线AB平行,且与直线AB的距离等于55.求直线l的解析式。
师生解析:过A作PA⊥AB,使得PA=55,再过点P作PM⊥x轴,
则△AOB∽△PAM,得到AM=15,PM=25,所以点P(-95,25),过P作直线l∥AB,设直线l为y=-12x+b代入点P得b=-12,类似地在直线AB下方也可以求出b=-32.
既然只要再求出一个点就可以确定解析式了,那么我们这个点就可以取得特殊点,在y轴上找一点P,使得PM⊥AB,则△BMP∽△BOA,得到点P(0,-12),所以直线l为y=-12x-12,类似直线下方的解析式为y=-12x-32.
教学评析:用特殊点和方程思想来解决问题,其实线段与点的坐标也存在着一定的关系,得出y=-12x-12是由原来直线向上平移12个单位,或者向下平移12个单位得到进一步强化通过平行线之间的距离来求解析式,强化用特殊到一般,熟练掌握用方程的思想在几何中的运用。
支架性问题3:如图,在平面直角坐标系中,一条抛物线经过点A(-2,0),B(0,-1),C(1,0)。问题1:在此抛物线上是否存在点D,使得以A、B、C、D为顶点、BC为腰的四边形是梯形?
若存在,请求出所有点D的坐标;若不存在,请说明理由。
师生解析:当AC为底时,过点B作BD∥AC,得点D1 (-12,-1);当AB为底时,过点C作CD∥AB,点D为直线CD与抛物线的交点,求得D2 (-3,2)。
教学评析:用分类思想探究问题,方程思想解决问题,从而求出点D坐标。这里已经逐步过渡到第26题的第3问,让学生回忆并用转化的思想。让分类更为完备,逐步加大平行线想象难度,培养学生的分类思想,同时也强化了两平行线的函数特征。
支架性问题4:如图,在平面直角坐标系中,一条抛物线经过点A(-2,0)、B(0,-1)、C(1,0)。问题2:在此抛物线上是否存在点E,使得△ABE的面积等于0.5 ?若存在,请求出所有点E的坐标;若不存在,请说明理由。
师生解析:由SΔABC=12和AB=5,可得AB边上的高为55,那么就是学生7所求的两直线和已知抛物线的交点,计算得E1(-2-1,22),E2(2-1,-22),E3(-1,-1)。
教学评析:逐步过渡到第26题的第3问,把这个问题转化为刚才我们所解的直线方程与抛物线的交点,运用了方程的思想求解,让学生回忆并用转化的思想。
支架性问题5:如图,在平面直角坐标系中,一条抛物线经过点A(-2,0)、B(0,-1)、C(1,0)。问题3:在此抛物线上是否存在点F,使得以F为圆心、55为半径的圆和直线AB相切 ?若存在,请求出所有点F的坐标;若不存在,请说明理由。
师生解析:这个问题可以转化为就是抛物线上的点到直线AB的距离为55.
三、值得借鉴之处
藤丽老师的课为我们老师怎样上一节高效的复习课指明了方向,从课堂的教学评价来看,学生显然做到了举一反三,形成了解决所有类似问题的技能。
1.巧妙整合,形成探究支架
数学学习支架是指学生在解决数学问题的过程中老师所给予的、让学生顺利地跨越“已知区”到“最近发展区”、甚至“未知区”的支持,它具有过渡性与支撑性两个特点。复习课最忌“题海战术”与“炒冷饭”,藤老师注意知识的整合,把一道复杂习题的解析过程演变为一个平行线的系列问题进行剖析。通过一个个问题的递进式解决,最终大题的解决已经水到渠成,同时又系统地复习了相关知识,形成了解题能力。
2.开放性设问,留给学生思考
藤丽老师的很多问题都没有固定答案,她将问题的多种思考方向留给学生自己去探究,这有助于学生发散性思维的培养。
3.提炼方法,引导举一反三
数学是解决现实问题的工具与方法,更是一种思维方式与思想模型。藤老师的教学设计使学生经历了数学问题发生与发展的全过程,把综合题分解为基本题,又能把基本题整合成综合题。
四、小结
在例题教学中,我们先通过设置具有开放性的学习支架来暴露问题本质要素,引发学生对虚拟的动态点线进行追踪或以动态的观点来进行图形观察,促使学生形成必要的几何直观与数学悟性;然后再利用指南支架让学生形成解题的基本活动经验,以小结的形式及时归纳经验性的认识与思想性的认识。教师在支架的构建过程中一方面要具备重新抓住一条主线整合知识的能力,让学生有耳目一新之感,通过拾级而上顺利解决问题,又能形成思想方法与举一反三的能力。
[ 参 考 文 献 ]
[1]数学课程标准研制组.全日制义务教育数学课程标准解读[M].北京:北京师范大学出版社,2002.
[2]丁尔陞.中学数学教材教法总论[M].北京:高等教育出版社,1990.