基于随机共振的微弱信号检测适应性研究

范　剑

基于随机共振的微弱信号检测适应性研究

范剑

（台州学院机械工程学院，浙江台州318000）

不是所有类型的微弱信号经随机共振系统处理后都能被有效识别，因为随机共振的信号处理方法由于系统的跃迁和非线性等因素，会使系统输出波形相对于原信号产生一定程度的畸变，势必影响对原微弱信号的识别。本文首先从随机共振动力学机理的角度逐一分析了单频正弦信号、混频信号及非周期方波等信号的随机共振系统处理过程，然后结合随机共振系统自身的输出特性分析了对于不同类型信号检测的适应性问题。研究认为，随机共振作为一种信号处理方法，其本质是属于时域的，它的“两态输出”特性使之更适合于识别各类单周期微弱信号的周期特征，而系统的跃迁特性能用于大致地展示具有“两态特征”的非周期连续微弱信号。

微弱信号检测；随机共振；检测适应性

0　引言

利用随机共振（SR）系统的双稳态及其跃迁特性，可以借助噪声使淹没在其中的微弱信号以大幅值跃迁形态的方式凸显出来，以此识别其中微弱信号的频率特征。近年来国内外学者对于随机共振理论已有大量的研究［1-8］，胡岗等利用本征函数微扰展开方法进一步发展了随机共振理论［9-10］并进行了一系列随机共振的模拟实验［11-12］；在微弱信号检测方面，冷永刚等提出了参数调节随机共振［13］、变尺度和二次采样随机共振［14］以及级联双稳随机共振［15］等检测方法，胡茑庆等在研究随机共振原理的基础上实施了对微弱信号检测的应用［16］，本文作者所在的研究团队对其他类型的随机共振系统也做了有益探索［17-18］并进行了自适应随机共振微弱信号检测的应用研究［19］。上述研究为基于随机共振的强噪声背景下微弱信号检测应用提供了理论和实验依据。

但同时我们也注意到，已有随机共振的理论研究都是以单频正弦信号为研究对象的，而在已有基于随机共振的微弱信号检测仿真或实验研究中所提到的信号检测对象也大多是单频正弦信号或方波信号［15，20-21］。然而，这个检测方法能否适用于其它类型信号的检测呢？由于随机共振系统的非线性及其非自治性，目前还无法获得该系统输出的解析解，这也导致我们难以从数学的角度分析随机共振信号检测适应性的问题。不过随着我们对随机共振非线性动力学机理研究［22］的进一步深入，可以尝试从新的角度去分析这类问题。本文首先对比分析了随机共振系统对单频正弦信号、混频信号及非周期方波等信号的处理过程，然后结合随机共振系统自身的信号处理特性进一步分析了随机共振系统的微弱信号检测适应性。研究随机共振的微弱信号检测适应性，可以更好地明确该检测手段的适用范围，有利于充分发掘该检测方法的潜力，对基于随机共振的微弱信号检测工程应用具有重要的实际意义。

1　不同类型信号的随机共振处理过程分析

随机共振技术之所以常被用来提取淹没在强噪声环境下微弱信号的频率特征，无疑是希望系统能输出与微弱信号保持一致的同频跃迁信号，所以系统的输出首先要能发生“跃迁”，然后还要“同频”。然而相对强噪声而言，有用信号毕竟是微弱的，所以要积极调动系统内部和外部一切有利因素促成系统输出的“跃迁”，我们在文献［22］的研究中已经明确：在激励信号周期足够长的前提下，随机共振系统存在两种跃迁行为：如果内秉信号（即微弱信号）的幅值大于跃迁阈值，则系统以发生“自然跃迁”为主；反之，如果内秉信号的幅值小于跃迁阈值，则只可能在噪声的诱发作用下发生跃迁；作用于随机共振系统的内秉信号能推动系统动点沿吸引子曲线移动，它对系统的输出起内在的和本质的作用，而噪声在一定条件下能够诱发系统产生跃迁行为。那么剩下的问题是：系统输出的跃迁信号能否与原微弱信号保持“同频”。然而，经随机共振系统处理后的输出信号由于跃迁和非线性的作用已经发生了波形的畸变，它还能否有效地保持“同频”呢？这个问题需进一步分析。考虑到本文是针对随机共振系统发生跃迁后的输出信号进行分析，此处为了使问题的描述更为直观，我们直接使用内秉信号来驱动随机共振系统发生自然跃迁，而不采用噪声诱发跃迁的形式，故在后文的讨论中如无特别声明，均略去系统噪声的作用。接下来，我们有必要简要阐述随机共振非线性动力学机理，然后从这个角度去分析不同类型信号的随机共振处理过程。

取如式（1）所示的Duffing方程：

式中：k为阻尼系数，a、b分别为线性和非线性项系数，c为作用于系统的激励值，它一般由微弱信号和噪声组成。通过文献［22］的研究，我们可以得到式（1）的吸引子曲线，如图1所示。

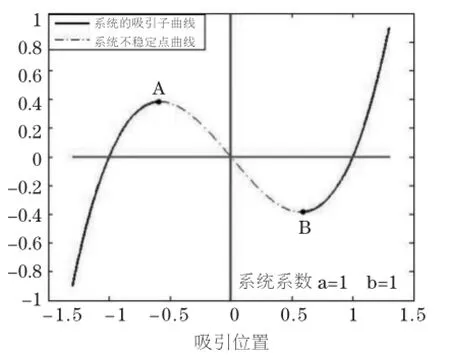
图1　SR系统的吸引子曲线Fig.1 Attractor curve of SR system

该曲线上各点的纵坐标表示作用于系统的激励值c（t），横坐标表示对应于该激励作用下系统动点的位置（亦即系统方程x的值）。通过该曲线上的激励-位置映射关系，我们可以根据系统当前的激励值获知系统方程的x值。曲线上两个极值点A、B为跃迁点，其纵坐标值为。系统动点位置的变化由激励信号驱动，并始终沿着该吸引子曲线移动，当激励值往上越过A点或往下越过B点时，系统的输出便会发生从左向右或从右向左的跃迁。

1.1随机共振系统对单频正弦信号的处理

构建参数为k=0.1，a=1，b=1的随机共振系统，取一单频正弦激励信号，考虑到该信号的周期应足够长，此处取其频率为0.1Hz，并取能够发生自然跃迁的激励信号幅值为0.5（大于该系统跃迁阈值的绝对值0.385）。把该单频正弦信号作为系统的激励输入系统，其输入和输出波形如图2所示。图中的两条水平虚线为跃迁阈值线，激励信号（图中表示为点划线）的上升沿与它有相交，如图中P点所示，也就意味着随着激励值继续上升，它将大于跃迁阈值，必然导致系统输出发生跃迁，如图2中的实线曲线CD段所示；随着激励信号增加到正的最大值然后又逐渐减小，并朝负值方向变化，当激励值变化至图中的Q点以下时，它又将引起系统动点反方向的跃迁，如图中输出波形曲线的EF段所示。我们把这一过程置于吸引子曲线图中去理解，将会变得更为直观，如图3所示，随着激励值超越A点，系统发生从C到D段的跃迁，同理，当激励值减小到B点以下时，系统输出发生从E到F段的跃迁。在这两个图中都可以看出，由于激励幅值的对称性，在正半周期的激励会超越正的跃迁阈值，从而发生从左向右的跃迁，负半周期激励值同样也会超越负的跃迁阈值，于是动点就发生从右向左的跃迁，然后又如此周而复始，使得跃迁的过程也表现出与原信号一致的周期性。然而由于在随机共振处理过程中存在吸引子曲线映射的非线性及跃迁等因素，其输出波形与原信号波形有很大程度的畸变，通过Fourier变换可以看到频谱图上有一系列幅值逐渐衰减的倍频信号，如图4所示，有的文献将这一特点用于辅助判断微弱信号的频率成分［23］。

图2　单频正弦信号及其SR输出信号波形Fig.2 Single sinusoidal input signal and its output signal of the SR system

不过须要指出的是，随机共振的微弱信号检测过程是在调节系统参数、观察系统输出的过程中做逐步对比来甄别的，此处我们通过调节参数a、b的值来改变跃迁阈值，也就是改变图2中水平虚线的高度位置，从图中可以发现，只要信号的幅值大于系统的跃迁阈值，那么，根据前述分析可知，系统的输出必然会呈现周期性的往复跃迁，且能与原信号较好地保持同频。所以，随机共振的检测方法对于单周期正弦信号而言，是具有较好检测适应性的。

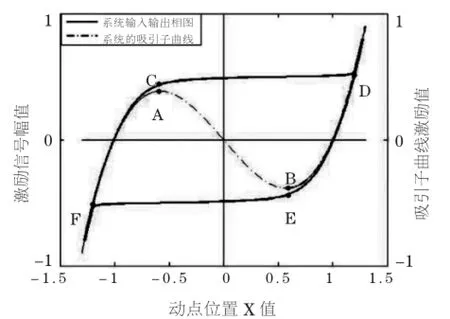
图3　随机共振系统的相图Fig.3 The phase portrait of the SR system

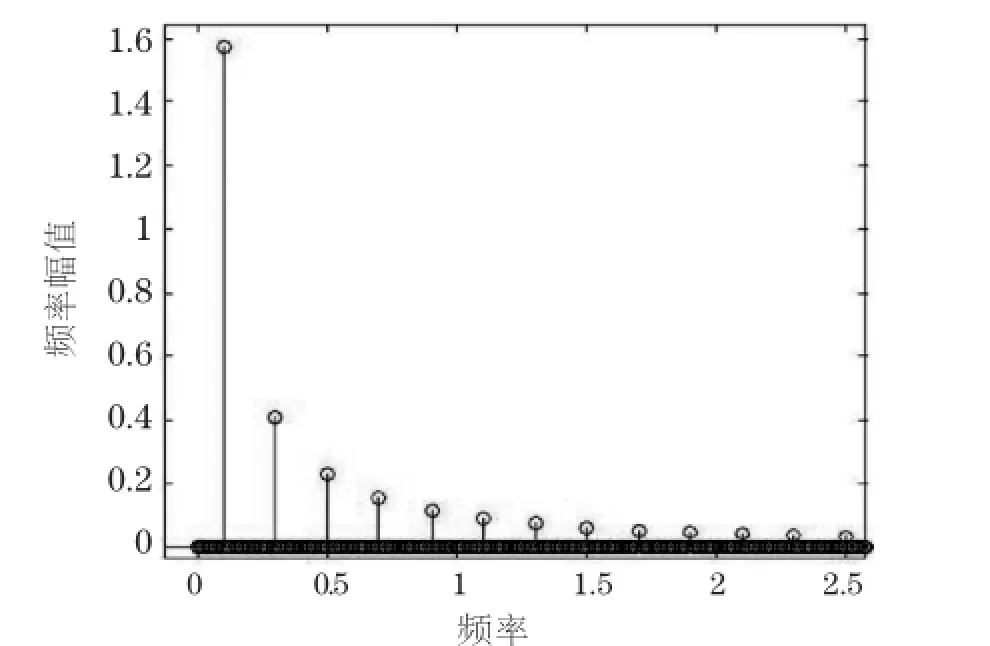
图4　单周期信号经随机共振系统处理后的输出信号频谱Fig.4 Output signal spec trum of the SR system for single sinusoidal input signal

1.2随机共振系统对混频信号的处理

我们再随机地取幅值、频率和初相位都不相同的两个正弦信号：S1=0.2sin（0.2t）以及S2=0.6sin（0.3t+ 0.6π），将其混合后输入由参数为k=0.1，a=0.5，b=0.5构建的随机共振系统中，系统的输入信号、输出信号波形及其频谱如图5所示。由图5a可见，在混频信号波形的正的激励值上升段以及负的激励值下降段与跃迁阈值线相交处，对应位置的系统输出都有跃迁发生，在频谱图5b上也有比较明显的一个主峰值以及其余的一些倍频信号的幅值，该频谱主峰值对应的信号频率为0.3Hz，另一个次高的频率对应为0.2Hz，但后者的幅值并不能显著地区别于其它倍频信号的幅值，而且这些倍频信号幅值也不能说明是哪个原信号频率的倍频。可见仅凭这些信息并不能直接有效地甄别出原信号的频率成分。那么我们继续调整系统参数，根据图5可以预见，如果减小系统的阈值，其输出波形的跃迁规律与当前的状态基本一致，所以系统输出信号的频谱不会有明显变化。我们逐渐把跃迁阈值增大，比如取系统参数为k=0.1，a=1.8，b=1.8，将上述混频信号加入到该系统中，可获得经随机共振系统处理后的输出波形及其频谱如图6所示。这时的系统输出信号波形与原信号相比较发生了严重畸变，而且从频谱图上也未能发现在输入和输出信号之间有直接对应关系的频率信息。所以，对于类似这样的混频信号，我们认为随机共振系统的检测能力有限。

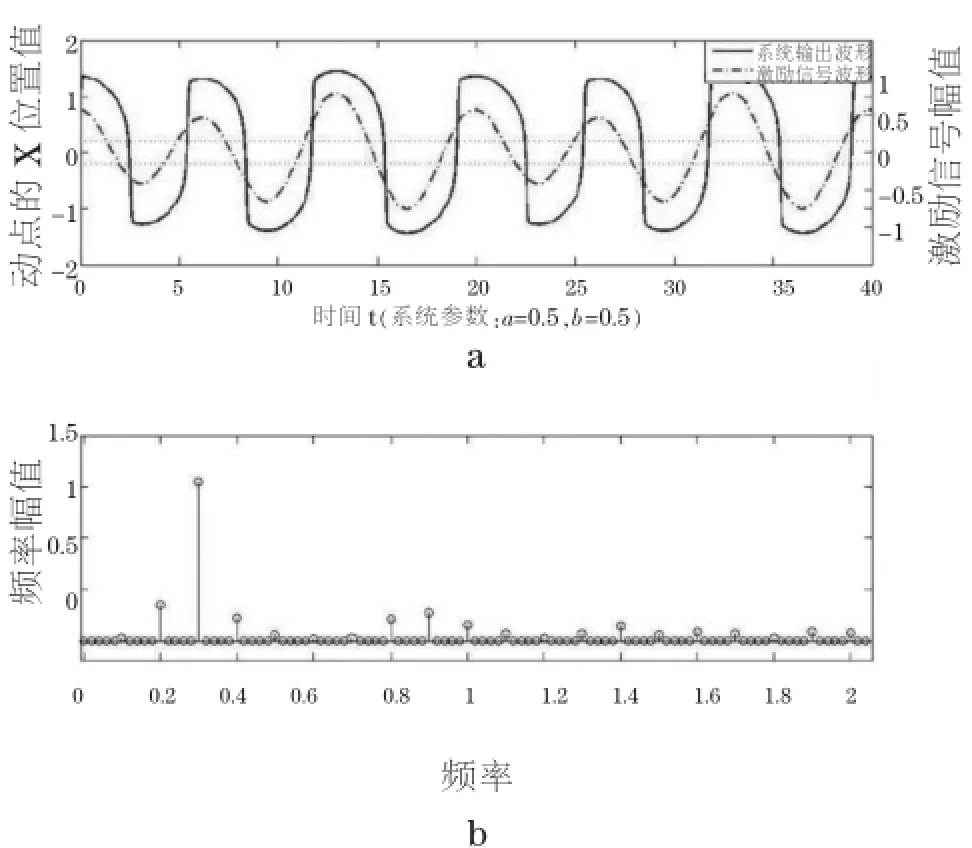
图5　混频信号及其经随机共振系统处理后的输出信号频谱Fig.5 Mixing signal and its output signal spectrum of the SR system

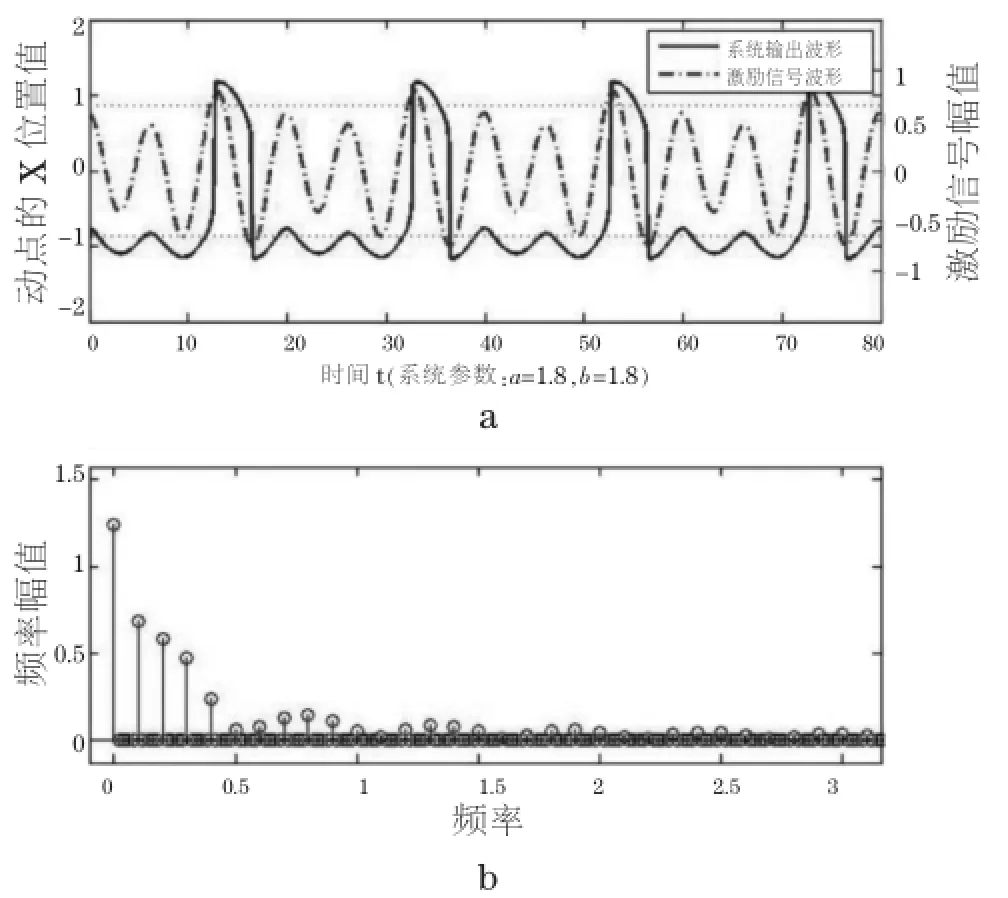
图6　阈值调整后的系统的输出信号波形及其频谱Fig.6 Input and output signal of the threshold adjusted SR system

1.3随机共振系统对非周期方波信号的处理

同样地，先构建参数为k=0.1，a=1，b=1的随机共振系统，再取如图7a图中黑色实线所示的输入信号，其中有连续的方波及间歇阵发性方波，这些方波的幅值为0.5，将该信号输入到随机共振系统可得到系统的输出如图7b图蓝色实线所示。由图可以看出，输出信号基本分居于零线的上下两侧，而且尤其值得注意的是，在间歇阵发性方波中幅值为零的各信号段所对应的输出有所不同，原因就在于其前置的信号使得系统输出发生了跃迁，有的是正向跃迁，有的是反向跃迁，这一点我们在图1所示的吸引子曲线图中可以看到，幅值为0的激励信号对应有两个吸引子位置，当前系统的动点处于哪个吸引子位置完全取决于其前置邻接的那个跃迁状态，又由于在同侧吸引子曲线上，方波幅值对应的吸引子位置与零激励的吸引子位置有一段距离，所以反映在输出波形的高度方向上有“一小段落差”。

图7　方波信号及经随机共振系统处理后的输出波形图Fig.7 Rec tangu lar Input signal and its output signal of the SR system

由这个实例的分析可以发现，随机共振系统对于方波信号的甄别能力也是有限的，它不能够有效地区别出原信号是连续方波还是间歇阵发性的方波，因为在考虑噪声的作用后，图7b中所示的那“一小段落差”将会被震荡波形取代。现举例示之：此处我们为了利用噪声的诱发跃迁作用，将原方波信号幅值调整为0.1（小于系统的跃迁阈值），然后在该信号中加入强度为0.5的高斯白噪声，把该混合后的信号输入到参数为k=0.2，a=1，b=1所构建的随机共振系统（此处把阻尼调整为k=0.2的目的，是为了有效滤除一部分噪声，同时又保证系统能在噪声的诱发作用下发生跃迁），其输入及输出波形如图8所示。有文献［23］指出可利用随机共振系统来恢复含噪方波信号，但我们通过此例可以看出，该方法适合于连续方波，而不适合于对间歇阵发性方波信号的恢复。

图8　加噪声后的方波信号及经随机共振系统处理后的输出波形图Fig.8 Noised rec tangular Input signal and its output signal of the SR system

2　随机共振系统自身特性对微弱信号检测的适应性

首先，根据输入信号与随机共振系统吸引子曲线的映射关系，可以定性地获得系统的输出信号。由于输入信号的波形是时域的，于是经吸引子曲线映射而获得的输出波形也是时域的。所以，随机共振系统作为一种信号处理方法，它在本质上是属于时域的。另一方面，由于随机共振系统的非线性及非自治性，我们还无法获得随机共振系统在时域与频域之间的变换关系，所以还不能从理论分析的角度去考察该信号处理过程在频域的表现形式。而且，从1.2节所展示的实例我们也未能在输入信号的频谱与系统输出的频谱中发现这两者之间存在明显和有效的对应关系；其次，随机共振系统的跃迁阈值是由系统参数决定的，不同的跃迁阈值会使系统输出的跃迁位置发生变化，从而使得输出波形也将发生变化，有时甚至是剧烈变化，所以不能仅凭随机共振系统的输出波形去推断、甄别原信号波形或者频率成分；再次，在吸引子曲线上无论是发生跃迁还是映射，它对原信号的处理都是非线性的，必然使得系统输出波形发生较大幅度的畸变，故而我们只能对畸变后的输出信号做一些定性的分析和判断。

但是，随机共振系统具有鲜明的“对称两态性”：吸引子曲线在左右两侧各只有一段，所以系统的输出“非左即右”，也就是说系统动点如果不出现在左侧吸引子曲线段上，就一定在右侧的吸引子曲线段上，而且这两段吸引子曲线都是从两个跃迁阈值点向两外侧延伸。于是，小幅值微弱信号经随机共振系统处理后能以大幅值跃迁的形式表现来。而且，如果原信号是单周期的，那么其跃迁周期也能较好地表现为单周期，从而能够呈现“同频”状态。所以随机共振系统适合于处理和识别各类单周期的、波形呈对称形态的微弱信号的周期特性，比如单周期正弦信号、单周期三角波、方波等信号；此外，利用随机共振系统还可以大致地展示具有“两态特征”的连续微弱信号，比如连续的周期或非周期方波等信号。

3　结语

随机共振的信号处理方法突出的优势在于它能以“大幅值跃迁”的形式呈现淹没在噪声中的微弱信号，但不是所有类型的微弱信号经随机共振系统的处理后都能被有效识别；它在本质上是属于时域的，不能简单地从频域的角度去考察该信号处理方法的性质和过程；然而其鲜明的“对称两态”输出特性使它能更有利地去识别各类单周期的、呈对称形态微弱信号的周期特征，系统的跃迁特性可用来大致地展示具有“两态特征”的连续微弱信号。

［1］R Benzi，A Sutera，A VulPiani.The m echanism of stochastic resonance［J］.J.Phys.A，1981，14（11）:453-457.

［2］Benzi，G Parisi，A Sutera，A VulPiani.Stochastic resonance in climatie change［J］.Tellus，1982，34（1）:10-16.

［3］S Fauve，F Heslot.Stochastic resonance in a bistable system ［J］.Phys.Rev.Lett.，1983，97A（1-2）:5-7.

［4］Nicolis C.Stochastic aspects of climatic transitions-additive fluctuations［J］.Tellus，1981，33（3）:225-234.

［5］F.Combet， L.Gelman.Optimal filtering of gear signals for early dam age detection based on the spectral kurtosis［J］.M echanical System s and Signal Processing，2009，23（03）:652-668.

［6］Mitaim S，Kosko B.Adaptive Stochastic resonance［J］.Proc of the 1998 IEEE，1998，86（11）:2152-2183.

［7］Jung P，H？nggi P.Stochastic nonlinear dynam ic m odulated by ex ternal periodic forces［J］.Europhy.Lett. 1989，8（6）:505-510.

［8］Masolivers J.Robinson A Coheren t stochastic resonance［J］.Phys.Rev.E，1995，51（5）:4021-4026.

［9］G，Hu.Periodically forced Fokker-Planck equation and stochastic resonance［J］.Physical review.A，1990，42（6）:2030-2041.

［10］H.Gang.Stochastic resonance in a nonlinear system driven by an aperiodic force［J］.Physical review.A，1992，46（24）：3250-3254.

［11］Hu G.，Nicolis G.，Nico lis C.，Period ically forced fokker-p lanck equation and Stochastic Resonance［J］. Phys.Rev.A，1990，42（4）:2030-2041.

［12］秦光戎，龚德纯，胡岗，等 .随机共振的模拟实验［J］.物理学报，1992，41（3）:369.

［13］Leng Yong-Gang，Wang Tai-Yong，Guo Yan et al.Study o f the property of the parameters of bistable stochastic resonance［J］.Acta Phys.Sin.，2007，56（1）:30-35.

［14］Leng Yong-Gang.Mechanism of parameter-adjusted stochastic resonance based on Kramers rate［J］.Acta Phys.Sin.，2009，58（8）:5196-5200.

［15］赖志慧，冷永刚，范胜波.级联双稳Duffing系统的随机共振研究［J］.物理学报，2013，62（7）:070503.

［16］胡茑庆，温熙森，陈敏.随机共振原理在强噪声背景信号检测中的应用［J］.国防科技大学学报，2001，23（4）:40-44.

［17］赵文礼，刘进，殷园平.基于随机共振原理的中低频信号检测方法与电路设计［J］.仪器仪表学报，2011，32（4）:721-728.

［18］赵文礼，郭丽红.随机共振及其微弱信号的自适应检测［J］.电子测量与仪器学报，2006，20（5）:21-25.

［19］王林泽，张亮，赵文礼.一种新的随机共振模型的电路设计与信号检测实验研究［J］.电路与系统学报，2013，18（2）: 482-487.

［20］Lin Min，Huang Yong-Mei.Modulation and demodu lation for detecting weak periodic signal of stochastic resonance［J］.Acta Phys.Sin.，2006，55（7）:3277-3282.

［21］Zhu Guang-Qi，Ding Ke，Zhang Yu et al.Experimental research of weak signal detection based on the stochastic resonance of non linear system ［J］.Acta Phys.Sin.，2010，59（5）:3001-3006.

［22］范剑，赵文礼，张明路，等.随机共振动力学机理及其微弱信号检测方法的研究［J］.物理学报，2014，63（11）: 110506.

［23］Zhang Zheng-w ei， Fan Yang-Yu， Zeng Li.A nonlinear hybrid m ethod fo r detec ting the frequency of unknow n w eak com posite periodic signal［J］.Acta Phys.Sin.，2006，55（10）:5115-5121.

（责任编辑：耿继祥）

Reseach on the Adaptability of W eak Signal Detection by M eans of Stochastic Resonance

FAN Jian
（School of Mechanical Engineering，Taizhou University，Taizhou 318000，China）

The method of stochastic resonance（SR）is often used to pick out the w eak signal submerged in noisy background.But the output signal of SR system can be severely distorted relative to the input，w hich can cause some difficulty in signal recognition.The SR procession of three types of signal such as single sinusoidal signal，m ixing signal and square wave are analyzed at first in this paper，and then the detection adaptability is studied according to the output property of SR system.Analysis of the result indicates that SR，as a signal processing method，belongs to time domain，and its tw o-state-output property means this processing method is especially suitable fo r recognizing singly periodic signal.Furthermore，the transition property of SR system can be app lied to recover the tw o-state aperiodic signal masked by heavy noise.

weak signal detection；stochastic resonance；detection adaptability

10.13853/j.cnki.issn.1672-3708.2015.03.007

2015-01-19

国家自然科学基金（批准号：50875070），浙江省教育厅科研项目（批准号：Y201326915）。

范剑（1977-），男，江西丰城人，博士，主要研究方向为机械系统故障诊断、微弱信号检测等。