基于频率配置和解耦率的某客车悬置系统优化设计

李智强

基于频率配置和解耦率的某客车悬置系统优化设计

李智强

（厦门金龙联合汽车工业有限公司，福建厦门361023）

建立某款中型客车动力总成悬置系统6自由度模型；以系统固有频率的合理配置和解耦率为目标函数建立悬置系统的优化设计模型，并对悬置系统进行优化设计；通过对动力总成施加发动机激振力的振动响应结果对比，表明对该悬置系统的优化有效、可行。

悬置系统；固有频率；解耦率；优化设计

悬置系统是汽车动力总成和车架（或车身）连接的桥梁，传递两者之间的相互作用力。而发动机作为汽车振动的主要来源之一，设计具有良好隔振性能的悬置系统，有效地减少发动机振动向车身的传递是提高整车NVH性能的重要课题。合理地配置悬置系统固有频率和提高各阶主振动方向的解耦率在悬置系统隔振设计中得到广泛使用，而如何更好地达到上述效果方法各异。本文建立以解耦率最大化和各阶频率逼近期望值的多目标优化模型，对某款中型客车悬置系统进行优化；并通过对动力总成施加发动机激振力，对优化前后悬置元件的动态响应传递力进行分析。

1　悬置系统的固有频率和能量解耦率

对于橡胶悬置元件，可以简化为一个具有弹性中心和3根互相垂直的弹性主轴的粘弹性构件［1］。因发动机缸体和车架的固有频率要远远大于橡胶元件，所以将其假设为刚体［2］。动力总成悬置系统简化为一个具有6自由度的力学系统，如图1所示，图中1-4分别表示四点悬置。为了二维图示清晰，仅将1、3两点的悬置元件用模型表示出来。

以动力总成质心为原点建立坐标系O-XYZ，其中X轴平行于曲轴指向发动机曲轴皮带轮侧；Z轴平行于气缸中心，向上为正；Y轴根据右手定则确定。定义动力总成的广义坐标为沿着坐标系X、Y、Z轴平动的x、y、z和绕X、Y、Z转动的θx、θy、θz，即：x=［x y z θxθyθz］。根据拉格朗日方程［3］：式中：x为系统的广义坐标；ET为系统动能；EV为系统势能；ED为系统耗散能；F为系统所受广义力。得到悬置系统6自由度振动微分方程：式中：x为系统广义坐标；M为系统质量矩阵；K为系统刚度矩阵；C为系统阻尼矩阵；F为系统广义力矩阵。

根据式（2），不考虑系统阻尼得到固有特性方程式：

根据振动理论，可求得系统的圆频率ωi为矩阵M-1K的特征值，从而得到系统固有频率：

从能量角度来说，耦合就是沿着某个广义坐标方向的力（力矩）所作的功，转化为系统沿多个广义坐标的动能和势能［4］。系统沿某个广义坐标振动的动能和势能可以互相转换，但其总和不变。当系统第i阶模态振动时，第k个广义坐标系所占的能量百分比为

2　悬置系统优化设计建模

2.1设计变量

悬置系统的隔振性能与动力总成的惯性参数、悬置元件的动刚度特性以及悬置的安装位置和角度有关系。汽车动力总成配置确定后，其惯性参数也确定，故不作为设计变量。作为客车悬置系统，为了提高设计效率、节省成本，先考虑已有的橡胶悬置元件，对悬置原件的安装位置和角度进行优化调整。若效果不佳，再考虑重新设计悬置软垫。因此，设计变量取4个悬置元件的安装位置。

2.2目标函数

系统固有频率的合理配置和提高解耦率是悬置系统隔振性能评判的重要依据，如何快速有效地达到这一设计效果有不同的方法。对于频率配置和解耦率，频率的配置应该作为主要的关注对象，在此基础上力求达到最大的解耦率。为此，本文建立以各阶频率逼近设定的期望值和解耦率最大化为目标的多目标数学模型。

悬置系统各阶振动的频率对于某个车型有其特定的设计范围。为了让系统的固有频率有更好的分布，根据这个范围为各阶频率设定一个期望值，在优化过程中让系统尽可能地逼近设定的期望值。频率部分子目标函数J1（x）如下：

式中：i为系统固有频率阶数；ω1i为第i阶固有频率的加权因子；fi（x）为第i阶系统固有频率；fsi为设定的第i阶期望频率；x为设计变量。

解耦率的计算采用能量解耦法，用EPi表示第i阶模态主振动方向所占的能量百分比。EPi越大，该方向的振动解耦度越高。系统能量解耦的子目标函数J2（x）可表示为

同时采用固有频率逼近期望值和各阶主振型方向能量解耦率最大化作为目标函数是一个多目标优化问题。在进行计算时，将多目标优化问题转换为单目标优化问题［5］。两个目标函数具有同样的数量级，可将各子目标函数加权求和得到一个新的目标函数J（x）：

式中：ω1和ω2分别为第一个目标函数和第二个目标函数的加权因子。

2.3约束条件

根据隔振理论［6］，要使悬置系统具有隔振效果，即振动的传递率要小于1，系统的固有频率要小于激励频率的1/21/2倍。发动机怠速转速为750 r/min，悬置系统频率必须低于17.68 Hz，考虑路面的激励频率，系统频率的范围设定在4.5 Hz～15 Hz。除此之外，悬置系统的频率还要避开汽车其它子系统的频率。虽然目标函数（8）使得优化过程中各阶振动频率会逼近设定的期望频率，但是仍不能保证各阶频率不会出现在不理想的区域。因此，还要对频率加以约束。另外，为了保证悬置元件的使用寿命，橡胶不能太软，悬置元件的垂向变形小于5 mm，侧向变形小于2 mm。最后，对设计变量进行约束，设计变量的范围主要根据悬置点安装位置的可变空间确定。

3　悬置系统优化实例

3.1初始状况

以某款8 m中型客车为例，该车动力总成由玉柴4缸发动机和綦江6档变速器组成。发动机后置，纵向布置。动力总成惯性参数如下：m=861 kg，Ixx=45.13 kg·m2，Iyy=176.68 kg·m2，Izz=159.96 kg·m2，Ixy=-1.76 kg·m2，Iyz= -0.04 kg·m2，Izx=31.14 kg·m2。在动力总成质心坐标系下，悬置元件优化前的位置如表1所示，前后悬置都采用V形45°角布置。前悬置左右两侧和后悬置左右两侧分别采用相同的橡胶悬置元件，其刚度参数见表2。

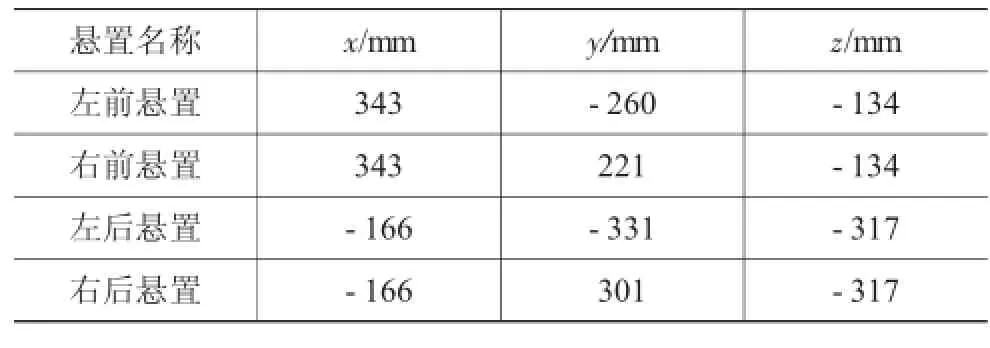
表1　优化前悬置元件坐标

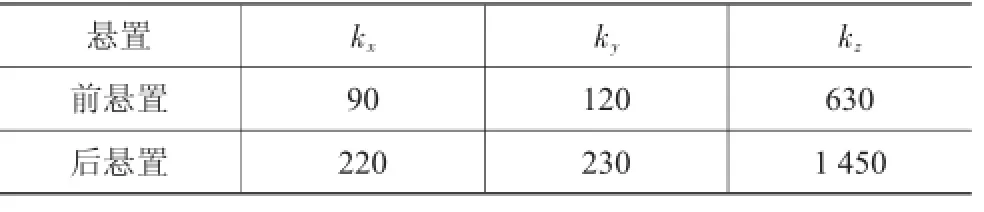
表2　悬置元件的静刚度参数N/mm

据前所述方程，编写Matlab程序，计算得到优化前悬置系统的固有频率和能量分布，见表3。各阶主振型方向的解耦率为表3中黑体所示。从计算结果可知，悬置系统X方向的固有频率偏低，容易影响悬置元件的寿命；从解耦率方面看，X向、Y向、绕X的旋转方向和绕Y的旋转方向解耦率均偏低。特别是绕X旋转方向，该方向是发动机激励的主要方向。该方向解耦率低会加剧系统振动恶化。因此，有待进一步提高。

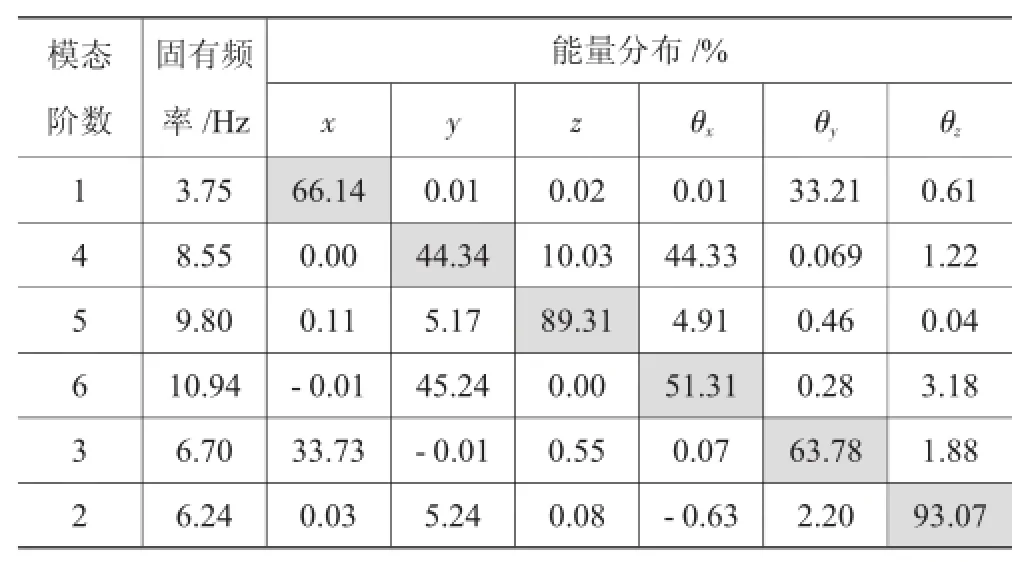
表3　优化前悬置系统的固有频率和能量分布

3.2优化设计

根据上述建立的系统振动微分方程和优化模型，采用序列二次规划算法SQP进行求解。对于该算法求解过程中容易陷入局部最优解的问题，采用取不同初始值的办法解决。优化后各悬置点在动力总成坐标系下的位置见表4；系统固有频率和能量分布见表5。各阶主振型方向的解耦率为表5中黑体所示。

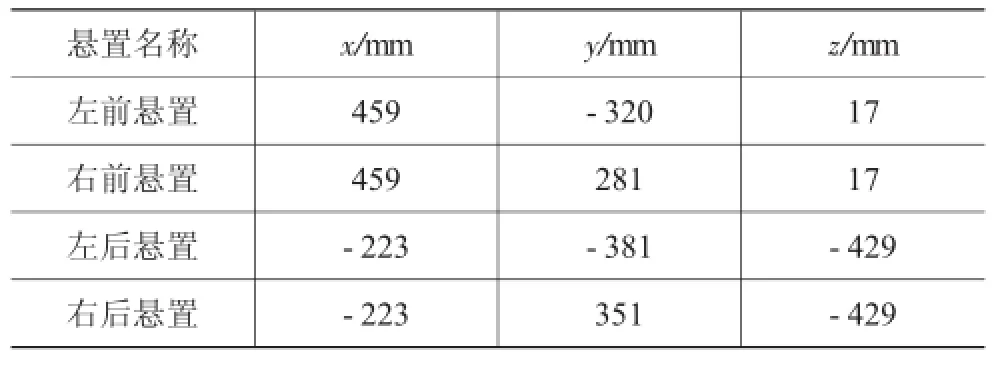
表4　优化后悬置元件坐标

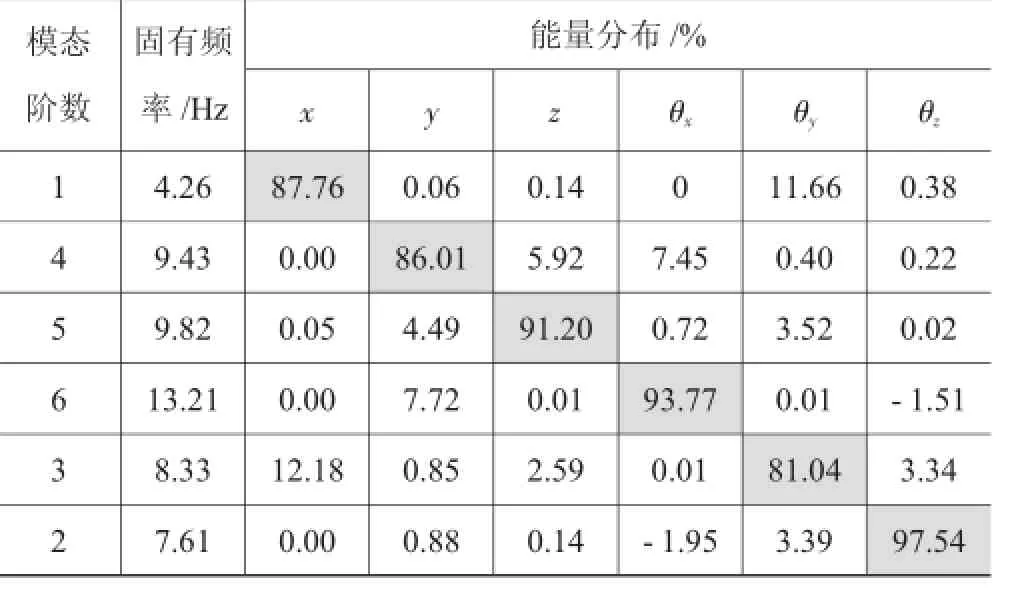
表5　优化后悬置系统的固有频率和能量分布

优化后悬置系统X方向的固有频率从3.75 Hz提高到4.26 Hz；解耦率各个方向均有提升，在对振动影响较大的Z向和绕X旋转方向解耦率达到90%以上，优化效果显著。X向的频率略微小于4.5 Hz，这是由于悬置点位置变化范围有限，最低频率难以再提升，考虑到X向传递的力较小，在优化过程中放宽一阶频率下限。

3.3优化前后振动响应分析

动力总成悬置系统的动态响应从另一个角度反映出悬置系统的隔振性能。对动力总成施加不同转速工况下发动机激振力［7］，比较优化前后悬置元件的传递力和动力总成质心处的加速度响应。根据微分方程（2），应用Newmark-β法求解微分方程［8］，得动力总成质心振动响应，位移、速度和加速度分别为x、x·、x¨。第i个悬置点的传递力响应函数为

将Fi减去静平衡下悬置点所受的力Fs；得到第i个悬置元件动态响应部分传递力：式中：ki为第i个悬置元件刚度矩阵；Ti为第i个悬置元件的方向转移矩阵；Bi为第i个悬置元件的位置转移矩阵［9］。

图2是优化前后左前悬置和左后悬置动态响应传递力均方根值曲线。由于左右悬置采用了相同的橡胶元件，而且在Y方向相对于发动机质心距离接近，左右悬置具有相近的力学特性。在此不列出前右悬置和后右悬置的曲线。图3为动力总成质心处振动加速度均方根值。

由图2可知，除了在低转速工况悬置元件的传递力在X方向略有增加，整体上优化后通过悬置元件向车身传递的力得到有效的改善。图3表明优化后动力总成质心处的振动有所减小。

4　结论

1）建立了悬置系统多目标优化设计模型，以悬置点的安装位置为设计变量对某款中型客车进行了优化设计，改善了系统的频率布置和提高了系统解耦率。

2）通过调整悬置元件的安装位置可以达到合理布置各阶振动频率和提高系统解耦率的效果，可以避免在某些改善设计中重新设计悬置元件导致的高成本和长周期的弱点。

3）从悬置系统的动态响应角度出发，对比分析了优化前后通过悬置元件向车身的传递力和动力总成质心处振动加速度，表明优化后悬置系统的隔振性能有一定程度的提高。

［1］Taeseok Jeong，Rajendra Singh.Analytical Methods of Decoupling the Automotive Engine Torque Roll Axis［J］.Journal of Sound and Vibration，2000，234（1）：85-114.

［2］史文库，洪哲浩，赵涛.汽车动力总成悬置系统多目标优化设计及软件开发［J］.吉林大学学报：工学版，2006，36（5）：654-658.

［3］J.H.金斯伯格.机械与结构振动［M］.白化同，李俊宝，译.北京：中国宇航出版社，2005.

［4］付江华，史文库，沈志宏，等.基于遗传算法的汽车动力总成悬置系统优化研究［J］.振动与冲击，2010，29（10）：187-190.

［5］温任林，颜景平.汽车发动机悬置系统多目标优化的研究［J］.东南大学学报，1996，26（6A）：105-111.

［6］Singiresu S.Rao.机械振动［M］.李欣业，张明路，译.北京：清华大学出版社，2009.

［7］张子庆，倪计民，石秀勇.路面激励对车用发动机动平衡特性的影响［J］.机械工程学报，2011，47（8）：134-140.

［8］郭泽英，李青宁.Newmark-精细积分方法的选择及稳定性［J］.世界地震工程，2008，24（3）：107-111.

［9］时培成.汽车动力总成悬置系统隔振分析与优化研究［D］.合肥：合肥工业大学，2010.

修改稿日期：2015-07-10

Optimization Design of a Coach Mounting System Based on Frequency Allocation and Decoupling Rate

Li Zhiqiang
（Xiamen KingLongUnited Automotive IndustryCo.，Ltd，Xiamen 361023，China）

The author establishes a 6-DOF model of the powertrain mounting system of a medium coach.He presents the optimization design model of the mounting system with the objective function for reasonable allocation of natural frequencies and decoupling rate to optimize and design the mounting system.By applying engine exciting force，the author compares the vibration response of mounting system before and after the optimization，the results showthat the optimization design is effective and feasible.

mountingsystem；natural frequency；decouplingrate；optimization design

U461.1

A

1006-3331（2015）06-0009-04

李智强（1988-），男，助理工程师；研究方向：动力总成悬置系统设计。