计及蓄电池储能寿命影响的微电网日前调度优化

杨艳红裴　玮　邓　卫　沈子奇　齐智平　周　勐

计及蓄电池储能寿命影响的微电网日前调度优化

杨艳红1,2裴玮1邓卫1沈子奇1齐智平1周勐3

（1. 中国科学院电工研究所 北京 100190 2. 中国科学院大学 北京 100190 3. 中国电力科学研究院 北京 100192）

蓄电池储能是进行微电网日前调度需要综合考虑的重要单元。为了充分发挥蓄电池储能平抑可再生能源波动、调节系统峰谷差及减小系统备用的功能，需要综合考虑其剩余容量、充放电功率及充放电次数对蓄电池寿命的影响。文中通过推导得出了反应蓄电池每一次放电损耗的数学模型，并对其进行了适当简化，通过权重因子将其引入到日前调度优化的目标函数中；针对蓄电池储能约束条件时间上耦合的特点，文中将基于拉格朗日松弛和内点法的动态规划方法应用于模型求解；通过算例分析，表明了所述方法对微电网日前调度具有良好的优化效果。

蓄电池寿命 微电网 优化 日前调度

0　引言

微电网集成太阳能光伏发电和风力发电等可再生能源发电、热电联供机组及储能装置，既可以向本地负荷供电，也可以通过公共连接点与外部电网进行功率交换[1]。在进行微电网日前调度时，蓄电池储能可以调节机组的功率输出以提高其运行效率，还可以利用分时电价实现电价差收益，从而优化系统整体运行经济性[2,3]。

蓄电池储能在运行时不直接产生运行费用，但其每一次充放电都会损耗使用寿命，文献[4,5]通过实验详细分析了蓄电池充放电深度和充放电速率对其寿命的影响。文献[6,7]将蓄电池储能寿命引入对其运行的影响，对以储能为主的独立运行风、光、柴和储系统运行中如何避免蓄电池储能在低荷电状态（SOC）下工作以及避免频繁充放电进行了研究，提出了采用充放电损耗假设影响因子的分析方法。对于联网运行的微电网系统，文献[8-10]的研究表明由于对接口功率的限制以及电价的变化，使其更加难于在考虑寿命影响的同时优化储能的功率和容量分配策略。对于如何评估储能寿命对微电网运行调度的影响，目前的研究往往采用简化的方式处理。计及蓄电池储能寿命影响的微电网日前调度问题从数学本质上讲是一个非线性的多阶段动态规划问题，既不宜引入过于复杂的储能模型，又需要能够真实反映储能寿命的影响，因此，对于建立适当的储能寿命模型尚需更为深入的研究。

在求解方面，文献[2]中采用了多步迭代粒子群（Particle Swarm Optimization, PSO）优化方法，文献[11]使用了改进遗传算法，文献[12]使用了主动进化规划的方法，分别对含有蓄电池储能的微电网系统调度进行了优化，使用智能算法的优点是可以精细建模，模型中可以包含不连续、非线性的约束，但其缺点是容易陷入局部最优且优化过程不可控、灵活性差。文献[3]和文献[13]以蓄电池荷电状态（State Of Charge, SOC）为状态变量使用动态规划方法对其实现削峰填谷的充放电策略进行了优化，而文献[14]使用动态规划方法对蓄电池参与调峰的容量与运行策略同时进行了优化，动态规划方法具有较快的计算速度和良好的收敛性。

综上所述，针对现有研究在考虑蓄电池储能寿命损耗模型和其在优化调度中的配合使用问题研究的不足，文中通过推导得出了反应蓄电池每一次放电损耗的数学模型，并对其进行了适当简化，通过权重因子将其引入到日前调度优化的目标函数中。针对蓄电池储能约束条件时间上耦合的特点，文中将基于拉格朗日松弛和内点法的动态规划方法应用于模型求解，通过算例分析，表明了所述方法具有良好的优化调度效果。

1　微电网系统电源模型

1.1微电网系统结构

如图1所示，典型的联网运行微电网系统，其中的发电单元包括太阳能光伏发电、风力发电、微型燃气轮机发电和燃料电池发电，均通过电力电子变换器接入交流母线，交流母线配置一定容量的储能装置，整个系统优先给本地负荷供电，并通过PCC与外部大电网相连。

在进行微电网日前调度时，应大致遵循以下原则：

（1）太阳能光伏发电、风力发电作为可再生能源优先使用，如果其发电功率大于本地负荷，可以考虑向蓄电池充电或向电网反送部分电能。

（2）微型燃气轮机和燃料电池输出功率稳定、响应速度快，作为可调度发电单元，其出力情况主要受经济性制约，尽量保证其工作在较高的负荷率。

（3）蓄电池储能可以平抑微电网功率波动，提高电能质量；也可以调节峰谷差，获取经济收益；还可以作为后备电源。蓄电池储能的运行经济性与其寿命息息相关。

（4）满足微电网与外部电网接口交换功率要求。

图1　典型联网运行的微电网系统Fig.1　A typical microgrid of networking operation

1.2太阳能光伏发电模型

太阳能光伏发电模型是为了计算得到其日前功率输出曲线。日前太阳能光伏发电的预测可以分为统计类方法和物理类方法，考虑缺乏历史数据的因素，文中使用Osterwald物理类预测方法[15]具体过程如下。

根据气象局发布的日前气象、辐射和温度数据计算太阳能光伏发电的功率输出

式中，PSTC为标准测试条件下的最大测试功率；GSTC为标准测试条件下的光照强度；GT为实际太阳能辐射强度；k为功率温度系数，取-0.004 7/℃；Tc为电池板工作温度；Tr为参考温度，取为25℃。

太阳能电池板的工作温度Tc可以根据经验公式进行估算

式中，aT为环境温度。

1.3风力发电模型

风力发电日前功率输出曲线可以通过风速预测和风速-功率曲线拟合两步得到。日前风速预测可以通过气象预报和现有的方法得到[16,17]。

一般厂家会给出风力发电机组的风速-功率测试数据，通过式（3）拟合得出任意风速的功率输出值。

式中，inv、nv和outv分别为切入风速、额定风速和切出风速；wtnp为额定功率；a、b、c和d四个参数根据风速-功率曲线拟合。

1.4微型燃气轮机发电模型

微型燃气轮机作为可调度发电单元，输出功率稳定，响应速度快，可以满足负荷突变要求，但其发电效率低，一般需要热电联供才能满足经济性要求。本文考虑微型燃气轮机优先满足发电要求，参与系统日前调度，即“以电定热”方式运行，余热回收纳入经济评价。

微型燃气轮机的发电效率与输出功率之间的关系为

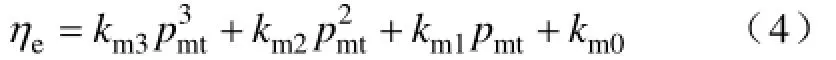
式中，m3k、m2k、m1k和m0k为电功率-效率拟合系数；mtp为微型燃气轮机实际输出电功率。

回收微型燃气轮机的排气余热，在进行热电联供时系统的总效率为[18]式中，η为系统总效率；recQ为微型燃气轮机回收的排气余热量；fm为燃料流量；gL为天然气的低热值，gL=9.773kW h/m·。微型燃气轮机的燃料成本计算公式为

式中，gc为天然气价格；efη为微型燃气轮机的等效发电效率。

1.5燃料电池发电模型

燃料电池堆是由多个单电池通过串联封装而成，其发电效率依赖于工作点，燃料电池的燃料成本为[19]

式中，fcp为燃料电池的输出功率；fcη为燃料电池的发电效率。

2　蓄电池储能的模型

微电网在进行日前调度优化时需要合理的蓄电池储能模型，以全面反映储能的功率输出能力、能量存储能力、经济性、使用寿命和充放电损耗之间的关系[20]。

蓄电池的功率输出能力以其放电功率的大小来衡量，其与蓄电池的能量存储能力（以电池荷电状态来衡量）的关系为

式中，SOC为蓄电池的荷电状态；essp为蓄电池的放电功率；cη为蓄电池的放电效率；essC为蓄电池的额定容量。

蓄电池储能的寿命和损耗与它的荷电状态和充放电功率密不可分。根据Symons的假设1，蓄电池的寿命可以表示成蓄电池可供使用的有效吞吐量之和（A·h数），有效的A·h数可以通过使用假设2、3修正实际A·h数而得到[21]。当累积的有效A·h数达到电池额定寿命时，电池报废。蓄电池额定的可供使用吞吐量为

式中，RC为额定容量（在额定放电电流RI下）；RD为额定放电深度，用来确定额定循环寿命；RL为额定放电深度RD和额定放电电流RI下的额定循环寿命。（所谓的额定状态是指蓄电池的温度、浮压工作在其出厂的额定设置，蓄电池做定期升压充电维护等。）

通过对蓄电池的实验数据分析可以得出影响其寿命的两个关键因素：放电深度和放电速率与蓄电池使用寿命的大致函数关系[4]。

2.1蓄电池放电深度的影响

每个放电循环计算放电深度对电池寿命的影响，然后通过拟合实验数据可以得到蓄电池放电深度与实际循环寿命的关系，如图2所示[4]。计算公式为

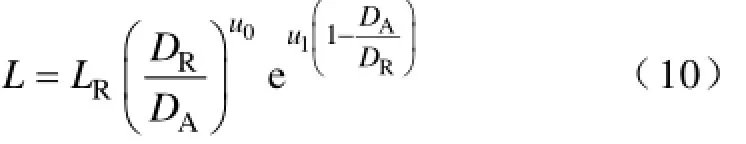
图2　蓄电池放电深度对实际循环寿命的影响Fig.2 Influence of DOD on the cycle life

等效放电的A·h数与实际放电的A·h数关系为

将式（11）代入到式（10），整理后可以得到effd的计算公式为

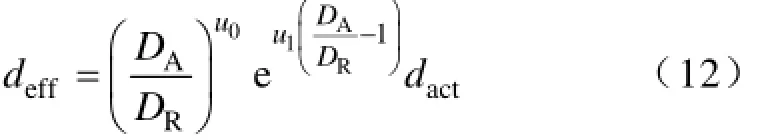
式中，L为实际循环寿命；effd有效放电A·h数；actd实际放电A·h数；AD实际放电深度；0u、1u为电流拟合参数。

2.2蓄电池放电速率的影响

高放电速率会导致蓄电池低电导率和快速的腐蚀，使其实际功率输出能力下降，如图3所示[4]。

通过实验数据得知，有效放电A·h数与实际放电A·h数的关系如下

式中，AC为实际放电容量，可以通过蓄电池出厂使用手册查询。

图3　蓄电池放电速率对实际容量的影响Fig.3　Affect of discharge current to actual capacity

综合放电深度和放电速率对蓄电池寿命的影响，可以得到一次放电消耗掉的有效A·h数的表达式为

如果已知蓄电池初始投资，从而可以计算蓄电池一次放电的寿命损耗花费为

式中，cdc为蓄电池一次放电的寿命损耗花费；cRc为蓄电池的初始投资。

蓄电池在某种使用模式下，如果在时间段T内包含n个放电事件，实际使用过程中的电池寿命如下

式中，CR、DR、LR和T为均为常数，预想使电池的寿命最大，(i )应该最小。

在进行日前调度时，直接应用式（14）优化计算过于复杂，对其进行如下化简：

（1）首先，由于DA=1- SOC ，将式（14）写成

（2）式（17）中容量比

（3）将式（18）代入（17）并化简，得到

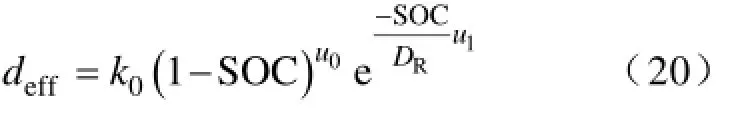
（5）对式（20）的指数函数部分进行泰勒级数展开为

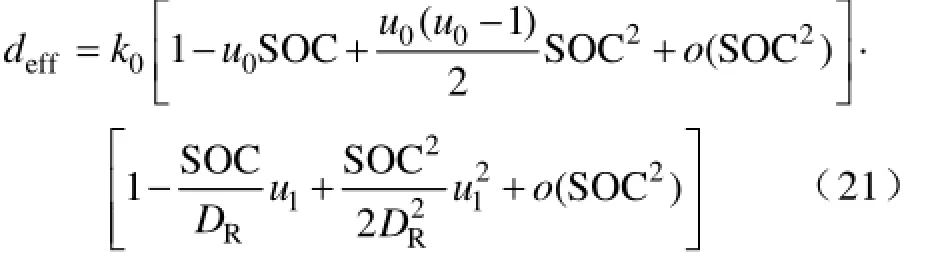
（6）对式（21）化简，省去高阶无穷小，并令

则有

式中，1k、2k和3k均为常数；effd是SOC的二次函数。

3　日前调度优化模型

微电网日前调度方案是针对负荷和可再生能源发电预测曲线制定下一日的运行计划，需要综合考虑系统经济运行和可靠性方案，蓄电池储能对系统方案的制定有着重要影响，很难依照常规经验制定蓄电池储能的使用策略。根据对储能使用寿命的不同考虑可以建立以下两种模型。

3.1不考虑储能寿命影响的优化模型

不考虑蓄电池寿命影响时，以微电网系统日运行费用最小为优化目标，蓄电池储能在系统运行时不产生直接的运行费用，不计入目标函数。这种模型可以直接优化出系统日运行最小费用，缺点是可能影响储能寿命，致使其提前报废。

目标函数

约束条件

（1）发电单元j在t时刻的功率输出

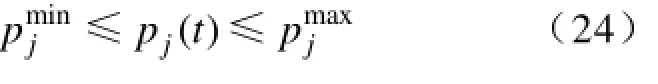
（2）发电与负荷供需平衡

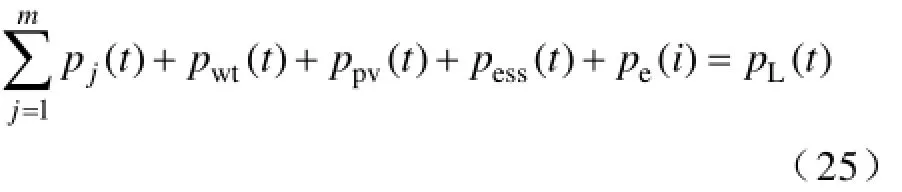
（3）储能功率输出

（4）储能荷电状态约束

（5）电网接口功率约束，主要考虑到微电网与外部电网功率交换在一些情况下受到配电网调度管理的限制。

3.2计及储能寿命损耗的优化模型

微电网系统调度蓄电池储能平抑可再生能源波动或削峰填谷时，都会损耗储能自身的寿命，利用第2节中的推导，将式（22）代入式（15），则得到蓄电池一次放电的寿命损耗花费为

将式（30）右端写成SOC的函数形式(SOC)f，同时引入考虑储能寿命损耗的权重因子λ，加入储能寿命损耗花费后的目标函数如下

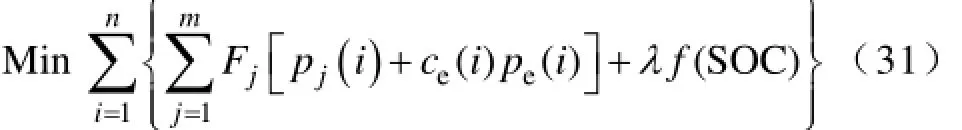
约束条件与3.1节不考虑储能寿命影响的约束相同。

4　求解方法

4.1动态规划方法

动态规划所处理的问题是一个多阶段决策问题，其理论基础是最优性理论，常用的动态规划逆序求解基本方程如下

式中，xk为第k阶段的状态变量；uk为第k阶段的决策变量；vk（xk,uk）为第k阶段的指标函数；k=1,2,…,N ，N为规划阶段总数。

4.2日前调度优化模型的求解

微电网日前调度问题是典型的多阶段决策过程，以每小时为调度间隔为例，日前调度过程可以分为24个阶段决策过程。在进行每个阶段决策时，不仅仅要考虑阶段指标，因为本阶段的决策将会对下面的阶段产生影响，应该考虑从本阶段直至最后一个阶段的总指标；决策时储能只依赖与上一个阶段的存储量，而和以前的存储过程无关，满足无后效性要求。

令kx为状态变量，表示可调度机组的功率输出；ku为决策变量，表示可调度机组的决策调整；函数kv为阶段指标方程；函数kg为状态转移方程。则微电网日前调度的动态规划模型可以写成式（33）～式（36）。

目标函数

约束条件

式中，Ekc、ENc表示等式约束；Ikc、INc表示不等式约束。

上述动态规划模型式（33）～式（36）中变量的最高次项为二次，可以采用文献[22]所述的通过引入拉格朗日因子并采用内点法处理不等式约束，形成序列二次规划子问题，然后迭代求解，从而提高算法的收敛速度。其求解流程如图4所示。

5　算例分析

以某联网运行的建筑级微电网为例进行算例分析，其装机情况见表1，蓄电池储能的详细参数与配置情况见表2。系统的日前负荷预测结果，日前太阳能光伏发电预测结果，日前风力发电预测结果如图5所示。

图4　逆序动态规划的流程Fig.4　Flow chart of reverse dynamic programming

表1　系统装机情况Tab.1 Distribution of active power and reactance

表2　蓄电池储能的详细参数Tab.2　Distribution of active power and reactance

考虑到配电网调度管理的限制，微电网与外部电网接口功率限制在平均负荷的0～10%。外部电网电价如图6所示。天然气的价格为2.05元/3m。蓄电池的装机成本按照1 000元/(kW.h)计算，蓄电池储能次日初始取SOC=0.3。

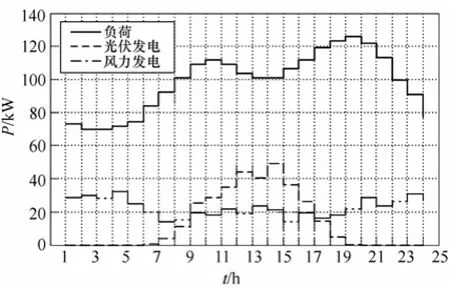
图5　日前功率预测Fig.5　Day-ahead power forecast

图6　外部电网电价Fig.6　Power price of the external grid

不考虑储能寿命损耗对微电网运行的影响和采用文中所述计及储能寿命影响的优化计算结果如下：

（1）不考虑储能寿命损耗时的优化结果。此时，上述微电网系统日运行费用最小为775.35元；可调度单元的功率输出情况如图7所示，由图可知蓄电池储能在外部电网低价时利用其进行充电，外部电网高价时放电，从而实现倒电价差收益。同时在低负荷时利用燃料电池和微燃机对蓄电池进行充电，高负荷时放出，从而使得机组始终在额定功率高效运行。蓄电池动态SOC变化情况如图8所示，SOC运行在较低状态，频繁充放电，变化比较剧烈。

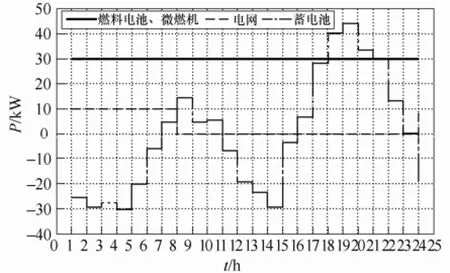
图7　微电网功率调度情况Fig.7　Power scheduling of the microgrid without battery life consideration

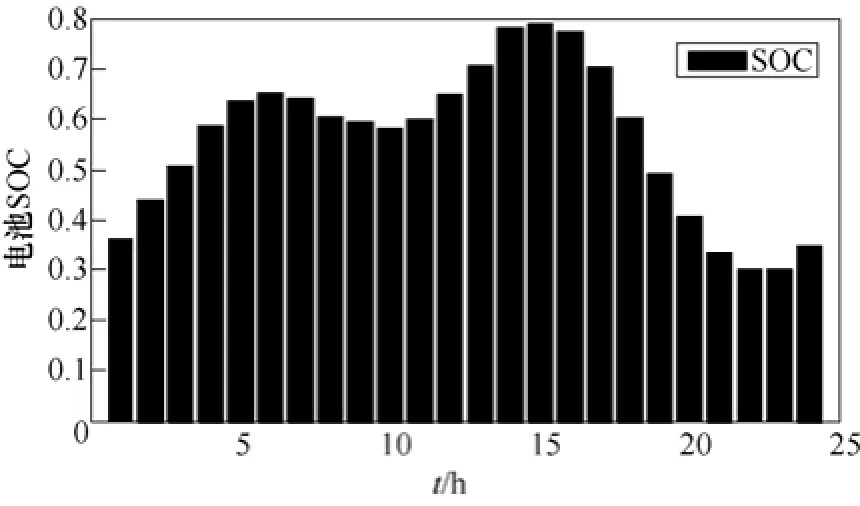
图8　蓄电池SOC状态Fig.8　SOC of the battery without battery life consideration

（2）计及储能寿命影响的优化计算结果。此时，上述微电网系统日运行费用最小为975.5元（λ=0.4），储能寿命损耗费用占总费用的13.1%。此时可调度单元的功率输出情况如图9所示，与图7相比，储能在进行削峰填谷获取电价差收益的同时，受到自身SOC状态和放电速率的约束从而延长自身使用寿命；蓄电池储能动态SOC变化情况如图10所示，与图8相比，其运行在较高的SOC状态，并且充放电较为平缓。

图9　计及储能寿命时微电网功率调度情况Fig.9　Power scheduling of the microgrid with battery life consideration

图10　计及蓄电池SOC状态Fig.10　SOC of the battery with battery life consideration

对比上述两种优化结果，文中所述计及储能寿命影响的微电网日前调度模型能够更好地优化系统调度，在获取最优运行经济性的同时对蓄电池储能的运行状态进行了优化，从而可以延长其使用寿命，取得间接的经济效益。方案（1）中蓄电池储能日累计放电225kW·h，而方案（2）中蓄电池储能日累计放电160.5kW·h，方案（2）比方案（1）减少了28.7%的蓄电池储能损耗。

权重因子λ代表了系统调度时对蓄电池储能寿命的重视程度，λ越大，调度时越应该减少储能的使用，λ与蓄电池储能日累计放电量的关系如图11所示。

图11　权重因子λ对蓄电池使用的影响Fig.11　Influence of λ on the battery use

6　结论

本文通过推导得出了反应蓄电池储能每一次充放电损耗的数学模型，适当简化后通过权重因子将其引入到微电网日前调度目标函数中。针对蓄电池储能约束条件时间上耦合的特点，文中将基于拉格朗日松弛和内点法的动态规划方法应用于模型求解。通过对算例的计算与分析，表明了本文所述方法对解决考虑蓄电池储能寿命影响的微电网日前调度问题具有良好的优化效果。

[1] Lasseter R H. Integration of distributed energy resources: The CERTS microgrid concept[R]. Consortium for Electric Reliability Technology Solutions, 2002.

[2] Lee T Y. Operating schedule of battery energy storage system in a time-of-use rate industrial user with wind turbine generators: a multipass iteration particle swarm optimization approach[J]. IEEE Transactions on Energy Conversion, 2007, 22(3): 774-782.

[3] Liu Xiaoping, Ding Ming, Han Jianghong, et al. Dynamic economic dispatch for microgrids including battery energy storage[C]. IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), 2010: 914-917.

[4] Drouilhet S, Johnson B L. A battery life prediction method for hybrid power applications[C]. AIAA Aerospace Sciences Meeting and Exhibit, 1997.

[5] Schiffer J, Sauer D U, Bindner H, et al. Model prediction for ranking lead-acid batteries according to expected lifetime in renewable energy systems and autonomous power-supply systems[J]. Journal of Power Sources, 2007, 168(1): 66-78.

[6] 陈健, 王成山, 赵波, 等. 考虑储能系统特性的独立微电网系统经济运行优化[J]. 电力系统自动化, 2012, 36(20): 25-31. Chen Jian, Wang Chengshan, Zhao Bo, et al. Economic operation optimization of a stand-alone microgrid system considering characteristics of energy storage system[J]. Automation of Electric Power Systems, 2012, 36(20): 25-31.

[7] Zhao B, Zhang X, Chen J, et al. Operation optimization of standalone microgrids considering lifetime characteristics of battery energy storage system[J]. IEEE Transactions on Sustainable Energy, 2013, 4(4): 934-943.

[8] 丁明, 张颖媛, 茆美琴. 包含钠硫电池储能的微网系统经济运行优化[J]. 中国电机工程学报, 2011, 31(4): 7-14. Ding Ming, Zhang Yingyuan, Mao Meiqin, et al. Economic operation optimization for microgrids including Na/S battery storage[J]. Proceedings of the CSEE, 2011, 31(4): 7-14.

[9] Gu W, Wu Z, Yuan X. Microgrid economic optimal operation of the combined heat and power system with renewable energy[C]. IEEE Power and Energy Society General Meeting, 2010: 1-6.

[10] 陈昌松, 段善旭, 蔡涛, 等. 基于改进遗传算法的微网能量管理模型[J]. 电工技术学报, 2013, 28(4): 196-201. Chen Changsong, Duan Shanxu, Cai Tao, et al. Microgrid energy management model based on improved genetic arithmetic［J］. Transactions of China Electrotechnical Society, 2013, 28(4): 196-201.

[11] Chacra F A, Bastard P, Fleury G, et al. Impact ofenergy storage costs on economical performance in a distribution substation[J]. IEEE Transactions on Power Systems, 2005, 20(2): 684-691.

[12] Cau T D H, Kaye R J. Multiple distributed energy storage scheduling using constructive evolutionary programming[C]. Proceedings of IEEE Power Engineering Society International Conference on Power Industry Computer Applications, Sydney, Australia, 2001: 402-407.

[13] Maly D K, Kwan K S. Optimal battery energy storage system (BESS) charge scheduling with dynamic programming[J]. IEE Proceedings Science, Measurement and Technology, 1995, 142(6): 453-458.

[14] Oudalov A, Cherkaoui R, Beguin A. Sizing and optimal operation of battery energy storage system for peak shaving application[C]. IEEE Proceedings of Power Tech, Lausanne, Switzerland, 2007: 621-625.

[15] Osterwald C R. Translation of device performance measurements to reference conditions[J]. Solar Cells, 1986, 18(3-4): 269-279.

[16] 白龙, 吴息, 丁宇宇, 等. 用于风电场功率预测的逐时风速预报[J]. 气象科技, 2013, 41(4): 777-783. Bai Long, Wu Xi, Ding Yuyu, et al. Hourly wind speed forecasting for wind farm prediction[J]. Meteorological Science and Technology, 2013, 41(4): 777-783.

[17] 罗文, 王莉娜. 风场短期风速预测研究[J]. 电工技术学报, 2011, 26(7): 68-74. Luo Wen, Wang Lina. Short-term wind speed forecasting for wind farm[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 68-74.

[18] Boncompagni S C, Macchi E. Microturbines and trigeneration: optimization strategies and multiple engine configuration effects[J]. Journal of Engineering for Gas Turbines and Power, 2004, 126(1): 92-101.

[19] 杨秀, 陈洁, 朱兰, 等. 基于经济调度的微网储能优化配置[J]. 电力系统保护与控制, 2013, 41(1): 53-60. Yang Xiu, Chen Jie, Zhu Lan, et al. Optimization allocation of energy storage for microgrid based on economic dispatch[J]. Power System Protection and Control, 2013, 41(1): 53-60.

[20] Manwell J F, McGowan J G. Lead acid battery storage model for hybrid energy systems[J]. Solar Energy, 1993, 50(5): 399-405.

[21] Symons P. Life estimation of lead-acid battery cells for utility energy storage[C]. Proceedings of the Fifth Conference on Batteries for Utility Storage, San Juan, Puerto Rico, 1995.

[22] Dohrmann C R, Robinett R D. Dynamic programming method for constrained discrete-time optimal control[J]. Journal of Optimization Theory and Applications, 1999, 101(2): 259-283.

杨艳红 男，1985年生，博士研究生，主要从事微网规划设计与运行控制的研究。

裴 玮 男，1982年生，副研究员，主要从事含分布式能源的电力系统分析、微电网运行控制和智能电网的研究。

Day-Ahead Scheduling Optimization for Microgrid with Battery Life Model

Yang Yanhong1,2Pei Wei1Deng Wei1Shen Ziqi1Qi Zhiping1Zhou Meng3
（1. Institute of Electrical Engineering Chinese Academy of Science Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100190 China 3. China Electric Power Research Institute Beijing 100192 China）

Battery energy storage is an important element to be considered when the day-ahead dispatch of microgrid is carried out. In order to maximize the abilities of battery energy storage for stabilizing the fluctuations of renewable energy, regulating the difference between peak and valley and reducing the back capacity, the impacts on the battery life need to be considered, such as remaining capacity, charge power discharge power and the number of use times. In this paper, the mathematical model of each battery discharge loss is established. Before the model is introduced into the scheduling optimization objective function appropriate simplification is carried out by the weighting factor. For the characteristics of battery energy storage constraints coupled in continuous time, the Lagrangian relaxation and interior point method are introduced to solve dynamic programming model. The numerical example shows that the proposed method has good optimization results.

Battery life, optimization, microgrid, day-ahead scheduling

TM76

国家自然科学基金面上项目（51277170），国家自然科学青年基金（50907065）和中国科学院知识创新工程重要方向项目（KGCX2-EW-322）资助。

2013-11-15 改稿日期 2014-02-10