考虑发热限制的双余度无刷直流电机 定子裂比优化方法

李全武　窦满峰

考虑发热限制的双余度无刷直流电机 定子裂比优化方法

李全武窦满峰

（西北工业大学自动化学院 西安 710072）

针对一种航空机电作动器用双余度无刷直流电机在外形尺寸及发热限制下的转矩提升问题，提出一种新型的双余度无刷直流电机定子裂比优化方法。该优化方法通过限定铜耗密度以限制电机整体发热，限定电流密度以限制绕组局部发热，以发热限制为电磁转矩边界，针对单绕组工作冷备份与双绕组工作热备份两种备份方式，通过分析电磁转矩与定子裂比的关系，推导得出两种备份方式使电磁转矩最大的最优定子裂比表达式。利用有限元仿真对最优定子裂比解析值进行了验证，误差小于2%；依照本方法试制出样机，样机电磁转矩测试值与解析值相比误差为9.3%。仿真及测试结果表明，所提出的新型定子裂比优化方法可在双余度无刷直流电机外形尺寸一定、限制发热条件下，使转矩得到充分提升。

双余度 无刷直流电机 定子裂比 发热限制

0　引言

机电作动器（Electromechanical Actuator，EMA）具有体积小、结构简单、效率高、无泄漏和可靠性高等特点，是航空电力作动器发展的重要方向［1］。航空EMA对其电动机外形尺寸有严格限制，且要求电动机具备高可靠性，同时需要电机具备输出足够力矩的能力，以满足EMA驱动需求。

双余度无刷直流电机（Dual-Redundancy Brushless DC Motor，DRBLDCM）有两套绕组，与控制系统形成独立通道，在航空高可靠性要求场合，如作动器、舵机和阀门等中有应用［2，3］。DRBLDCM分为冷备份和热备份两种备份方式。正常情况冷备份单绕组工作，发生故障则切换至另一套工作；热备份正常时双绕组工作，一套故障则由另一套全载工作［4］。

电枢绕组是电机的薄弱环节，绕组故障对电机性能会产生严重影响［5-7］。绕组故障主要由铜耗密度超限致使定子整体过热，或由电流密度超限使绕组局部过热引起［8-11］。DRBLDCM采用绕组备份可提高可靠性，但两绕组为相似备份，同一故障可能使两绕组相继失效，未解决根本问题。若在DRBLDCM设计中限定铜耗密度和电流密度以限制发热，同时保证力矩输出，可进一步提高电机可靠性。

定子裂比为定子铁心内、外径之比，是电机设计的重要参数。文献［12］在铜耗一定情况下，提出一种永磁无刷电机转矩密度最大化的定子裂比优化方法。文献［13］对比研究了电励磁和永磁同步电机转矩密度优化的定子裂比优化方法。文献［14］提出一种内嵌式永磁无刷电机定子裂比优化方法。文 献［15］研究了内、外转子永磁无刷电机定子裂比优化方法。上述方法在一定热限制条件下，通过优化定子裂比提高电磁转矩，未涉及同时限制铜耗密度和电流密度下，双余度无刷直流电机的转矩提升问题。

DRBLDCM在一定外形尺寸、散热方式、绝缘等级和工作制等条件下，可承受的整体和局部发热一定，设计中需限制与发热相关的铜耗密度和电流密度，通过分析二者与定子裂比、电磁转矩的关系，推导得出限制铜耗密度和电流密度时电磁转矩最大时对应的最优定子裂比，从而实现发热限制下转矩的提升，并利用有限元仿真和实验进行验证。

1　分析模型

本文以一种12槽10极内转子DRBLDCM为研究对象，样机有两套电气上相互独立的三相绕组A1、B1、C1和A2、B2、C2，对应相差30°，节距为1，集中绕组，联结，如图1所示。图中，Aij表示绕 组i的第j个元件线圈；Do和Ds分别为定子铁心外径和内径。样机主要参数见表1。

图1　12槽10极DRBLDCM结构及绕组形式Fig.1　Structure and coil of a 12 slots 10 poles DRBLDCM

表1　样机主要参数Tab.1 Main constant parameters of the prototype

热负荷q表示电机整体发热程度及热承受能力，其定义为散热面单位面积的损耗。样机为封闭式，通过定子外表面散热，考虑主要损耗铜耗和铁耗，则样机q的表达式为

式中 PCu——绕组有效部分（铁心内）铜耗；

PFe——定子铁耗；

Do——定子铁心外径；

lef——定子铁心长度。

本文主要研究中、低速电机，样机额定频率为333.3Hz，铁耗约为铜耗的1/4，铜耗为主要损耗，如图2所示为定子裂比对样机铁耗的影响。图中，在常用定子裂比区间0.3～0.7内，定子裂比对铁耗无明显影响，与文献［16］结论一致。随着定子裂比变化，q主要受铜耗密度qCu（见式（2））影响，通过限制qCu可达到限制q及电机整体发热的目的。

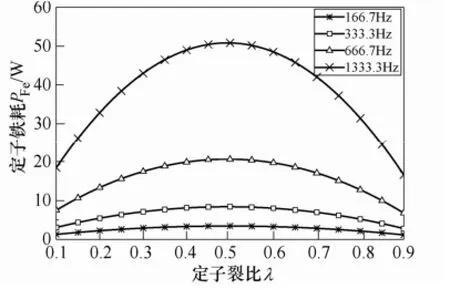
图2　定子裂比对样机铁耗的影响Fig.2 Iron loss variation with split ratio of the prototype

DRBLDCM电流密度J表达式为

式中 Ia——电枢电流；

Acond——单根导体截面积。

电流密度反映了单根导体的铜耗密度情况，限制J则可限制绕组局部发热。

定子冲片简化分析模型如图3所示，其中图3a为实际外形，图3b为简化模型，图中bt为定子齿部宽度，bj为定子轭部宽度，As为定子槽面积。

图3　定子简化分析模型Fig.3　Simplified stator analytical model

本文主要研究在无故障及相同发热限制条件下，热备份双绕组工作方式和冷备份单绕组工作方式的最优定子裂比。文中将用双绕组工作指代热备份方式，用单绕组工作指代冷备份方式。

2　DRBLDCM电磁转矩表达式

2.1电磁转矩与铜耗密度关系

DRBLDCM单匝线圈所受电磁力为

式中 Bδ——气隙磁通密度。

电机同一时刻两相导通，转子所受电磁力

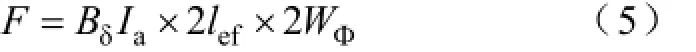
式中 WΦ——单绕组每相串联匝数。

冷备份单绕组工作电磁转矩Tem1为

式中 Ds——定子铁心内径。

冷备份单绕组工作的铜耗

式中Cuρ——铜的电阻率。

单根导体截面积Acond表达式为

式中 As——定子槽面积；

ks——槽满率；

Q——定子槽数。

联立式（2）、式（6）～式（8），限制最大允许铜耗密度为qCu.max，单绕组电磁转矩表达式为

式中 λ——定子裂比，λ=Ds/Do；

β ——磁通密度系数，β=Bδ/Bmax；

Bmax——定子最大磁通密度。

限制双绕组方式最大铜耗密度为qCu.max，则各单套绕组的最大铜耗密度为qCu.max/2。双绕组电磁转矩Tem2为单套绕组限制qCu.max/2时电磁转矩的叠加，即

2.2电磁转矩与电流密度关系

联立式（3）、式（6）～式（8），限定绕组最大允许电流密度为Jmax，单绕组电磁转矩表达式为

双绕组工作最大允许电流密度仍为Jmax，双绕组电磁转矩为单绕组电磁转矩的叠加，即

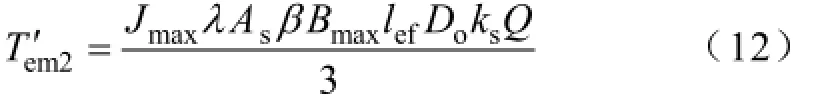
3　最优定子裂比的计算

3.1定子槽面积表达式

式（9）～式（12）中定子槽面积As为变量，As受Ds影响，即与λ有关，需分析As与λ的关系。

气隙磁通密度为Bδ，定子齿磁通密度为Bmax，一个齿距内，定子齿部磁通与气隙磁通相同。即

可得定子齿宽bt的表达式

12槽10极DRBLDCM定子轭部磁通为齿部的1/2，两处磁通密度相同，故轭宽bj为齿宽bt的1/2，即

由图3b所示定子几何关系及式（14）、式（15），得到As表达式为

式中，λ2的系数ζa，λ 的系数ζb分别为

系数k为槽数与极对数之比

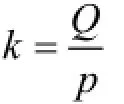
3.2限制铜耗密度的最优定子裂比

限制铜耗密度，根据式（9）和式（10），单绕组和双绕组最优定子裂比相同，故以单绕组为例研究。

得到λop1表达式为

式中

由式（18）可知，λop1与磁通密度系数β 和极对数p有关，由式（18）得图4。可看出：β 不变，λop1随p增大而增大；相同p，λop1随β 增大而减小。

图4　限定qCu，不同p情况，β 对λop1的影响Fig.4　Variations of λop1with β at different p when qCuis limited

将As表达式代入式（9），得到限定铜耗密度下单绕组电磁转矩与定子裂比的关系表达式为

限定样机qCu.max=4kW/m2、Bmax=1.5T，由式（19）得图5。由图5可知：存在最优定子裂比；气隙磁通密度越大，最优定子裂比越小，最大电磁转矩越高。

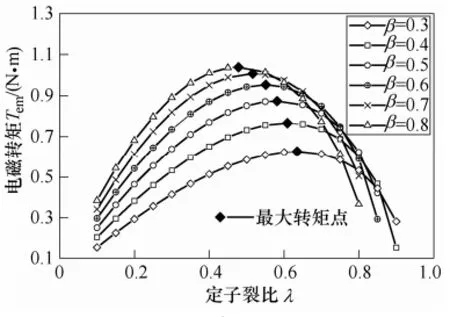
图5　限定qCu.max=4kW/m2，不同β，λ 对Tem的影响Fig.5　Variations of Temwith λ at different β when qCu.max=4kW/m2

3.3限制电流密度的最优定子裂比

根据式（11）和式（12），限制电流密度，单绕组和双绕组最优定子裂比相同，故以单绕组为例 研究。

得出λop2表达式

式中

由式（21）得图6，图中最优定子裂比随β 和p变化趋势与图4相似。

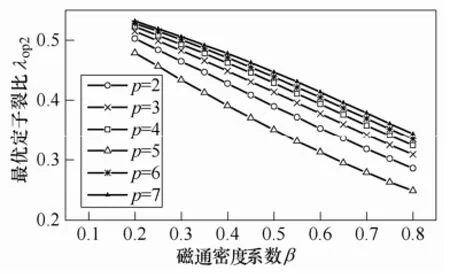
图6　限制J，不同p情况，β 对λop2的影响Fig.6　Variations of λop2with β at different p when J is limited

将As表达式代入式（11），得到限定电流密度下单绕组电磁转矩与定子裂比的关系表达式限定Jmax=15A/mm2、Bmax=1.5T，由式（22）得图7。由图7可知：存在最优定子裂比；气隙磁通密度越大，最优定子裂比越小，最大电磁转矩越高。

图7　限定Jmax=15A/mm2，不同β，λ 对Tem的影响Fig.7　Variations of Temwith λ at different β when Jmax=15A/mm2

3.4限制铜耗密度及电流密度的最优定子裂比

3.2节和3.3节研究了分别限制铜耗密度和电流密度单绕组工作的最优定子裂比，实际设计中应同时限制二者。同时作qCu.max=4kW/m2、Jmax=15A/mm2和β =0.4的电磁转矩-定子裂比曲线，如图8所示。

图8 满足qCu和J限制的定子裂比可选区域Fig.8　Region where λ satisfying qCuand J limitation

图8中可选区域λ同时满足铜耗密度和电流密度限制，该区域电磁转矩最大点（图8中两曲线交点）对应λ 为最优定子裂比，该情况下单绕组工作最优定子裂比λop3的表达式为

式中

3.5热备份双绕组工作的最优定子裂比

单独限制铜耗密度或电流密度时，双绕组工作电磁转矩与单绕组工作电磁转矩为倍数关系，二者最优定子裂比相同，单独限制铜耗密度时均为λop1，单独限制电流密度时均为λop2。

同时限制铜耗密度和电流密度，最大转矩点为两电磁转矩-定子裂比曲线的交点（见图8所示），单绕组工作与双绕组工作的最优定子裂比不同，双绕组工作最优定子裂比λop4表达式为

式中

3.6最优定子裂比的选择

DRBLDCM铜耗密度和电流密度限定值的选择应综合考虑电机体积重量、散热方式、绝缘等级和工作制等因素。以上因素不同，限定值不同，单绕组和双绕组工作的最优定子裂比可能不同。

限定qCu.max=4kW/m2、Jmax=15A/mm2，单绕组最优定子裂比为λop3，双绕组最优定子裂比为λop1，如图9所示。

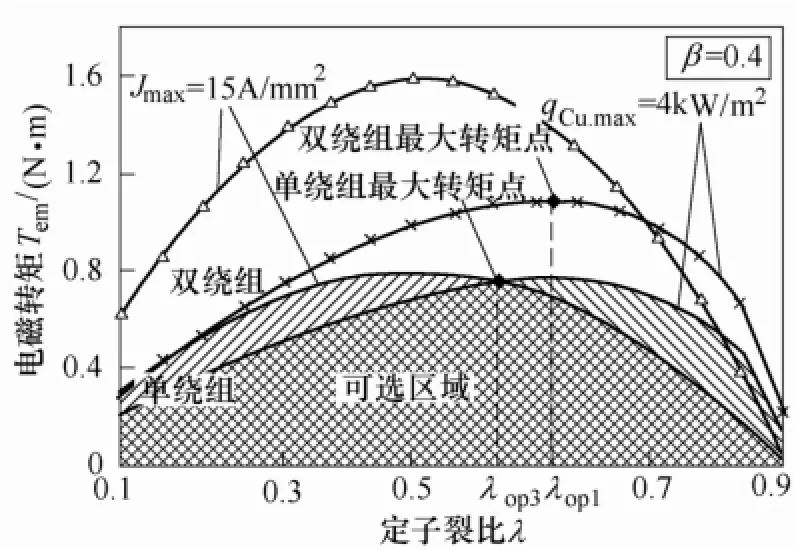
图9　限定qCu.max=4kW/m、Jmax=15A/mm， DRBLDCM的最优定子裂比Fig.9　Optimal split ratio of DRBLDCM when qCu.max=4kW/m2and Jmax=15A/mm2

限定qCu.max=2.5kW/m2、Jmax=15A/mm2，单绕组与双绕组最优定子裂比均为λop1，如图10所示。

限定qCu.max=4kW/m2、Jmax=10A/mm2，单绕组最优定子裂比为λop2，双绕组最优定子裂比为λop4，如图11所示。

冷备份方式最优定子裂比取值范围为λop1、λop2和λop3，热备份方式最优定子裂比取值范围为λop1、λop2和λop4。相同发热限制条件，两备份方式最优定子裂比可能不同。

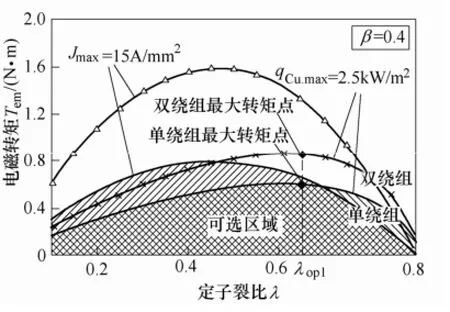
图10　限定qCu.max=2.5kW/m2、Jmax=15A/mm2，DRBLDCM的最优定子裂比Fig.10　Optimal split ratio of DRBLDCM when qCu.max=2.5kW/m2and Jmax=15A/mm2

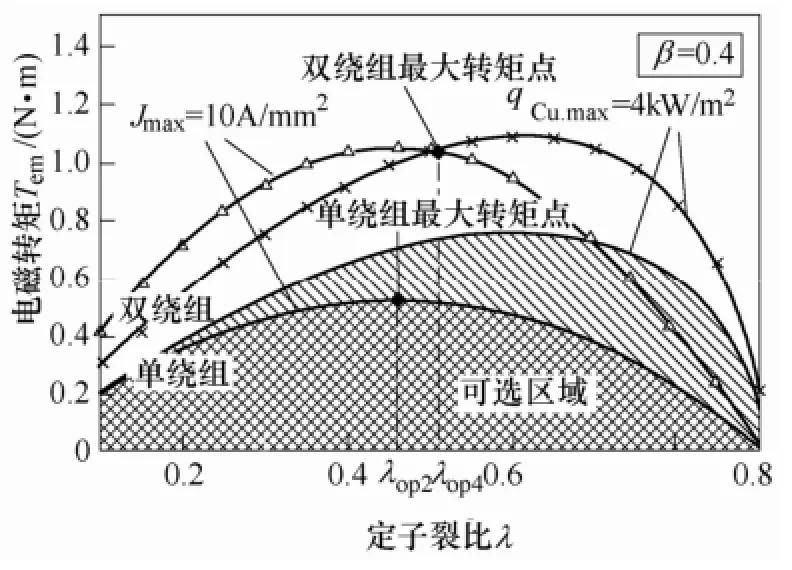
图11　限定qCu.max=4kW/m2、Jmax=10A/mm2， DRBLDCM的最优定子裂比Fig.11　Optimal split ratio of DRBLDCM when qCu.max=4kW/m2and Jmax=10A/mm2

DRBLDCM最优定子裂比的选取原则如下：

（1）对于冷备份单绕组工作方式，λop1、λop2和λop3值处于中间的为最佳定子裂比。例如：图9中λop2＜λop3＜λop1，则λop3为最佳定子裂比；图10中λop2＜λop1＜λop3，则λop1为最佳定子裂比。

（2）对于热备份双绕组工作方式，λop1、λop2和λop4值处于中间的为最佳定子裂比。例如：图9中λop2＜λop1＜λop4，则λop1为最佳定子裂比；图11中λop2＜λop4＜λop1，则λop4为最佳定子裂比。

4　有限元及实验验证

4.1有限元仿真验证

样机有限元仿真参数：Bmax=1.5T，β =0.37，qCu.max=4.2kW/m2，Jmax=15A/mm2（其他参数见表1）。

冷备份单绕组电磁转矩与定子裂比关系曲线的有限元仿真及解析计算结果如图12所示。仿真模型考虑了槽口高度，使电磁转矩仿真值小于解析值。分别限制铜耗密度和电流密度，有限元与解析计算所得最优定子裂比相同；同时限制铜耗密度和电流密度，有限元值为0.56，小于解析值0.57。

图12　单绕组Tem-λ 曲线的有限元仿真验证Fig.12　FEA verification of relationship between Temand λ with single coil operating

双绕组电磁转矩与定子裂比关系有限元仿真及解析计算结果如图13所示。双绕组运行绕组间磁动势会相互影响，使其电磁转矩小于单绕组的2倍和2倍；最优定子裂比仿真值与解析值相同，均为0.63。

图13　双绕组Tem-λ 曲线的有限元仿真验证Fig.13　FEA verification of relationship between Temand λ with dual coil operating

4.2实验验证

考虑电机体积、散热条件、绝缘材料和工作制等因素，限定样机qCu.max=4.2kW/m2、Jmax=15A/mm2。样机采用冷备份方式，参照本文方法，选择定子裂比为0.57（见图12），试制出样机，样机实物如图14所示，主要设计参数见表2。

搭建如图15所示实验测试平台，通过改变配重调节电机负载；利用功率分析仪（WT3000）测试电机转速、电流、电压和铜耗等参数。根据测得电流和已知导线截面积计算出电流密度；由测得的电机输入功率、转速和铜耗计算出电磁转矩。测试结果见表3，电磁转矩测试值与计算值相差9.3%，与仿真值相差6.9%。测试结果与理论分析和有限元仿真结果一致，结合4.1节有限元仿真结果，可证明采用所提优化方法可使电磁转矩得到充分提升。

本文方法基于理想模型，未考虑端部、铁耗、铁心饱和、槽口高度和漏磁等因素的影响，计算最优定子裂比与实际值相比存在一定误差。因项目要求，未试制热备份方式样机，未能开展相应实验。

图14　实物样机Fig.14　Practicality phototype

表2　实物样机主要设计参数Tab.2　Main parameters of the practicality prototype

图15　样机测试平台Fig.15　Experimental device for the prototype

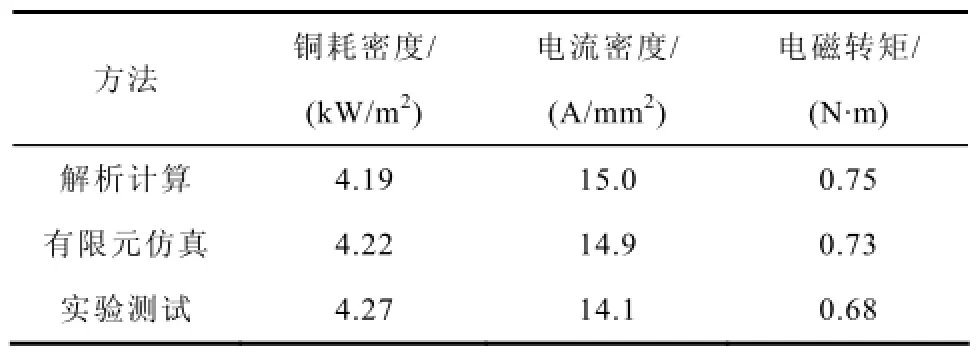
表3　样机测试结果及与仿真、解析计算结果的对比Tab.3 Testing results of the DRBLDCM prototype and comparison with simulation and calculation results

5　结论

本文在DRBLDCM外形尺寸一定条件下，针对热备份和冷备份方式，通过限制铜耗密度和电流密度以限制电机发热，以发热限制为电磁转矩边界，根据定子裂比、电磁转矩、铜耗密度、电流密度间的关系，推导得出两种备份方式电磁转矩最大对应最优定子裂比的表达式。分析表明，最优定子裂比受极对数和磁通密度系数影响；冷备份与热备份的最优定子裂比可能不同，取决于发热限制。有限元仿真及实验结果验证了理论分析的正确性，证明本文所提定子裂比优化方法可在限制发热条件下充分提升DRBLDCM的转矩。

［1］ 罗战强， 梁得亮. 双余度机电作动伺服系统数学模型与特性［J］. 电工技术学报， 2014， 29（1）： 165-173. Luo Zhanqiang， Liang Deliang. Mathematical model and characteristics on dual-redundancy electro- mechanical actuation servo system［J］. Transactions of China Electrotechnical Society， 2014， 29（1）： 165-173.

［2］ 罗战强， 梁得亮. 新型双余度永磁无刷电机稳态特性的等效磁路模型［J］. 电工技术学报， 2014， 29（5）： 84-92. Luo Zhanqiang， Liang Deliang. Equivalent magnetic circuit analysis model of the steady state charac- teristics for the novel dual-redundancy permanent magnet brushless machine［J］. Transactions of China Electrotechnical Society， 2014， 29（5）： 84-92.

［3］ 马瑞卿， 刘卫国， 解恩. 双余度无刷电动机位置伺服系统仿真与试验［J］. 中国电机工程学报， 2008， 28（18）： 98-103. Ma Ruiqing， Liu Weiguo， Xie En. Simulation and test of position servo system based on dual-redundancy BLDCM［J］. Proceedings of the CSEE， 2008， 28（18）： 98-103.

［4］ 罗玲， 刘卫国， 窦满峰， 等. 稀土永磁无刷直流电动机绕组嵌放对磁势的影响［J］. 中国电机工程学报， 2010， 30（9）： 86-91. Luo Ling， Liu Weiguo， Dou Manfeng， et al. Effects of armature windings embedding methods on magneto-motive force of rare earth permanent magnet brushless DC motor［J］. Proceedings of the CSEE， 2010， 30（9）： 86-91.

［5］ 付朝阳， 刘景林， 张晓旭. 双余度无刷直流电机匝间短路故障诊断［J］. 电工技术学报， 2014， 29（1）： 104-109. Fu Zhaoyang， Liu Jinglin， Zhang Xiaoxu. Research on inter-turn short circuit fault diagnosis of dual redundancy permanent magnet brushless DC motor［J］. Transactions of China Electrotechnical Society， 2014， 29（1）： 104-109.

［6］ 张超， 夏立， 吴正国， 等. 同步发电机转子绕组匝间短路故障特征传递规律［J］. 电力系统保护与控制， 2011， 39（14）： 52-57. Zhang Chao， Xia Li， Wu Zhengguo， et al. Transfer law of fault characteristics of interturn short circuit in synchronous generator rotor winding［J］. Power System Protection and Control， 2011， 39（14）： 52-57.

［7］ 何山， 王维庆， 张新燕， 等. 双馈风力发电机多种短路故障电磁场仿真研究［J］. 电力系统保护与控制， 2013， 41（12）： 41-46. He Shan， Wang Weiqing， Zhang Xinyan， et al. Simulation study of multiple short-circuit fault electro- magnetic field about DFIG in wind power［J］. Power System Protection and Control， 2013， 41（12）： 41-46.

［8］ 罗建锋， 唐轶， 陈奎， 等. 基于发热-散热积累模型的电动机过载保护研究［J］. 电力系统保护与控制， 2010， 38（3）： 95-98. Luo Jianfeng， Tang Yi， Chen Kui， et al. Study on motor over-load protection based on heat accumu- lation-emission model［J］. Power System Protection and Control， 2011， 38（3）： 95-98.

［9］ Reichert T， Nussbaumer T， Kolar J W. Split ratio optimization for high-torque PM motors considering global and local thermal limitations［J］. IEEE Transa- ctions on Energy Conversion， 2013， 28（3）： 493-501.

［10］ Galea M， Gerada C， Raminosoa T， et al. A thermal improvement technique for the phase windings of electrical machines［J］. IEEE Transactions on Industry Application， 2012， 48（1）： 79-87.

［11］ 孔晓光， 王凤翔， 邢军强. 高速永磁电机的损耗计算与温度场分析［J］. 电工技术学报， 2012， 27（9）： 166-173. Kong Xiaoguang， Wang Fengxiang， Xing Junqiang. Losses calculation and temperature field analysis of high speed permanent magnet machines［J］. Transa- ctions of China Electrotechnical Society， 2012， 27（9）： 166-173.

［12］ Pang Y， Zhu Z Q， Howe D. Analytical determination of optimal split ratio for permanent magnet brushless motors［J］. IEE Proceedings Electric Power Appli- cations， 2006， 153（1）： 7-13.

［13］ Chu W Q， Zhu Z Q， Chen J T. Simplified analytical optimization and comparison of torque densities between electrically excited and permanent-magnet machines［J］. IEEE Transactions on Industry Electronics， 2014， 61（9）： 5000-5011.

［14］ Wu L J， Zhu Z Q， Chen J T， et al. Optimal split ratio in fractional-slot interior permanent-magnet machines with non-overlapping windings［J］. IEEE Transa- ctions on Magnetics， 2010， 46（5）： 1235-1242.

［15］ Sheng Y， Zhu Z Q. Analytical prediction of optimal split ratio for fractional-slot external rotor PM brush- less machines［J］. IEEE Transactions on Magnetics， 2011， 47（10）： 4187-4190.

［16］ Ede J D， Zhu Z Q， Howe D. Optimal split ratio for high-speed permanent magnet brushless DC motors［C］. International Conference on Electrical Machines and Systems， Shenyang， China， 2001： 909-912.

李全武 男，1986年生，博士研究生，研究方向为永磁电机设计。

窦满峰 男，1967年生，教授，博士生导师，研究方向为永磁电机的设计及驱动控制。

Split Ratio Optimization Method for Dual-Redundancy Brushless DC Motors Considering Thermal Limitations

Li Quanwu Dou Manfeng
（Northwestern Polytechnical University Xi'an 710072 China）

A novel split ratio optimization method used in aviation electromechanical actuator is proposed to increase the torque of dual redundancy brushless DC motor （DRBLDCM）， where volume and reliability can be ensured. Global thermal limitation of motor is set by limiting copper loss density， and local thermal limitation of coil is set by limiting current density. Expression of optimal split ratio for warm spare and cold spare is presented by analyzing the relationship between spilt ratio and electromagnetic torque. The analytical optimal split ratio value is verified by finite element analysis （FEA）， and the error is less than 2%. Testing value of electromagnetic torque is 9.3% less than the analytical value. FEA and testing results proved that the method can increase the torque of DRBLDCM with limited size and heat.

Dual-redundancy， brushless DC motors， split ratio， thermal limitation

TM351

中国科学院光电研究院雏鹰计划资助项目（2012005）。

2014-10-27 改稿日期 2015-01-13